業務分析・データ利活用(全82問中6問目)
No.6解説へ
製品X,Yを1台製造するのに必要な部品数は,表のとおりである。製品1台当たりの利益がX,Yともに1万円のとき,利益は最大何万円になるか。ここで,部品Aは120個,部品Bは60個まで使えるものとする。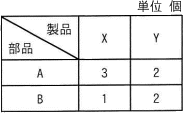

出典:令和6年春期 問75
- 30
- 40
- 45
- 60
正解 ウ問題へ
広告
解説
製品1台当たりの利益は同額であるため、部品を余すことなく使い、最も多く作ることのできる組合せが部品の最適配分となります。1次式を満たす変数の値の中で式を最大化または最小化する値を求める方法として「線形計画法」があります。
この問題も製品Xの生産数をx、製品Yの生産数をyとして、"x+yの最大化"を目的関数とする線形計画法の問題として捉えることができます。部品A・Bを使い切るときのxとyの値は連立方程式を使って以下のように求めます。
{3x+2y=120 …①
{x+2y=60 …②
①-②をして、
2x=60
x=30 …③
②に③を代入して、
30+2y=60
2y=30
y=15
計算結果より、製品Xを30個、製品Yを15個生産したときに、すべての部品を使い切り、計45個の製品を生産できることがわかります。製品1台当たりの利益は1万円ですから、利益の最大額は「ウ」の45万円となります。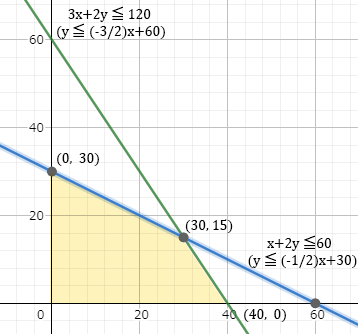
この問題も製品Xの生産数をx、製品Yの生産数をyとして、"x+yの最大化"を目的関数とする線形計画法の問題として捉えることができます。部品A・Bを使い切るときのxとyの値は連立方程式を使って以下のように求めます。
{3x+2y=120 …①
{x+2y=60 …②
①-②をして、
2x=60
x=30 …③
②に③を代入して、
30+2y=60
2y=30
y=15
計算結果より、製品Xを30個、製品Yを15個生産したときに、すべての部品を使い切り、計45個の製品を生産できることがわかります。製品1台当たりの利益は1万円ですから、利益の最大額は「ウ」の45万円となります。

広告