令和4年春期試験午後問題 問3
問3 プログラミング
⇱問題PDF
パズルの解答を求めるプログラムに関する次の記述を読んで,設問1~3に答えよ。
パズルの解答を求めるプログラムに関する次の記述を読んで,設問1~3に答えよ。
広告
太線で3×3の枠に区切られた9×9のマスから成る正方形の盤面に,1~9の数字を入れるパズルの解答を求めるプログラムを考える。このパズルは,図1に示すように幾つかのマスに数字が入れられている状態から,数字の入っていない各マスに,1~9のうちのどれか一つの数字を入れていく。このとき,盤面の横1行,縦1列,及び太線で固まれた3×3の枠内の全てにおいて,1~9の数字が一つずつ入ることが,このパズルのルールである。パズルの問題例を図1に,図1の解答を図2に示す。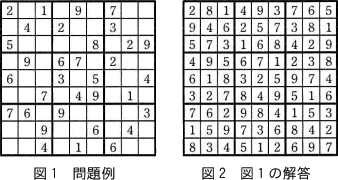 このパズルを解くための方針を次に示す。
このパズルを解くための方針を次に示す。
〔パズルを解く手順〕
この手順をプログラムに実装するために,9×9の盤面を次のデータ構造で表現することにした。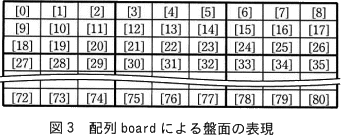 〔ルールのチェック方法〕
〔ルールのチェック方法〕
パズルのルールにのっとっているかどうかのチェックでは,数字を入れたマスが含まれる横1行の左端のマス,縦1列の上端のマス,3x3の枠内の左上端のマスを特定し,行,列,枠内のマスに既に格納されている数字と,入れた数字がそれぞれ重複していないことを確認する。このチェックを"重複チェック"という。
〔解法のプログラム〕
プログラムで使用する配列,関数,変数及び定数の一部を表1に示す。なお,表1の配列及び変数は大域変数とする。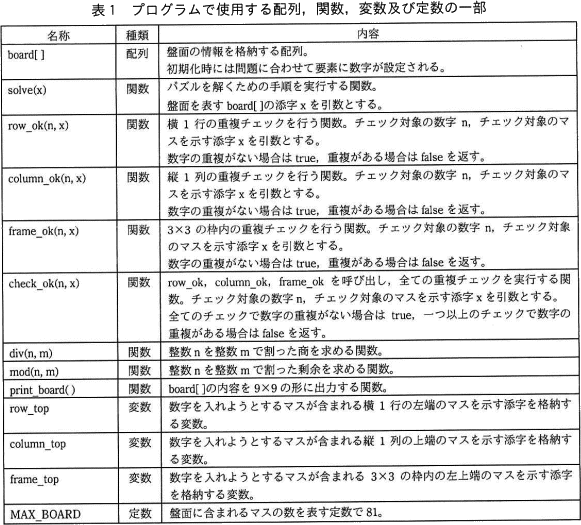 解法のプログラムのメインプログラムを図4に,関数 solve のプログラムを図5に,重複チェックを行うプログラムの一部を図6に示す。
解法のプログラムのメインプログラムを図4に,関数 solve のプログラムを図5に,重複チェックを行うプログラムの一部を図6に示す。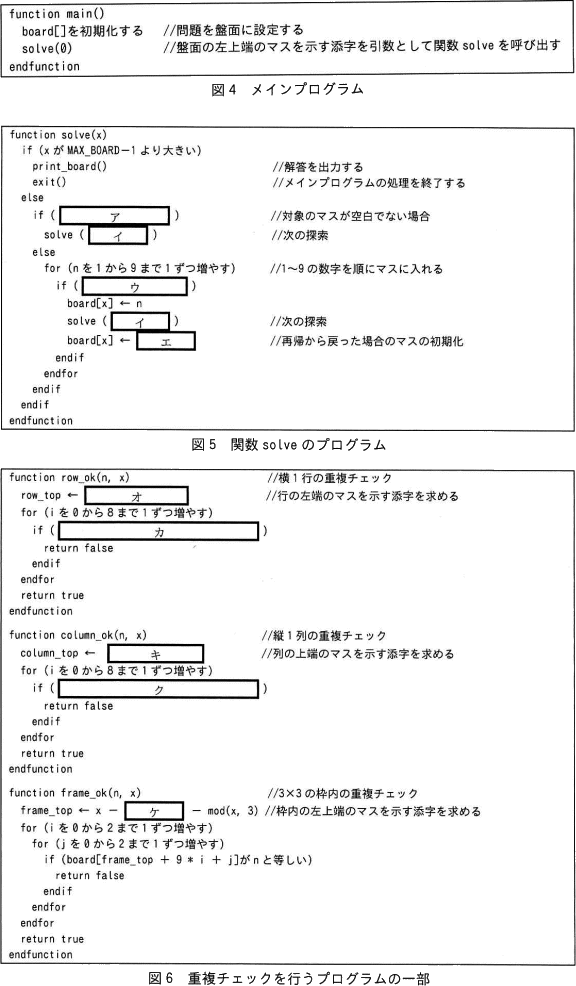 〔プログラムの改善〕
〔プログラムの改善〕
解法のプログラムは深さ優先探索であり,探索の範囲が広くなるほど,再帰呼出しの回数が指数関数的に増加し,重複チェックの実行回数も増加する。
そこで,重複チェックの実行回数を少なくするために,各マスに入れることができる数字を保持するためのデータ構造Zを考える。データ構造Zは盤面のマスの数×9の要素をもち,添字xは0から,添字nは1から始まる2次元配列とする。Z[x][n]は,ゲームのルールにのっとってboard[x]に数字nを入れることができる場合は要素に1を,できない場合は要素に0を格納する。データ構造Zの初期化処理と更新処理を表2のように定義した。
なお,データ構造Zは大域変数として導入する。 〔パズルを解く手順〕の(1)の前にデータ構造Zの初期化処理を追加し,〔パズルを解く手順〕の(2)~(5)を次の(2)~(4)のように変更した。
〔パズルを解く手順〕の(1)の前にデータ構造Zの初期化処理を追加し,〔パズルを解く手順〕の(2)~(5)を次の(2)~(4)のように変更した。

方針:数字が入っていない空白のマスに,1~9の数字を入れて,パズルのルールにのっとって全部のマスを埋めることができる解答を探索する。
この方針に沿ってパズルを解く手順を考える。〔パズルを解く手順〕
- 盤面の左上端から探索を開始する。マスは左端から順に右方向に探索し,右端に達したら一行下がり,左端から順に探索する。
- 空白のマスを見つける。
- (2)で見つけた空白のマスに,1~9の数字を順番に入れる。
- 数字を入れたときに,その状態がパズルのルールにのっとっているかどうかをチェックする。
(4-1) ルールにのっとっている場合は,(2)に進んで次の空白のマスを見つける。
(4-2) ルールにのっとっていない場合は,(3)に戻って次の数字を入れる。このとき,入れる数字がない場合には,マスを空白に戻して一つ前に数字を入れたマスに戻り,(3)から再開する。 - 最後のマスまで数字が入り,空白のマスがなくなったら,それが解答となる。
この手順をプログラムに実装するために,9×9の盤面を次のデータ構造で表現することにした。
- 9×9の盤面を81個の要素をもつ1次元配列 board で表現する。添字は0から始まる。各要素にはマスに入れられた数字が格納され,空白の場合は0を格納する。

パズルのルールにのっとっているかどうかのチェックでは,数字を入れたマスが含まれる横1行の左端のマス,縦1列の上端のマス,3x3の枠内の左上端のマスを特定し,行,列,枠内のマスに既に格納されている数字と,入れた数字がそれぞれ重複していないことを確認する。このチェックを"重複チェック"という。
〔解法のプログラム〕
プログラムで使用する配列,関数,変数及び定数の一部を表1に示す。なお,表1の配列及び変数は大域変数とする。


解法のプログラムは深さ優先探索であり,探索の範囲が広くなるほど,再帰呼出しの回数が指数関数的に増加し,重複チェックの実行回数も増加する。
そこで,重複チェックの実行回数を少なくするために,各マスに入れることができる数字を保持するためのデータ構造Zを考える。データ構造Zは盤面のマスの数×9の要素をもち,添字xは0から,添字nは1から始まる2次元配列とする。Z[x][n]は,ゲームのルールにのっとってboard[x]に数字nを入れることができる場合は要素に1を,できない場合は要素に0を格納する。データ構造Zの初期化処理と更新処理を表2のように定義した。
なお,データ構造Zは大域変数として導入する。

- 空白のマスを見つける。
- データ構造Zを参照し,(2)で見つけた空白のマスに入れることができる数字のリストを取得し,リストの数字を順番に入れる。
(3-1) 入れる数字がある場合,①処理Aを行った後,マスに数字を入れる。その後,データ構造Zの更新処理を行い,(2)に進んで次の空白のマスを見つける。
(3-2) 入れる数字がない場合,マスを空白に戻し,②処理Bを行った後,一つ前に数字を入れたマスに戻り,戻ったマスで取得したリストの次の数字から再開する。 - 最後のマスまで数字が入り,空白のマスがなくなったら,それが解答となる。
広告
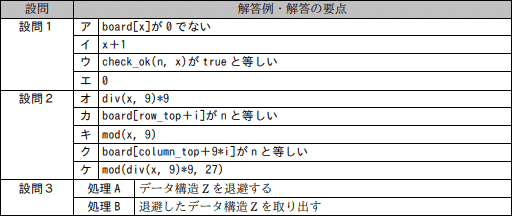
設問1
図5中のア~エに入れる適切な字句を答えよ。
解答例・解答の要点
ア:board[x]が0でない
イ:x+1
ウ:check_ok(n, x)がtrueと等しい
エ:0
イ:x+1
ウ:check_ok(n, x)がtrueと等しい
エ:0
解説
本問で扱っているパズルは、"数独"や"ナンプレ(ナンバープレース)"と呼ばれるものです。もし文章だけではルールがわかりにくい場合は、実際にプレイしてみるとイメージしやすいでしょう。解説の便宜上、図5のプログラムに行番号を振っておきます。
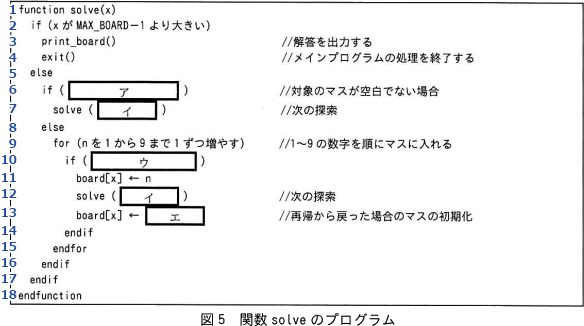
空欄にはif文の条件式が入ります。6行目のコメントに「//対象のマスが空白でない場合」とあるので、これを表現できるような条件式を考えます。
〔盤面の表現〕を読むと、9×9の盤面は全81個から成る1次元配列 board で表現され、空白の場合は要素に0を格納するとあります。表1の solve(x) の説明に「盤面を表す board[] の添字xを引数とする」とあるため、関数 solve 内において現在対象となっているマスはxであり、それに対応する配列 board 上の要素は board[x] で参照することができます。
対象のマスが空白でないときに条件式がtrueを返すようにしたいので、適切な条件式はboard[x]が0でないとなります。
∴ア=board[x]が0でない
〔イについて〕
空欄は関数 solve の引数です。7行目のコメントに「//次の探索」とあるように、対象のマスが空白でない場合には、空白のマスが見つかるまで探索対象を次のマスに移す操作を行うことになります。したがって、[イ]に入るのは次に探索するマスの添字となります。
〔パズルを解く手順〕(1)に「マスは左端から順に右方向に探索し,右端に達したら一行下がり,左端から順に探索する」とあることから、次に探索するマスとは、探索しているマスの右隣、右端を探索している場合は一行下の左端となります。図3が示すとおり盤面の情報は一次元配列の board に格納されていて、xの次のマスは単純にx+1となっています。
したがって、関数 solve の引数として指定するのはx+1となります。
∴イ=x+1
〔ウについて〕
空欄にはif文の条件式が入ります。[ウ]がある10行目にはコメントがないので、分岐後の処理から条件式を推測します。
分岐後の処理を見ると、11行目で添字xのマスに数字を入れ、直後の12行目では次のマスの探索を行っています。ここで〔パズルを解く手順〕の内容と照らし合わせると、この「数字を入れた後に次のマスを探索する」に該当する手順は(4-1)とわかります。これより、[ウ]には手順(4-1)の実行条件、すなわち「数字を入れたときに、その状態がパズルのルールにのっとっている」を満たす場合にtrueとなる条件式が入ると判断できます。
ここで、パズルのルールは本文中で「盤面の横1行,縦1列,及び太線で固まれた3×3の枠内の全てにおいて,1~9の数字が一つずつ入る(=数字の重複がない)」と説明されています。このルールをチェックする処理は1行で書き表せないほど複雑ですが、表1を見ると、以下の3つを全部まとめて呼び出す関数 check_ok が用意されていることがわかります。
- 横1行の重複チェックを行う関数 row_ok
- 縦1行の重複チェックを行う関数 colmun_ok
- 3×3の枠内の重複チェックを行う関数 frame_ok
関数 check_ok(n, x) の説明には「横1行・縦1列・3×3の枠内それぞれで重複が"ない"場合にtrueを返す」とあるので、関数 check_ok がtrueを返せば「パズルのルールにのっとっている」という条件を満たすことになります。引数nはチェック対象の数字なので現在マスに入れようとしている数字を保持するループ変数のn、引数xはチェック対象マスの添字なので現在対象となっているマスに対象となっているマスの添字を保持するxを指定します。したがって、[ウ]に当ては条件式はcheck_ok(n, x)がtrueと等しいとなります。
∴ウ=check_ok(n, x)がtrueと等しい
〔エについて〕
空欄に入るのは、board[x](探索対象のマス)に代入する値です。[エ]が含まれる行のコメントには「//再帰から戻った場合のマスの初期化」とあります。
関数 solve は再帰構造になっていて、10行目のif文がtrueとなった場合には対象のマスに数字を入れて次のマスの探索に移ります。その後、次のマスに何らかの数字が入ればさらに次のマスの探索に移りますが、何の数字も入らない場合には関数 solve は何もせずに呼出し元に帰る(再帰から戻る)ことになります。したがって、solve の次に位置する13行目の処理は、次のマスに何の数字も入らなかったときに行われる処理ということになります。
今そのマスに入れいている数字では次のマスに入る数字がないので、先ほど board[x] に入れた数字を初期化する必要があります。仮の数字が入ったままだと重複チェックが正しく動作しないためです。マスの初期状態は空白、空白は0で表すので、board[x] に代入すべきは0が適切です。
∴エ=0
広告
設問2
図6中のオ~ケに入れる適切な字句を答えよ。
解答例・解答の要点
オ:div(x, 9)*9
カ:board[row_top+i]がnと等しい
キ:mod(x, 9)
ク:board[column_top+9*i]がnと等しい
ケ:mod(div(x, 9)*9, 27)
カ:board[row_top+i]がnと等しい
キ:mod(x, 9)
ク:board[column_top+9*i]がnと等しい
ケ:mod(div(x, 9)*9, 27)
解説
解説の便宜上、図6のプログラムに行番号を振っておきます。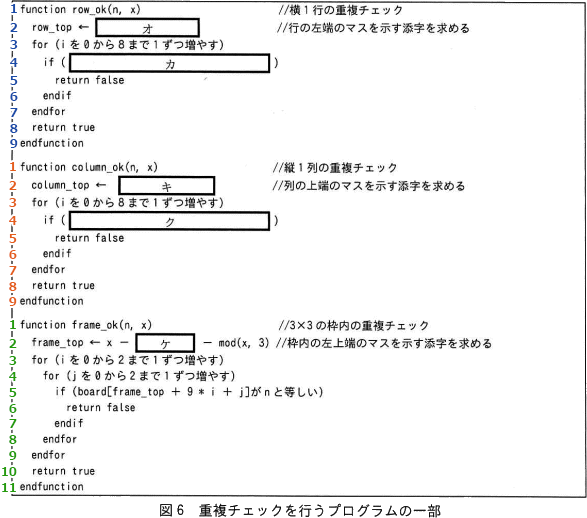
対象のマスを示す添字xから、その行の左端のマスを示す添字を求める式が入ります。
行の左端マスの添字は、上から順に0,9,18,…,72と9の倍数になっており、具体的には、xと左端のマスの添字は以下のように対応しています。
- 0~8の場合 → 0
- 9~17の場合 → 9
- …
- 72~80の場合 → 72
xからxを9で割った余りを引いても求められるので、x-mod(x, 9)も解答として可です。
∴オ=div(x, 9)*9
〔カについて〕
表1より、関数 row_ok は横1行の重複チェックを行う関数で、数字の重複がある場合にはfalseを返すことがわかります。動作としては、for文でiを1ずつ増やすことで行の左端から1マスずつチェックしていき、nと同じ数があった場合には"重複あり"と判定しています。if文が真のときにはfalseを返しているので、空欄に入るのは、nと同じ数字が見つかったときにtrueとなる条件式です。
行の左端を示すマスは変数 row_top を用いて board[row_top]、左端から1つ右のマスは board[row_top+1]、その1つ右のマスは board[row_top+2] というように表せるので、for文中で現在重複チェックしているマスは board[row_top+i] と表すことができます。
board[row_top+i] にnが格納されている場合には"重複あり"ということになるので、条件式としてはboard[row_top+i]がnと等しいが適切です。
∴カ=board[row_top+i]がnと等しい
〔キについて〕
対象のマスを示す添字xより、その列の上端のマスを示す添字を求める式が入ります。具体的には、xと上端のマスの添字は以下のように対応しています。
- 0,9,18,27,…,72の場合 → 0
- 1,10,19,28,…,73の場合 → 1
- …
- 8,17,26,35,…,80の場合 → 8
∴キ=mod(x, 9)、別解:x-div(x, 9)*9
〔クについて〕
表1より、関数 colmun_ok は縦1列の重複チェックを行う関数で、数字の重複がある場合にはfalseを返すことがわかります。関数 row_ok と同様にループ変数 i を使って縦1列をチェックしていき、値の重複があればfalseを返す仕様です。
添字の値は行が1つ下になるたびに9増えるので、列の上端を示すマスは変数 column_top を用いて board[column_top]、上端から1つ下のマスは board[column_top+9]、その1つ下のマスは board[row_top+18] ということになります。+9、+18の部分をiを使って表現すると「9*i」となるので、for文中で現在重複チェックしているマスは board[column_top+i*9] と表すことができます。
board[column_top+i*9] にnが格納されている場合には"重複あり"ということになるので、条件式としてはboard[column_top+i*9]がnと等しいが適切です。
∴ク=board[column_top+9*i]がnと等しい
〔ケについて〕
対象のマスを示す添字xより、その枠内の左上端のマスを示す添字を求める式が入ります。
関数 frame_ok の2行目には既にxから mod(x, 3) を引く式が記されているので、 まずはこの処理の意味について考えます。
チェック対象の添字xから mod(x, 3) を引いた値は、チェック対象のマスが、
- 1,4,7列目にある場合は、対象のマス自身の添字
- 2,5,8列目にある場合は、対象の1つ左のマスの添字
- 3,6,9列目にある場合は、対象の2つ左のマスの添字
したがって、[ケ]には「列の位置を変えずに、行を3×3の枠内の上端の位置」にするために引くべき値を入れればよいです。具体的には、チェック対象のマスが、
- 1,4,7行目にある場合は、そのまま(0を引く)
- 2,5,8行目にある場合は、9を引く
- 3,6,9行目にある場合は、18を引く
上記の「引くべき値」は、1,2,3行目の場合には div(x, 9)*9 で求められますが、4~9行目の場合はこれでは不適切です。ここで、4~6行目では「div(x, 9)*9」と「引くべき値」の差が27、7~9行目では「div(x, 9)*9」と「引くべき値」の差が54になっているので、「div(x, 9)*9」を27で割った剰余を使う、すなわち「mod(div(x, 9)*9, 27)」が引くべき値を求める式ということになります。
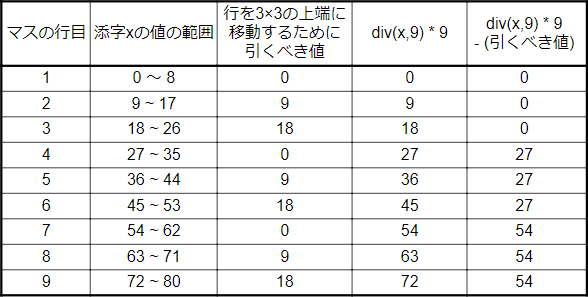
∴ケ=mod(div(x, 9)*9, 27)
※別解が多数考えられるため、別の解答が正しいか確かめたい場合はプログラムや表計算ソフト等で確認してみてください。
<別解例>
mod(div(x, 9), 3)*9
div(mod(x, 27), 9)*9
div(x, 9)*9 - div(x, 27)*27 等
広告
設問3
解答例・解答の要点
A:データ構造Zを退避する (11文字)
B:退避したデータ構造Zを取り出す (15文字)
B:退避したデータ構造Zを取り出す (15文字)
解説
データ構造Zの更新処理では、マスに数字を入れたときにそのマスに関連するマスの数字の要素を0にすることはできますが、逆に0を1に戻すことはできません。つまり、マスに数字を入れた場合、データ構造Zの内容は不可逆となってしまうということがポイントです。入れる数字がなくマスを空白にして前に戻る場合、そのマスに数字を入れる前の状態のデータ構造Zが必要になりますが、次のマスの処理で更新されているデータ構造Zは巻き戻し不可なので使うことはできません(データ構造は大域変数)。また、データ構造Zを巻き戻すには盤面に対して戻った都度重複チェックを行う必要があり、本文で記されている「重複チェックの実行回数を少なくする」という方針に適しません。これを回避するために、数字を入れて次のマスの探索に移る前に、数字を入れる前のデータ構造Zを関数内の一時変数として保持しておく必要があります。
数字を入れる前にデータ構造Zを退避しておき、マスを空白にして一つ前に戻った後に退避したデータ構造Zを取り出せば適切に処理を進めることができます。したがって、[処理A]はデータ構造Zを退避する、[処理B]は退避したデータ構造Zを取り出すとなります。
∴処理A=データ構造Zを退避する
処理B=退避したデータ構造Zを取り出す
広告
広告