平成22年秋期試験午後問題 問2
問2 プログラミング
⇱問題PDF
構文解析に関する次の記述を読んで，設問1～4に答えよ。
構文解析に関する次の記述を読んで，設問1～4に答えよ。
広告
宣言部と実行部からなる図1のような記述をするプログラム言語がある。その構文規則を，括弧記号で表記を拡張したBNFによって，図2のように定義した。
図2において，引用符「‘」と「’」で固まれた記号や文字列，＜数＞，及び＜識別子＞は終端記号を表す。そのほかの「＜」と「＞」で固まれた名前は非終端記号を表す。＜数＞は1文字以上の数字の列を表し，＜識別子＞は英字で始まる1文字以上の英字又は数字からなる文字列を表す。
また，A｜B はAとBのいずれかを選択することを表し，{A} はAを0回以上繰り返すことを表す。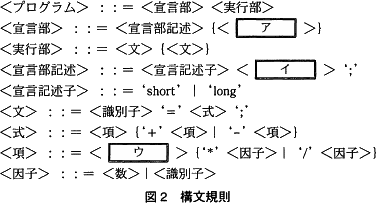
例えば，図1の最初の行 "short aa ;" は，図2の＜宣言部記述＞の定義に従っていて，＜宣言記述子＞と‘short’，＜イ＞ と‘aa’ 更に‘;’同士がそれぞれ対応していることが分かる。
〔字句解析関数の定義〕
プログラム記述が図2の構文規則に従っているかどうかを検査するプログラムを作成するために，字句を先頭から順番に抽出し，その種類を判定する関数 gettoken() を定義する。ここでいう字句とは，構文規則における終端記号である。字句と字句は，空白や改行文字で区切られている。空白や改行文字は，字句そのものには含まれない。字句の種類と関数 gettoken() の戻り値の対応を表に示す。
なお，‘short’と‘long’は＜識別子＞には含まれない。また，いずれの終端記号にも該当しない字句やプログラム記述の終わりを検出した場合の戻り値も定義する。
〔構文解析プログラム〕
図3は，図2の構文規則に従って，＜文＞及び＜式＞の構文を検査するプログラムである。プログラムの前提条件を次に示す。
また，A｜B はAとBのいずれかを選択することを表し，{A} はAを0回以上繰り返すことを表す。
〔字句解析関数の定義〕
プログラム記述が図2の構文規則に従っているかどうかを検査するプログラムを作成するために，字句を先頭から順番に抽出し，その種類を判定する関数 gettoken() を定義する。ここでいう字句とは，構文規則における終端記号である。字句と字句は，空白や改行文字で区切られている。空白や改行文字は，字句そのものには含まれない。字句の種類と関数 gettoken() の戻り値の対応を表に示す。
なお，‘short’と‘long’は＜識別子＞には含まれない。また，いずれの終端記号にも該当しない字句やプログラム記述の終わりを検出した場合の戻り値も定義する。
図3は，図2の構文規則に従って，＜文＞及び＜式＞の構文を検査するプログラムである。プログラムの前提条件を次に示す。
- ＜文＞，＜式＞及び＜項＞の構文解析を行う関数をそれぞれ bun()，shiki() 及び kou() とする。これらの関数の戻り値は，構文が正しい場合は 0，エラーが検知された場合は－1である。
- 構文解析を行う各関数実行開始時の変数 token の値は，検査の対象となる文字列の最初の字句に対する関数 gettoken() の戻り値である。
広告
設問1
図2中のア～ウに入れる適切な非終端記号又は終端記号の名前を答えよ。
解答例・解答の要点
ア：宣言部記述
イ：識別子
ウ：因子
イ：識別子
ウ：因子
解説
BNFとは、プログラム等の文法を定義する規則のことです。例えば「＜プログラム＞::=＜宣言部＞＜実行部＞」は、「＜プログラム＞は＜宣言部＞と＜実行部＞をつなげたものである」という意味になります。
また、本問で解答する「非終端記号又は終端記号」とは、本文より「非終端記号」が図2の「＜＞」で囲まれた名前(プログラム、宣言部等)、「終端記号」が＜数＞および＜識別子＞です。
以上を踏まえて、イ→ア→ウの順で解説を進めます。
〔イについて〕
「図1の最初の行 "short aa ;" は，図2の＜宣言部記述＞の定義に従っていて，＜宣言記述子＞と'short'，＜イ＞ と'aa' 更に';'同士がそれぞれ対応している」からわかるように、[イ]は'aa'に対応するものです。本文中に「＜識別子＞は英字で始まる1文字以上の英字又は数字からなる文字列を表す」とあることから、'aa'は＜識別子＞です。よって、[イ]には「識別子」が当てはまります。
∴イ＝識別子
〔アについて〕
[ア]は＜宣言部記述＞のあとに0回以上繰り返されるものです。図1の＜宣言部＞について考えると、先程確認したように1行目が＜宣言部記述＞ですから、2～3行目は[ア]が繰り返されたものと推測できます。
ここで、2・3行目に現れる'long'は、図2の5行目より＜宣言記述子＞、そして'b1'および'c'はどちらも＜識別子＞です。これより、2・3行目はそれぞれ＜宣言部記述＞の定義に合致します。＜宣言部記述＞を2回繰り返しているとみなせるので、[ア]には「宣言部記述」が当てはまります。
＜宣言部＞は1つ以上の＜宣言部記述＞から成るという意味です。
∴ア＝宣言部記述
〔ウについて〕
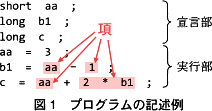
＜項＞は[ウ]の後ろに0つ以上の「'*' ＜因子＞」または「'/' 因子」が続いたものなので、[ウ]は単独で＜項＞として扱えることがわかります。これをヒントに図1中で＜項＞を表す箇所に注目して考えていきます。
まず＜式＞の定義より、＜項＞は'+'および'-'の前後に現れることに着目します。図1のプログラムで'+'および'-'の前後に現れているのは、'aa'、'1'、'2 * b1'で、それぞれが＜項＞です。
∴ウ＝因子
広告
設問2
次のプログラム記述には，図2で示した構文規則に反するエラーが幾つか含まれている。構文規則に反するエラーを含む行の番号をすべて答えよ。
解答例・解答の要点
②，⑤
解説
- 'short'は＜宣言部記述子＞、'abc'は＜識別子＞です。
よって、①は「＜宣言部記述子＞＜識別子＞';'」と表すことができ、＜宣言部記述＞の定義に当てはまります。 - 'short'は＜宣言部記述子＞、'def'・'ghi'は＜識別子＞です。
よって、②は「＜宣言部記述子＞＜識別子＞＜識別子＞';'」と表すことができます。＜宣言部記述＞の定義には＜識別子＞は1個しか現れないので、②にあてはまる構文規則はありません。したがって、②はエラーとなります。 - 'long'は＜宣言部記述子＞、'mno'は＜識別子＞です。
よって、③は「＜宣言部記述子＞＜識別子＞';'」と表すことができ、＜宣言部記述＞の定義に当てはまります。 - 'abc'・'def'は＜識別子＞、'34'は＜数＞です。
よって、④は「＜識別子＞'='＜識別子＞'+'＜数＞';'」と表すことができます。これを構文規則に従って変換していくと、- ＜因子＞の定義より「＜識別子＞'='＜因子＞'+'＜因子＞';'」
- ＜項＞の定義より「＜識別子＞'='＜項＞'+'＜項＞';'」
- ＜式＞の定義より「＜識別子＞'='＜式＞';'」
- 'ghi'・'mno'は＜識別子＞、'2'は＜数＞です。
よって、⑤は「＜識別子＞'=''-'＜数＞'*'＜識別子＞';'」と表すことができます。これを構文規則に従って変換していくと、- ＜因子＞の定義より「＜識別子＞'=''-'＜因子＞'*'＜因子＞';'」
- ＜項＞の定義より「＜識別子＞'=''-'＜項＞';'」
- 'mno'・'abc'は＜識別子＞、'0'は＜数＞です。
よって、⑥は「＜識別子＞'='＜識別子＞'/'＜数＞';'」と表すことができます。これを構文規則に従って変換していくと、- ＜因子＞の定義より「＜識別子＞'='＜因子＞'/'＜因子＞';'」
- ＜項＞の定義より「＜識別子＞'='＜項＞';'」
- ＜式＞の定義より「＜識別子＞'='＜式＞';'」
※なお、ゼロ除算は大抵のプログラムで実行時エラーが発生しますが、今回は構文規則に反するかどうかのみを考えることに注意してください。 - 'xyz'・'def'は＜識別子＞、'7'は＜数＞です。
よって、⑦は「＜識別子＞'='＜識別子＞'-'＜数＞';'」と表すことができます。これを構文規則に従って変換していくと、- ＜因子＞の定義より「＜識別子＞'='＜因子＞'-'＜因子＞';'」
- ＜項＞の定義より「＜識別子＞'='＜項＞'-'＜項＞';'」
- ＜式＞の定義より「＜識別子＞'='＜式＞';'」
∴②，⑤
広告
設問3
図3中のエ，オに入れる適切な字句を答えよ。
解答例・解答の要点
エ：tokenと'='が等しい
オ：kou()と－1が等しい
オ：kou()と－1が等しい
解説
〔エについて〕[エ]が含まれている関数bun()は、＜文＞の構文解析を行う関数です。
検査の対象となる文字列が正常な＜文＞、すなわち「＜識別子＞'='＜式＞」となる場合を考えて、処理を順に追っていきます。解説の便宜上、プログラムに行番号を振っておきます。
2行目は変数 token との比較処理です。このときの変数 token の値について考えます。本文に「構文解析を行う各関数実行開始時の変数 token の値は，検査の対象となる文字列の最初の字句に対する関数 gettoken() の戻り値である」とあります。今回検査の対象として考えている「＜識別子＞'='＜式＞」の最初の字句は＜識別子＞ですから、表より変数 token の値は'I'です。これより、分岐先は3行目になります。反対に変数 token の値が'I'と異なれば（最初の字句が＜識別子＞でなければ）エラーとして終了します。
3行目では変数 token に値が代入されています。この値が何になるか考えます。代入元である関数 gettoken() は本文より「字句を先頭から順番に抽出し，その種類を判定」して返す関数です。よって、＜識別子＞の次の字句である'='に対応する戻り値、すなわち'='が変数 token に代入されます。
次に、2つ目の分岐処理(関数bun()の7～11行目)を追っていきます。
10行目にあるように、7行目の条件[エ]が偽の場合、-1を返して関数は終了します。本文より関数 bun() の戻り値は「エラーが検知された場合は-1」です。すなわち[エ]は「構文が正しい場合は真、間違っていた場合は偽」となるような条件となります。ここで、構文が正しい場合、7行目での変数 token の値は、1つ目の分岐処理で確認したように'='となっているはずです。これを元に条件を設定すればよいので、[エ]には「tokenと'='が等しい」が当てはまります。
∴エ＝tokenと'='が等しい
〔オについて〕
[オ]が含まれている関数shiki()は、＜式＞の構文解析を行う関数です。
[エ]と同様に、検査の対象となる文字列が正常な＜式＞、すなわち「＜項＞{'+'＜項＞|'-'＜項＞}」の形となっている場合を考えます。解説の便宜上、プログラムに行番号を振っておきます。
条件[オ]が真の場合、-1を返して関数が終了するので、[オ]は「構文が間違っている場合は真、正しい場合は偽」であるような条件です。ここで、正常な＜式＞であれば先頭の字句は必ず＜項＞であることから、[オ]に入る条件は「＜項＞の構文解析がエラーである」となります。＜項＞の構文解析を行う関数はkou()ですから、これを利用して条件を書けばよいです。関数kou()はエラーが検知された場合に-1を返すので、解答は「kou()と-1が等しい」となります。
∴オ＝kou()と－1が等しい
広告
設問4
"d = a * (3 + b) ;" のように，式の演算子の評価順序を明示的に記述するため，「(」及び「)」を使えるように構文規則を拡張したい。これについて，(1)，(2)に答えよ。
- 図2の構文規則の中の＜因子＞の行を，次のように書き換えた。カに入れる適切な字句を答えよ。
＜因子＞：：＝＜数＞｜＜識別子＞|‘(’カ‘)’ - この構文規則の拡張によって，関数 gettoken() も修正する必要がある。どのような修正が必要か，35字以内で述べよ。
解答例・解答の要点
- カ：＜式＞
- ・「(」と「)」に対してほかの字句とはそれぞれ別の戻り値を返す (30文字)
・( と ) の字句に対しそれぞれ ( と ) を返す (26文字)
解説
- [カ]は'('と')'で囲まれています。よって、問題文で例に上げられている"d = a * (3 + b) ;"の括弧内「3 + b」が[カ]に対応します。
「3 + b」を構文規則によって変換していくと、「3 + b」→「＜因子＞'+'＜因子＞」→「＜項＞'+'＜項＞」→「＜式＞」となるので、解答は「＜式＞」です。
【別解】
解答候補は、＜項＞、＜式＞、＜文＞になると思います。＜項＞は、'+'または'-'で繋がれた文字列を挿入できないので誤り、＜文＞は「＜識別子＞'='＜式＞」形式の代入文が挿入可能になってしまうので誤りです。"3 + b * 5 + 5"のような文字列を＜因子＞として扱うためには＜式＞である必要があります。
∴カ＝＜式＞ - 関数 gettoken() は、字句の種類を判定する関数でした。
今回、構文規則で「(」および「)」を使えるように拡張しますが、このままでは関数 gettoken() で「(」「)」が「いずれにも該当しない字句」として判定されてしまい、"?"が返ってきます。これだと適切な構文解析を行うことができません。
したがって、「(」と「)」それぞれに対して他の字句とは異なる戻り値を設定することで、「(」と「)」を識別できるようにする必要があります。解答としては、「(」と「)」それぞれに対して他の字句とは異なる戻り値を返す、というような内容を記述すればよいです。
∴・「(」と「)」に対してほかの字句とはそれぞれ別の戻り値を返す
・( と ) の字句に対しそれぞれ ( と ) を返す
広告
広告