平成27年春期試験問題 午前問6
問6解説へ
モンテカルロ法によって,正方形に内接する円の面積を近似的に求める方法はどれか。
- 円に内接する正多角形の面積によって求める。
- 正方形内に多数の小円を重ならないようにぎっしり詰めて,円の中にある小円の個数によって求める。
- 正方形内に乱数を用いて多数の点を一様に打ち,円の中にある点の個数によって求める。
- 正方形内を微細な間隔の格子点で区切り,円の中にある格子点の個数によって求める。
広告
解説
モンテカルロ法は、数値解析の分野において、確率を近似的に求めるために使われる手法です。乱数によるn回のシミュレーションを行い、ある事象がm回起これば、その事象の起こる確率は m/nで近似できます。試行回数nが大きくなるほどよりよい近似値を得ることができます。
モンテカルロ法は一様乱数を用いることが特徴なので正解は「ウ」です。
モンテカルロ法の例としてよく用いられるのが円周率の近似値を求める方法で、正方形内に乱数を用いて多数の点を打ち、「内接円内にある点の数/点を打った数」を計算することで円の面積を近似的に求め、そこから円周率を導きます。
以下は、プログラムを組んで正方形内へのランダムな打点を10,000回繰り返した結果です。正方形の面積を1とすると内接円の面積は
0.5×0.5×π=0.25π=π/4≒0.785
ですから、10,000回試行に対して内接円の内部の点の数が7,844個という結果は、正方形と内接円の面積比を概ね正確に表していると言えます。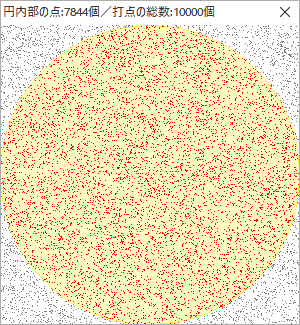
モンテカルロ法は一様乱数を用いることが特徴なので正解は「ウ」です。
モンテカルロ法の例としてよく用いられるのが円周率の近似値を求める方法で、正方形内に乱数を用いて多数の点を打ち、「内接円内にある点の数/点を打った数」を計算することで円の面積を近似的に求め、そこから円周率を導きます。
以下は、プログラムを組んで正方形内へのランダムな打点を10,000回繰り返した結果です。正方形の面積を1とすると内接円の面積は
0.5×0.5×π=0.25π=π/4≒0.785
ですから、10,000回試行に対して内接円の内部の点の数が7,844個という結果は、正方形と内接円の面積比を概ね正確に表していると言えます。

広告