平成29年春期試験午後問題 問3
問3 プログラミング
⇱問題PDF
探索アルゴリズムに関する次の記述を読んで,設問1~5に答えよ。
探索アルゴリズムに関する次の記述を読んで,設問1~5に答えよ。
広告
1個ずつの重さが異なる商品を組み合わせ,合計の重さが指定された値になるようにしたい。
この問題を次のように簡略化し,解法を考える。 例えば,指定されたn個の数が(10,34,55,77),目標Xが100とすると,選択した数の組合せは(10,34,55),選択した数の合計(以下,合計という)は99となる。
例えば,指定されたn個の数が(10,34,55,77),目標Xが100とすると,選択した数の組合せは(10,34,55),選択した数の合計(以下,合計という)は99となる。
この問題を解くためのアルゴリズムを考える。
指定されたn個の数の中から任意の個数を選択することから,各数に対して,選択する,選択しない,の二つのケースがある。数を一つずつ調べて,次の数がなくなるまで"選択する","選択しない"の分岐を繰り返すことで,任意の個数を選択する全ての組合せを網羅できる。この場合分けを図1に示す。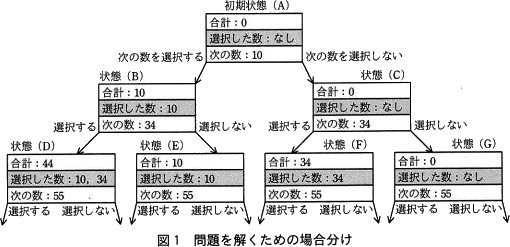 〔データ構造の検討〕
〔データ構造の検討〕
図1の場合分けをプログラムで実装するために,必要となるデータ構造を検討する。
まず,図1の場合分けを木構造とみなしたときの各ノード(状態)を構造体 Status で表す。構造体 Status は要素として"合計","選択した数',"次の数"をもつ必要がある。
プログラムで使用する配列,変数及び構造体を表1に示す。 〔探索の手順〕
〔探索の手順〕
図1に示した場合分けの初期状態(A)からの探索手順を,次の(1)~(3)に示す。①これから探索する状態を格納しておくためのデータ構造として,キューを使用する場合とスタックを使用する場合で,探索の順序が異なる。また,②データ構造によってメモリの使用量も異なる。ここではキューを使用することにする。
〔"取得した状態"の評価〕
"取得した状態"を評価し,"解答の候補"を設定する手順を,次の(1),(2)に示す。 〔探索処理関数 treeSearch〕
〔探索処理関数 treeSearch〕
探索処理を実装した関数 treeSearch のプログラムを図2に示す。
ここで,表1で定義した配列及び変数は,グローバル変数とする。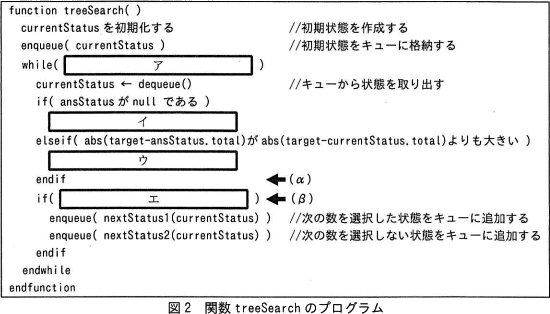 〔探索回数の削減〕
〔探索回数の削減〕
関数 treeSearch で実装した方法では,nが大きくなるにつれて"取得した状態"を評価する回数(以下,探索回数という)も増大するが,不要な探索処理を行わないようにすることによって,③探索回数を削減することができる。探索回数の削減のために,探索を継続するかどうかを示すフラグを新たに用意し,次の(1)~(3)の処理を追加することにした。 探索回数の削減を実装するために,図2中の(α)の行と(β)の行の間に図3のプログラムを追加し,β)を"if(エかつ,nextFlagが"Y"である)"に修正した。
探索回数の削減を実装するために,図2中の(α)の行と(β)の行の間に図3のプログラムを追加し,β)を"if(エかつ,nextFlagが"Y"である)"に修正した。
この問題を次のように簡略化し,解法を考える。

この問題を解くためのアルゴリズムを考える。
指定されたn個の数の中から任意の個数を選択することから,各数に対して,選択する,選択しない,の二つのケースがある。数を一つずつ調べて,次の数がなくなるまで"選択する","選択しない"の分岐を繰り返すことで,任意の個数を選択する全ての組合せを網羅できる。この場合分けを図1に示す。

図1の場合分けをプログラムで実装するために,必要となるデータ構造を検討する。
まず,図1の場合分けを木構造とみなしたときの各ノード(状態)を構造体 Status で表す。構造体 Status は要素として"合計","選択した数',"次の数"をもつ必要がある。
プログラムで使用する配列,変数及び構造体を表1に示す。

図1に示した場合分けの初期状態(A)からの探索手順を,次の(1)~(3)に示す。①これから探索する状態を格納しておくためのデータ構造として,キューを使用する場合とスタックを使用する場合で,探索の順序が異なる。また,②データ構造によってメモリの使用量も異なる。ここではキューを使用することにする。
- 初期状態(A)を作成し,キューに格納する。キューが空になるまで(2),(3)を繰り返す。
- キューに格納されている状態を一つ取り出す。これを"取得した状態"と呼ぶ。"取得した状態"の評価を行う(状態を評価する手順は次の〔"取得した状態"の評価〕に示す)。
- "取得した状態"に次の数がある場合,次の数を選択した状態と,次の数を選択しない状態をそれぞれ作成し,順にキューに格納する。
〔"取得した状態"の評価〕
"取得した状態"を評価し,"解答の候補"を設定する手順を,次の(1),(2)に示す。
- "解答の候補"がnullの場合,"取得した状態"を"解答の候補"にする。
- "解答の候補"nullでない場合,"解答の候補"の合計と"取得した状態"の合計をそれぞれ目標Xと比較して,後者の方が目標Xに近い場合,"取得した状態"を"解答の候補"にする。

探索処理を実装した関数 treeSearch のプログラムを図2に示す。
ここで,表1で定義した配列及び変数は,グローバル変数とする。

関数 treeSearch で実装した方法では,nが大きくなるにつれて"取得した状態"を評価する回数(以下,探索回数という)も増大するが,不要な探索処理を行わないようにすることによって,③探索回数を削減することができる。探索回数の削減のために,探索を継続するかどうかを示すフラグを新たに用意し,次の(1)~(3)の処理を追加することにした。
- "取得した状態"の合計が目標X以上の場合,以降の状態で数を選択しても合計は目標Xから離れてしまい,"解答の候補"にはならない。以降の状態の探索を不要とするために,フラグを探索中止に設定する。
- (1)以外の場合,フラグを探索継続に設定する。
- フラグが探索中止の場合,"取得した状態"からの分岐を探索しないようにする。探索回数の削減のために追加する変数を表3に示す。


広告
設問1
図2中のア~エに入れる適切な字句を答えよ。
解答例・解答の要点
ア:isEmpty()が0である
イ:ansStatus ← currentStatus
ウ:ansStatus ← currentStatus
エ:currentStatus.nextIndexが0ではない
イ:ansStatus ← currentStatus
ウ:ansStatus ← currentStatus
エ:currentStatus.nextIndexが0ではない
解説
〔アについて〕while文の()の中には継続条件式が入るので、繰返し処理に関する記述を本文中から探すと、本文中の〔探索の手順〕(1)で、「キューが空になるまで(2),(3)を繰り返す」とあります。プログラム中の繰返し文が4行目から始まる while文 1つしかないことから、プログラム中の5行目から14行目の処理が、(2)(3)の説明に相当する繰返し処理であるとわかります。よって、アには「キューが空でない」場合にループを繰り返す条件式が入ります。
そして、問題文の表2の関数群には、この用途にピッタリの isEmpty() が定義されています。
- isEmpty()
- キューが空かどうかを判定する。
キューが空ならば1を、そうでなければ0を返す。
∴ア=isEmpty()が0である
〔イについて〕
問題文の図2の6行目に、「if( ansStatusがnullである )」とあります。このことから、イには ansStatus(解答の候補) が null の場合に行う処理が入ることがわかります。問題文を読むと〔"取得した状態"の評価〕の(1)に、「"解答の候補"がnullの場合は、"取得した状態"を"解答の候補"にする」とあります。表1の currentStatus の説明にもあるように、その時点での"取得した状態"を格納する変数は currentStatus ですので、currentStatus(取得した状態) を ansStatus(解答の候補) に代入する処理を行うことになります。
したがって、イには「ansStatus ← currentStatus」が入ります。
なお、実際に「ansStatus ← currentStatus」の処理が行われるのは、ansStatus が初期値のnullになっている、whileループの1回目の処理のときのみです。
∴イ=ansStatus ← currentStatus
〔イについて〕
イと同様に、本文中の〔"取得した状態"の評価〕の説明を基に考えます。
問題文の図2の8行目に、「elseif( abs(target-ansStatus.total)がabs(target-currentStatus.total)よりも大きい )」とあります。条件式を要素に分解すると
- abs(target-ansStatus.total)
- 目標値(target)と、"解答の候補"の合計値の差の絶対値
- abs(target-currentStatus.total)
- 目標値(target)と、"取得した状態"の合計値の差の絶対値
ウの処理は、1つ前の行の条件式が真のときに実行される部分なので、"解答の候補"を"取得した状態"で更新する処理、すなわち「ansStatus ← currentStatus」が入ります。
∴ウ=ansStatus ← currentStatus
〔エについて〕
エでは、問題文の図2の12行目・13行目の処理を行う条件式が入ります。この2行の処理は、〔探索の手順〕の(3)より、「"取得した状態"に次の数がある場合,次の数を選択した状態と,次の数を選択しない状態をそれぞれ作成し,順にキューに格納する」に相当することがわかります。よって、エには「"取得した状態"に次の数がある」という意味の条件式が入ります。
表1の Status の説明より、次の数がない場合 nextIndex が 0 になっていることがわかるので、エには「"取得した状態"に次の数がある」場合に真となる条件式として「currentStatus.nextIndexが0ではない」が入ることになります。また「currentStatus.nextIndexが1以上」でも大丈夫でしょう。
∴エ=currentStatus.nextIndexが0ではない
広告
設問2
図3中のオ~カに入れる適切な字句を答えよ。
解答例・解答の要点
オ:"N"
カ:"Y"
カ:"Y"
解説
図3の追加プログラムを見ると「if( currentStatus.totalがtarget以上である )」という条件式で分岐しています。これは、〔探索回数の削減〕(1)(2)に相当する分岐処理になります。currentStatus.total は"取得した状態"の合計値、target は目標Xですから、"取得した状態"の合計値が、目標X以上の場合はオの行の処理が、そうでない(目標X未満の)場合にはカの行の処理が行われることになります。〔オについて〕
〔探索回数の削減〕(1)には、「"取得した状態"の合計が目標X以上の場合、…以降の探索を不要とするために,フラグを探索中止に設定する」とあります。探索回数の削減のために追加された変数である nextFlag は、"Y"のとき探索継続,"N"のとき探索中止を表すので、オには探索中止を表す"N"が入ります。
∴オ="N"
〔カについて〕
〔探索回数の削減〕(2)には、「(1)以外の場合,フラグを探索継続に設定する」とあるので、オとは逆に探索継続を表す"Y"を nextFlag に設定しなければなりません。よってカには"Y"が入ります。
∴カ="Y"
広告
設問3
本文中の下線①について,次の(1),(2)の場合の評価の順序を,図1中の状態の記号(A)~(G)を用いてそれぞれ答えよ。ここで,分岐の際は左側のノードから先にデータ構造に格納することとする。本問では(D),(E),(F),(G)の後の状態は考慮しなくてよい。
- [探索の手順〕での記述どおり,データ構造にキューを使用した場合
- 本文中のキューを全てスタックに置き換えた場合
解答例・解答の要点
- (A)→(B)→(C)→(D)→(E)→(F)→(G)
- (A)→(C)→(G)→(F)→(B)→(E)→(D)
解説
- キューは先入れ先出しのデータ構造です。プログラムの12行目・13行目より、先に次の数を選択した状態をキューに追加し、その後に次の数を選択しない場合の状態をキューに追加していることがわかります。具体的には、以下の手順でキューへの追加・取り出しが行われます([ ]はキューの内部です)。
- 初期状態Aをキューに追加する [A]
- 初期状態Aをキューから取り出す []→A
- 状態Bをキューに追加する [B]
- 状態Cをキューに追加する [C,B]
- 状態Bをキューから取り出す [C]→B
- 状態Dをキューに追加する [D,C]
- 状態Eをキューに追加する [E,D,C]
- 状態Cをキューから取り出す [E,D]→C
- 状態Fをキューに追加する [F,E,D]
- 状態Gをキューに追加する [G,F,E,D]
- 状態Dをキューから取り出す [G,F,E]→D
- 状態Eをキューから取り出す [G,F]→E
- 状態Fをキューから取り出す [G]→F
- 状態Gをキューから取り出す []→G
∴(A)→(B)→(C)→(D)→(E)→(F)→(G) - スタックは後入れ先出しのデータ構造です。(1)の処理をスタックに置き換えて考えると、スタックを使用した場合には、以下の手順で追加・取り出しが行われます([ ]はスタックの内部です)。
- 初期状態Aをスタックに追加する [A]
- 初期状態Aをスタックから取り出す []→A
- 状態Bをスタックに追加する [B]
- 状態Cをスタックに追加する [B,C]
- 状態Cをスタックから取り出す [B]→C
- 状態Fをスタックに追加する [B,F]
- 状態Gをスタックに追加する [B,F,G]
- 状態Gをスタックから取り出す [B,F]→G
- 状態Fをスタックから取り出す [B]→F
- 状態Bをスタックから取り出す []→B
- 状態Dをスタックに追加する [D]
- 状態Eをスタックに追加する [D,E]
- 状態Eをスタックから取り出す [D]→E
- 状態Dをスタックから取り出す []→D
∴(A)→(C)→(G)→(F)→(B)→(E)→(D)
広告
設問4
本文中の下線②について,データ構造にキューを使用した場合に,キューが必要とするメモリ使用量の最大値として適切な字句を解答群の中から選び,記号で答えよ。ここで,問題における数の個数をn,キューに状態を一つ格納するために必要なメモリ使用量をmとする。
解答群
- 2nm
- 2nm
- nm
- n2m
- (n+1)m
解答例・解答の要点
ア
解説
指定されたn個が(10, 34, 55, 77)の場合を考えます。4つの数それぞれに"選択する"と"選択しない"の2つのケースがあるため、全ての組合せを網羅すると「2×2×2×2=16=24個」の状態が存在します。これを一般化すると、指定された数がn個の場合には2n個の状態を用意しなければならないということがわかります。状態を1つ格納するのに必要なメモリ使用量が m ですから、指定された数がn個の場合に必要なメモリ領域は、状態数にメモリ使用量を乗じた「2nm」になります。
∴ア:2nm
広告
設問5
本文中の下線③における探索回数の削減を更に効率的に行うために,"指定されたn個の数"に実施しておくことが有効な事前処理の内容を20字以内で,その理由を25字以内でそれぞれ述べよ。
解答例・解答の要点
内容:数を降順にソートしておく (12文字)
理由:早い段階で探索を打ち切ることができる (18文字)
理由:早い段階で探索を打ち切ることができる (18文字)
解説
探索アルゴリズムでは事前にソートをしておくと、効率良く探索ができます。今回の問題では、"指定されたn個の数"を降順にソートしておくと、早い段階(木構造の根に近い部分で)で目標Xを超えるか否かを判断できるので、探索回数の削減に繋がります。これらのことから、内容は「数を降順にソートしておく」、理由は「早い段階で探索を打ち切ることができる」が適切です。
∴内容:数を降順にソートしておく
理由:早い段階で探索を打ち切ることができる
広告

広告