離散数学(全64問中19問目)
No.19解説へ
集合A，B，Cに対してA∪B∪Cが空集合であるとき，包含関係として適切なものはどれか。ここで，∪は和集合を，∩は積集合を，XはXの補集合を，また，X⊆YはXがYの部分集合であることを表す。
出典：平成27年秋期 問 2
- (A∩B) ⊆ C
- (A∩B) ⊆ C
- (A∩B) ⊆ C
- (A∩B) ⊆ C
広告
解説
部分集合とは、ある集合Xの全ての要素が他の集合Yに含まれる(内包される)という2つの集合同士の関係を表し、数学記号"⊆"を用いて「X ⊆ Y」と表記します。
まず設問の「A∪B∪Cが空集合」という記述から、すべての要素は集合A，B，Cのいずれかに含まれるという条件が付されていることが確認できます。さらに選択肢の右辺が全て「C」であるので、左辺の集合が集合Cに内包されているものをベン図に描いて導きます。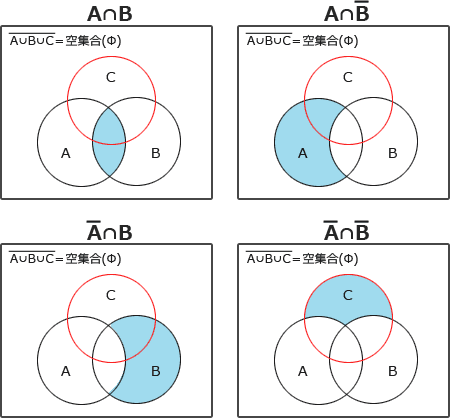
ベン図で表すとCの部分集合となるのは「A∩B」とわかります。
まず設問の「A∪B∪Cが空集合」という記述から、すべての要素は集合A，B，Cのいずれかに含まれるという条件が付されていることが確認できます。さらに選択肢の右辺が全て「C」であるので、左辺の集合が集合Cに内包されているものをベン図に描いて導きます。
広告