応用数学(全55問中28問目)
No.28解説へ
食品A及び食品Bの各1gに含まれる三つの成分1~3を調べたところ,含有量は表のようになった。成分1を70mg以上,成分2を80mg以上摂取するとき,成分3の最小摂取量は何mgか。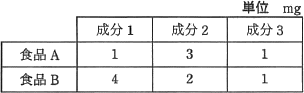

出典:平成24年秋期 問 2
- 28
- 31
- 32
- 34
広告
解説
線形計画法に則って考えると成分1を70mg以上,成分2を80mg以上摂取するには、以下の3通りの方法あります。
[1.食品Aのみで摂取]
食品Aのみで摂取する場合は、成分1の摂取量(70mg)を満たすために最低でも食品Aが70g必要となります。食品Aには1g当たり1mgの成分3が含まれているので、食品Aのみの場合の成分3の最小摂取量は「70mg」になります。
[2.食品Bのみで摂取]
食品Bのみで摂取する場合は、成分2の摂取量(80mg)を満たすために最低でも食品Bが40g必要となります。食品Bにも1g当たり1mgの成分3が含まれているので、成分3の最小摂取量は「40mg」になります。
[3.食品Aと食品Bを組合わせて摂取]
「成分1を70mg以上,成分2を80mg以上摂取可能」かつ「食品Aと食品Bの合計が最も少ない」という条件を満たす食品A,Bの摂取量を連立方程式を用いて導きます。
食品Aの摂取量をx,食品Bの摂取量をyとして、ちょうど成分1が70mg,成分2が80mgとなるxとyを式にすると、
{x+4y=70 …①(成分1)
{3x+2y=80 …②(成分2)
という式ができます。
後は普通に連立方程式を解いていくだけです。今回は代入法を使って解いていきます。
x+4y=70
x=70-4y …③
②の式中のxに③の式を代入
3(70-4y)+2y=80
210-12y+2y=80
-10y=-130
y=13 …④
①の式中のyに④を代入
x+4×13=70
x+52=70
x=18
以上の計算より、食品A,Bを組合わせた場合は、食品A 18g、食品B 13gで成分1,2の必要量を摂取可能とわかります。両方の食品とも1g当たり1mgの成分3が含まれているので、このパターンにおける成分3の最小摂取量は18mg+13mgで「31mg」です。
したがって3パターンのうちで最も少ない31mgが成分3の最小摂取量になります。よって「イ」が正解です。
- 食品Aのみで摂取
- 食品Bのみで摂取
- 食品Aと食品Bを組合わせて摂取
[1.食品Aのみで摂取]
食品Aのみで摂取する場合は、成分1の摂取量(70mg)を満たすために最低でも食品Aが70g必要となります。食品Aには1g当たり1mgの成分3が含まれているので、食品Aのみの場合の成分3の最小摂取量は「70mg」になります。
[2.食品Bのみで摂取]
食品Bのみで摂取する場合は、成分2の摂取量(80mg)を満たすために最低でも食品Bが40g必要となります。食品Bにも1g当たり1mgの成分3が含まれているので、成分3の最小摂取量は「40mg」になります。
[3.食品Aと食品Bを組合わせて摂取]
「成分1を70mg以上,成分2を80mg以上摂取可能」かつ「食品Aと食品Bの合計が最も少ない」という条件を満たす食品A,Bの摂取量を連立方程式を用いて導きます。
食品Aの摂取量をx,食品Bの摂取量をyとして、ちょうど成分1が70mg,成分2が80mgとなるxとyを式にすると、
{x+4y=70 …①(成分1)
{3x+2y=80 …②(成分2)
という式ができます。
後は普通に連立方程式を解いていくだけです。今回は代入法を使って解いていきます。
x+4y=70
x=70-4y …③
②の式中のxに③の式を代入
3(70-4y)+2y=80
210-12y+2y=80
-10y=-130
y=13 …④
①の式中のyに④を代入
x+4×13=70
x+52=70
x=18
以上の計算より、食品A,Bを組合わせた場合は、食品A 18g、食品B 13gで成分1,2の必要量を摂取可能とわかります。両方の食品とも1g当たり1mgの成分3が含まれているので、このパターンにおける成分3の最小摂取量は18mg+13mgで「31mg」です。
したがって3パターンのうちで最も少ない31mgが成分3の最小摂取量になります。よって「イ」が正解です。
広告