離散数学(全64問中44問目)
No.44解説へ
100人の学生を調べたところ,スペイン語を学んでいる者は18人,ドイツ語は40人,フランス語は42人であった。これら学生の中で,2言語以上を学んでいる者を調べると,スペイン語とドイツ語は6人,ドイツ語とフランス語は15人,フランス語とスペイン語は5人であり,その中には,3言語すべてを学んでいる者も2人いた。
いずれの言語も学んでいない学生は何人か。
いずれの言語も学んでいない学生は何人か。
出典:平成20年春期 問 6
- 22
- 24
- 26
- 28
広告
解説
全部を学んでいる人は、各2言語学んでいる人数にも重複して含まれているので、2言語学んでいる人数は問題文から全部学んでいる2人分を引いておく必要があります。
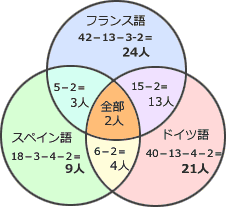 1つの言語のみを学んでいる人数は、
1つの言語のみを学んでいる人数は、
24+9+21=54(人)
2つの言語のみを学んでいる人数は、
3+4+13=20(人)
そして3言語すべてを学んでいる人数は2人です。
これらすべての領域の人数を足すと76人なので、いずれの言語も学んでいない学生は、
100-76=24(人)
したがって「イ」が正解です。
- [スペイン語とドイツ語のみ] 6人-2人=4人
- [ドイツ語とフランス語のみ] 15人-2人=13人
- [フランス語とスペイン語のみ] 5人-2人=3人

24+9+21=54(人)
2つの言語のみを学んでいる人数は、
3+4+13=20(人)
そして3言語すべてを学んでいる人数は2人です。
これらすべての領域の人数を足すと76人なので、いずれの言語も学んでいない学生は、
100-76=24(人)
したがって「イ」が正解です。
広告