離散数学(全64問中47問目)
No.47解説へ
全体集合S内に部分集合AとBがあるとき，A∩Bに等しいものはどれか。ここで，A∪BはAとBの和集合，A∩BはAとBの積集合，AはAの補集合，A－BはAからBを除いた差集合を表す。
出典：平成19年秋期 問 5
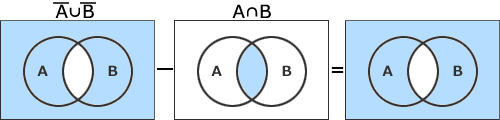
- (A∪B)－(A∩B)
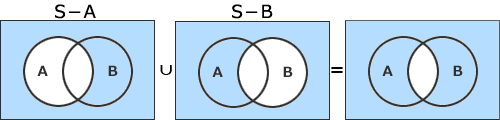
- (S－A)∪(S－B)
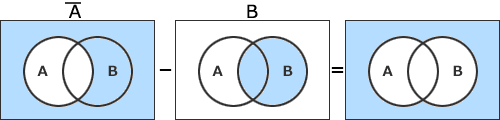
- A－B
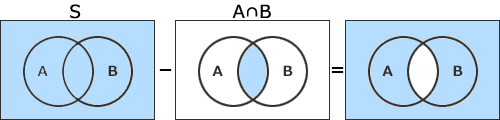
- S－(A∩B)
広告
解説
まずA∩Bをベン図で表してみると、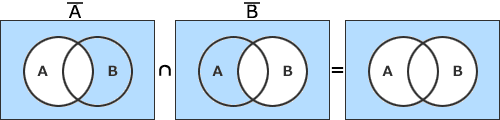
青の塗りつぶしが問題文の集合式が表す部分です。
同様に選択肢の論理式についてもベン図を使って解いていきます。最初から全部を表そうとするとややこしくなってしまうので、左辺と右辺を別々に考えてから最後にその二つをつなぎ合わせる方法を使うと、時間はかかりますが確実に解くことができると思います。
同様に選択肢の論理式についてもベン図を使って解いていきます。最初から全部を表そうとするとややこしくなってしまうので、左辺と右辺を別々に考えてから最後にその二つをつなぎ合わせる方法を使うと、時間はかかりますが確実に解くことができると思います。
広告