プロジェクトの時間(全60問中59問目)
No.59解説へ
アローダイアグラムで表される作業A~Hを見直したところ,作業Dだけが短縮可能であり,その所要日数を6日間に短縮できることが分かった。作業全体の所要日数は何日間短縮できるか。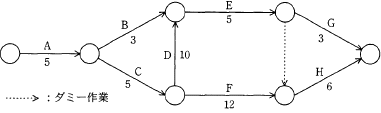

出典:平成18年春期 問47
- 1
- 2
- 3
- 4
広告
解説
アローダイアグラムの定番問題です。
まず、作業D短縮前の図におけるクリティカルパスを求めます。※ダミー作業は作業日数0日の作業として計算します。
次に、作業Dの作業日数が10日間から6日間に短縮された場合ですが、作業Dを含む2つのパスについて所要日数が以下のように変化します。
短縮前後の最短所要日数の差は「31日-28日=3日」ですので、作業全体の短縮日数は「3日」となります。
まず、作業D短縮前の図におけるクリティカルパスを求めます。※ダミー作業は作業日数0日の作業として計算します。
- A→B→E→G
- 5+3+5+3=16日
- A→B→E→(ダミー)→H
- 5+3+5+0+6=19日
- A→C→D→E→G
- 5+5+10+5+3=28日
- A→C→D→E→(ダミー)→H
- 5+5+10+5+0+6=31日
- A→C→F→H
- 5+5+12+6=28日
次に、作業Dの作業日数が10日間から6日間に短縮された場合ですが、作業Dを含む2つのパスについて所要日数が以下のように変化します。
- A→C→D→E→G
- 5+5+6+5+3=24日
- A→C→D→E→(ダミー)→H
- 5+5+6+5+0+6=27日
短縮前後の最短所要日数の差は「31日-28日=3日」ですので、作業全体の短縮日数は「3日」となります。
広告