アルゴリズム(全101問中44問目)
No.44解説へ
関数gcd(m,n)が次のように定義されている。m=135,n=35のとき,gcd(m,n) は何回呼ばれるか。ここで,最初の gcd(135,35) の呼出しも,1回に数えるものとする。また,m,n(m>n≧0)は整数とし,m mod n はmをnで割った余りを返すものとする。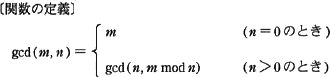
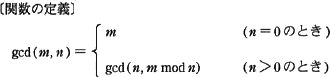
出典:平成24年春期 問 8
- 2
- 3
- 4
- 5
広告
解説
この再帰関数は拡張されたユークリッドの互除法を用いて整数m、nの最大公約数(Greatest Common Divisor:gcd)を求めるものです。
gcd(135, 35)を呼び出し、結果が返されるまでの流れは以下のようになります。
gcd(135, 35)を呼び出し、結果が返されるまでの流れは以下のようになります。
- gcd(135, 35)
n>0 なので、gcd(35, 135 mod 35) = gcd(35, 30) を呼び出す - gcd(35, 30)
n>0 なので、gcd(30, 35 mod 30) = gcd(30, 5) を呼び出す - gcd(30, 5)
n>0 なので、gcd(5, 30 mod 5) = gcd(5, 0) を呼び出す - gcd(5, 0)
n=0 なので、mの値である5を返す
広告