アルゴリズム(全101問中75問目)
No.75解説へ
次の流れ図は,シフト演算と加算の繰り返しによって2進数の乗算を行う手段を表したものである。この流れ図の中のa,bの処理の組合せとして,正しいものはどれか。ここで,乗数と被乗数は符号なしの16ビットで表される。X,Y,Zは32ビットのレジスタであり,けた送りには論理シフトを用いる。最下位ビットを第0ビットを記す。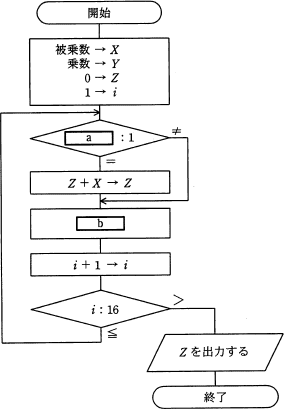

出典:平成19年秋期 問15
広告
解説
流れ図を見ると、被乗数がX、乗数がY、結果としてZを出力するので「X × Y = Z」が成立すれば良いことがわかります。
細かな説明がない流れ図の穴埋めでは論理的に答えを導くのは難しいので、XおよびYにトレースが簡単な数値を設定して、出力Zが適切な値かどうかで正しい組合せを探すのが確実な解法です。ここではX=3,Y=3を使います(16ビット表記だと「0000 0000 0000 0011)。また、あるビット列を左に1ビットシフトすると2倍、右に1ビットシフトすると1/2したのと同じになります(ビットあふれは無視します)。
このアルゴリズムを一言で言うならば、Yの第nビットが1であれば、ZにX×2nを加算する処理を繰り返すものということになります。
おまけとしてこのアルゴリズムをJavaScriptで実装したソースプログラムを掲載します。実行環境で数値やシフト部分を変えてお試しください。
細かな説明がない流れ図の穴埋めでは論理的に答えを導くのは難しいので、XおよびYにトレースが簡単な数値を設定して、出力Zが適切な値かどうかで正しい組合せを探すのが確実な解法です。ここではX=3,Y=3を使います(16ビット表記だと「0000 0000 0000 0011)。また、あるビット列を左に1ビットシフトすると2倍、右に1ビットシフトすると1/2したのと同じになります(ビットあふれは無視します)。
- Yの0ビット目は1なので、Z←(0+3) //Z=3
- Xを1ビット左シフト //X=6
- Yを1ビット右シフト //Y=1
- i←(1+1) //i=2
- Yの第0ビットは1なので、Z←(3+6) //Z=9
- Xを1ビット左シフト //X=12
- Yを1ビット右シフト //Y=0
- 以後、Yの第0ビットはi>16になるまで0なので、加算は行われずにループ終了
- Zを出力する //Z=9
- Yの第0ビットは1なので、Z←(0+3) //Z=3
- Xを1ビット右シフト //X=1
- Yを1ビット左シフト //Y=6
- i←(1+1) //i=2
- Yを左にシフトすると第0ビットに0が挿入される。以後、Yの第0ビットはi>16になるまで常に0なので、加算は行われずにループ終了
- Zを出力する //Z=3
- Yの第15ビットは0なので加算はなし
- Xを1ビット左シフト //X=6
- Yを1ビット右シフト //Y=1
- i←(1+1) //i=2
- Yを右にシフトすると第15ビットには0が挿入される。以後、Yの第15ビットはi>16になるまで常に0なので、加算は行われずにループ終了
- Zを出力する //Z=0
- Yの第15ビットは0なので加算はなし
- Xを1ビット右シフト //X=1
- Yを1ビット左シフト //Y=6
- i←(1+1) //i=2
- Yの第15ビットは0なので加算はなし
- Xを1ビット右シフト //X=0
- Yを1ビット左シフト //Y=12
- Xが0になったので、加算処理が行われたとしてもZは0のままでループ終了
- Zを出力する //Z=0
このアルゴリズムを一言で言うならば、Yの第nビットが1であれば、ZにX×2nを加算する処理を繰り返すものということになります。
おまけとしてこのアルゴリズムをJavaScriptで実装したソースプログラムを掲載します。実行環境で数値やシフト部分を変えてお試しください。
広告