令和3年秋期試験午後問題 問3
問3 プログラミング
⇱問題PDF
一筆書きに関する次の記述を読んで，設問1～4に答えよ。
一筆書きに関する次の記述を読んで，設問1～4に答えよ。
広告
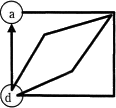
グラフは，有限個の点の集合と，その中の2点を結ぶ辺の集合から成る数理モデルである。グラフの点と点の間をつなぐ辺の列のことを経路という。本問では，任意の2点間で，辺をたどることで互いに行き来することができる経路が存在する(以下，強連結という)有向グラフを扱う。強連結な有向グラフの例を図1に示す。辺は始点と終点の組で定義する。各辺には1から始まる番号が付けられている。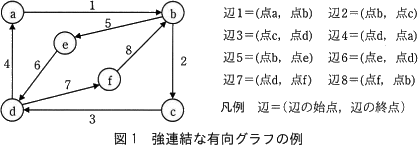
〔一筆書き〕
本問では，グラフの全ての辺を1回だけ通り，出発点から出て出発点に戻る閉じた経路をもつグラフを，一筆書きができるグラフとする。
〔一筆書きの経路の求め方〕
一筆書きの経路を求めるためには，出発点から辺の向きに従って辺を順番にたどり，出発点に戻る経路を見つける探索を行う。たどった経路(以下，探索済の経路という)について，グラフ全体で通過していない辺(以下，未探索の辺という)がない場合は，この経路が一筆書きの経路となる。未探索の辺が残っている場合は，探索済の経路を，未探索の辺が接続する点まで遡り，その点を出発点として，同じ点に戻る経路を見つけて，遡る前までの経路に連結することを繰り返す。
各点を始点とする辺を接続辺という。グラフの各点に対して接続辺の集合が決まり，辺の番号が一番小さい接続辺を最初の接続辺という。同じ始点をもつ接続辺の集合で，辺の番号を小さいものから順番に並べたときに，辺の番号が次に大きい接続辺を次の接続辺ということにする。
図1のグラフの各点の接続辺の集合を表1に示す。図1において，点bの最初の接続辺は辺2である。辺2の次の接続辺は辺5となる。辺5の次の接続辺はない。
一筆書きの経路の探索において，一つの点に複数の接続辺がある場合には，最初の接続辺から順にたどることにする。
図1のグラフで点aを出発点とした一筆書きの経路の求め方を図2に示す。
経路を構成する辺とその順番が，これ以上変わらない場合，確定済の経路という。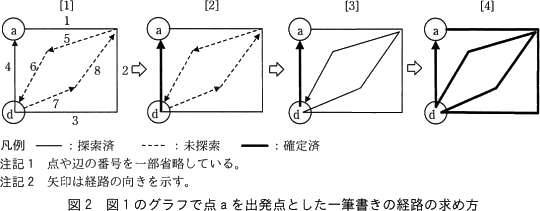
図2を参考にした一筆書きの経路を求める手順を次に示す。
〔一筆書きの経路を求める手順〕
点aから探索する場合は，点aの最初の接続辺である辺1から始め，辺1の終点bの最初の接続辺である辺2をたどり，同様に辺3，辺4をたどる。辺4の終点aからたどれる未探索の辺は存在しないので，これ以上探索が進められない(図2[1])。
しかし，未探索の辺5，辺6，辺7，辺8が残っているので，未探索の辺が接続する点まで遡る。
終点aから辺4を遡ると，辺4の始点dで未探索の辺7が接続している。遡った経路は途中で未探索の辺が存在しないので，これ以上，辺の順番が変わらず，辺4は，一筆書きの経路の一部として確定済の経路となる(図2[2])。
点dから同様に辺7→辺8→辺5→辺6と探索できるので，辺3までの経路と連結した新しい探索済の経路ができる(図2[3])。
辺6の終点dからは，辺6→辺5→辺8→辺7→辺3→辺2→辺1と出発点の点aまで遡り，これ以上，未探索の辺がないことが分かるので，全ての辺が確定済の経路になる(図2[4])。
一筆書きの経路は，次の(1)～(4)の手順で求められる。
一筆書きの経路を求める関数 directedE のプログラムを作成した。
実装に当たって，各点を点n(nは1～N)と記す。例えば，図1のグラフでは，点aは点1，点bは点2と記す。
グラフの探索のために，あらかじめ，グラフの点に対する最初の接続辺の配列 edgefirst 及び接続辺に対する次の接続辺の配列 edgenext を用意しておく。edgenext において，次の接続辺がない場合は，要素に0を格納する。
図1のグラフの場合の配列 edgefirst，edgenext を図3に示す。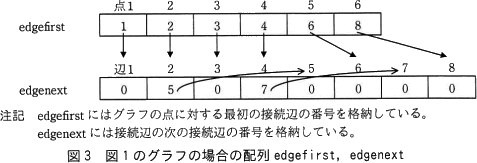
edgefirst によって点2の最初の接続辺が辺2であることが分かり，点2から最初にたどる接続辺は辺2となる。edgenext によって，辺2の次の接続辺が辺5であることが分かるので，点2から次にたどる接続辺は辺5となる。辺5の次の接続辺はないので，点2からたどる接続辺はこれ以上ないことが分かる。
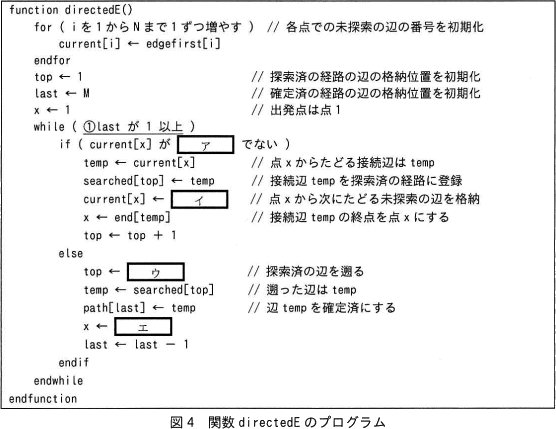
プログラム中で使用する定数と配列を表2に，作成した関数 directedE のプログラムを図4に示す。
全ての配列の添字は1から始まる。
本問では，グラフの全ての辺を1回だけ通り，出発点から出て出発点に戻る閉じた経路をもつグラフを，一筆書きができるグラフとする。
〔一筆書きの経路の求め方〕
一筆書きの経路を求めるためには，出発点から辺の向きに従って辺を順番にたどり，出発点に戻る経路を見つける探索を行う。たどった経路(以下，探索済の経路という)について，グラフ全体で通過していない辺(以下，未探索の辺という)がない場合は，この経路が一筆書きの経路となる。未探索の辺が残っている場合は，探索済の経路を，未探索の辺が接続する点まで遡り，その点を出発点として，同じ点に戻る経路を見つけて，遡る前までの経路に連結することを繰り返す。
各点を始点とする辺を接続辺という。グラフの各点に対して接続辺の集合が決まり，辺の番号が一番小さい接続辺を最初の接続辺という。同じ始点をもつ接続辺の集合で，辺の番号を小さいものから順番に並べたときに，辺の番号が次に大きい接続辺を次の接続辺ということにする。
図1のグラフの各点の接続辺の集合を表1に示す。図1において，点bの最初の接続辺は辺2である。辺2の次の接続辺は辺5となる。辺5の次の接続辺はない。
図1のグラフで点aを出発点とした一筆書きの経路の求め方を図2に示す。
経路を構成する辺とその順番が，これ以上変わらない場合，確定済の経路という。
〔一筆書きの経路を求める手順〕
点aから探索する場合は，点aの最初の接続辺である辺1から始め，辺1の終点bの最初の接続辺である辺2をたどり，同様に辺3，辺4をたどる。辺4の終点aからたどれる未探索の辺は存在しないので，これ以上探索が進められない(図2[1])。
しかし，未探索の辺5，辺6，辺7，辺8が残っているので，未探索の辺が接続する点まで遡る。
終点aから辺4を遡ると，辺4の始点dで未探索の辺7が接続している。遡った経路は途中で未探索の辺が存在しないので，これ以上，辺の順番が変わらず，辺4は，一筆書きの経路の一部として確定済の経路となる(図2[2])。
点dから同様に辺7→辺8→辺5→辺6と探索できるので，辺3までの経路と連結した新しい探索済の経路ができる(図2[3])。
辺6の終点dからは，辺6→辺5→辺8→辺7→辺3→辺2→辺1と出発点の点aまで遡り，これ以上，未探索の辺がないことが分かるので，全ての辺が確定済の経路になる(図2[4])。
一筆書きの経路は，次の(1)～(4)の手順で求められる。
- 一筆書きの経路の出発点を決める。
- 出発点から，未探索の辺が存在する限り，その辺をたどり，たどった経路を探索済の経路に追加する。
- 探索済の経路を未探索の辺が接続する点又は一筆書きの経路の出発点まで遡る。遡った経路は，探索済の経路から確定済の経路にする。未探索の辺が接続する点がある場合は，それを新たな出発点として，(2)に戻って新たな経路を見つける。
- 全ての辺が確定済の経路になった時点で探索が完了して，その確定済の経路が一筆書きの経路になる。
一筆書きの経路を求める関数 directedE のプログラムを作成した。
実装に当たって，各点を点n(nは1～N)と記す。例えば，図1のグラフでは，点aは点1，点bは点2と記す。
グラフの探索のために，あらかじめ，グラフの点に対する最初の接続辺の配列 edgefirst 及び接続辺に対する次の接続辺の配列 edgenext を用意しておく。edgenext において，次の接続辺がない場合は，要素に0を格納する。
図1のグラフの場合の配列 edgefirst，edgenext を図3に示す。
プログラム中で使用する定数と配列を表2に，作成した関数 directedE のプログラムを図4に示す。
全ての配列の添字は1から始まる。
広告
設問1
図4中のア～エに入れる適切な字句を答えよ。
解答例・解答の要点
ア：0
イ：edgenext[temp]
ウ：top－1
エ：start[temp]
イ：edgenext[temp]
ウ：top－1
エ：start[temp]
解説
解説の便宜上、プログラムに行番号を振っておきます。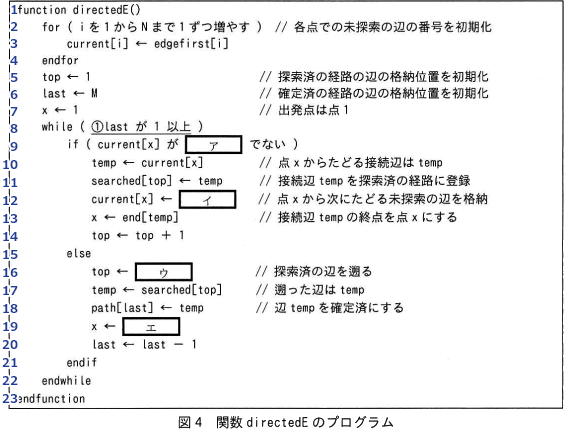
コメント部の記述より、if文が真のときには未探索の辺をたどる処理、偽のときには探索済の辺を遡る処理を行うとわかりますから、接続辺をたどる処理を行う条件を考えます。問題文を読むと、一筆書きの経路を求める手順(2)に「出発点から，未探索の辺が存在する限り，その辺をたどり，たどった経路を探索済の経路に追加する」と記載があるので、接続辺をたどるのは、その点について未探索の辺が存在する場合であることがわかります。
配列 current には、各点における次に探索すべき接続辺の番号（その点について未探索の接続辺がない場合には0）が格納されています。点xについて未探索の辺が存在するとき、current[x] は0以外になっていますから、これを分岐条件とすることができます。すなわち、"0以外"であればたどる処理、"0"であれば遡る処理というように分岐させることになります。したがって[ア]には「0」が当てはまります。
∴ア＝0
〔イについて〕
コメント部の記述より、12行目の処理は、点xにおける次にたどる未探索辺を更新する処理であることがわかります。[イ]は current[x] に代入する値であるため、次にたどる未探索辺の番号を示す式が入ります。図1の例で言うと、点bから辺2をたどったときに、点bにおける次にたどるべき接続辺を辺5に変えておく感じです。辺2に対する辺5のように、ある辺に対する次の接続辺は配列 edgenext に格納されています（表2の説明参照）。上記の例で次の接続辺である辺5を取得するためには、今たどった辺の番号"2"を使って edgenext[2] と指定することになります。プログラム中で今たどった辺の番号は変数 temp に格納されているため、辺 temp の次の接続辺の番号は edgenext[temp] で取得することができます。したがって[イ]には「edgenext[temp]」が当てはまります。
※current[x] は temp に代入後変更されていないので、代入元の値を使った edgenext[current[x]] でも正しく動作します。
∴イ＝edgenext[temp]
〔ウについて〕
代入先の変数 top は、変数定義部のコメントより「探索済の経路の辺の格納位置」を表すことがわかっています。探索済の経路の辺は配列 searched の要素1から順に格納されていますが、配列 searched 上の現在位置を示すのが変数 top の役割です。
変数 top の動きを見ていくと、11行目で配列 searched の格納位置として使われた後、14行目でインクリメント(+1)されています。つまり、変数 top は、配列 searched 上で次の接続辺を格納する位置を保持していることになります。この"次の"というのがポイントです。
17行目では temp ← searched[top] で遡った辺（直前にたどった辺）を取得していますが、変数 top は"次の"接続辺の格納位置ですから、直前にたどった辺を取得するには1つ前の要素を参照しなければなりません。そこで、17行目の処理前に変数 top をデクリメント(-1)する処理が必要となります。したがって[ウ]には「top－1」が当てはまります。
∴ウ＝top－1
〔エについて〕
変数 x は、配列 current の添字に使われている変数で、処理対象となる点の番号を保持します。辺を遡ったときには次に処理するのは1つ前の点になりますから、これを取得するための式が入ります。ある辺に対する始点の番号は配列 start に格納されていて、辺mの始点の番号は start[m] で取得可能です（表2の説明参照）。プログラム中で今遡った辺の番号は変数 temp に格納されていますから、辺 temp の始点の番号は start[temp] で取得することができます。したがって[エ]には「start[temp]」が当てはまります。
※start[path[last]] や start[searched[top]] でも正しく動作します。
∴エ＝start[temp]
広告
設問2
図1のグラフで関数 directedE を動作させたとき，while文中のif文は，何回実行されるか，数値で答えよ。
解答例・解答の要点
16
解説
while文の中では、"接続辺をたどる"または"接続辺を遡る"のどちらかを行います。すなわち、while文を繰り返す回数とは探索終了までに"接続辺をたどる回数"と"接続辺を遡る回数"の合計です。本プログラムでは、接続辺をたどった後にその接続辺を遡ることで経路の一部として確定し、一度たどった辺を再度たどることはないので、「接続辺をたどる回数＝接続辺を遡る回数＝辺の数」となります。図1の辺の数は8なので、while文を繰り返す回数は「8×2＝16回」となります。具体的に、図1の一筆書きの経路を求める流れは、以下のようになります。
- 点a→点b 辺1をたどる
- 点b→点c 辺2をたどる
- 点c→点d 辺3をたどる
- 点d→点a 辺4をたどる
- 点a→点d 辺4を遡る（path[8] = 4）
- 点d→点f 辺7をたどる
- 点f→点b 辺8をたどる
- 点b→点e 辺5をたどる
- 点e→点d 辺6をたどる
- 点d→点e 辺6を遡る（path[7] = 6）
- 点e→点b 辺5を遡る（path[6] = 5）
- 点b→点f 辺8を遡る（path[5] = 8）
- 点f→点d 辺7を遡る（path[4] = 7）
- 点d→点c 辺3を遡る（path[3] = 3）
- 点c→点b 辺2を遡る（path[2] = 2）
- 点b→点a 辺1を遡る（path[1] = 1）
∴16
広告
設問3
一筆書きができない強連結な有向グラフで関数 directedE を動作させたとき，探索はどのようになるかを，解答群の中から選び，記号で答えよ。
解答群
- 探索が完了するが，配列 path に格納された経路は一筆書きの経路にならない。
- 探索が完了せずに終了して，配列 path に格納された経路は一筆書きの経路にならない。
- 探索が無限ループに陥り，探索が終了しない。
解答例・解答の要点
ア
解説
一筆書きができない形状のときにどうなるかをトレースしてみるとわかりやすいと思います。例として、図1に1つの辺（辺9）を加えた以下のグラフで考えてみます。※配列 path は0で初期化されていると仮定しています。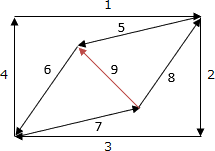
- 辺1、辺2、辺3、辺4の順にたどります。
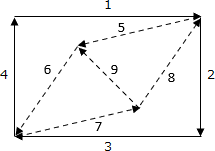
- 辺4を遡ります。
path = [0, 0, 0, 0, 0, 0, 0, 0, 4]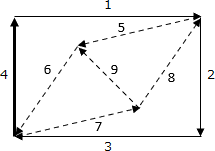
- 辺7、辺8、辺5、辺6の順にたどります。
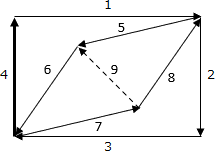
- 辺6、辺5、辺8の順に遡ります。
path = [0, 0, 0, 0, 0, 8, 5, 6, 4]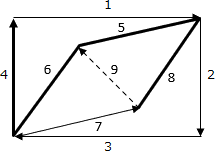
- 辺9をたどります。
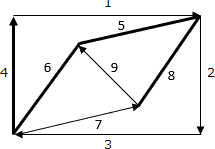
- 辺9、辺7、辺3、辺2、辺1の順に遡ります。
path = [1, 2, 3, 7, 9, 8, 5, 6, 4]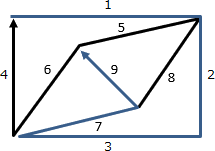
- path[1] まで埋まり last が0になるので探索終了
∴ア：探索が完了するが，配列 path に格納された経路は一筆書きの経路にならない。
広告
設問4
図4のプログラムは，配列 searched を配列 path に置き換えることで，使用する領域を減らすことができる。このとき，無駄な繰返しが発生しないように，下線①の繰返し条件を，変数 top と last を用いて変更せよ。
解答例・解答の要点
topがlast以下
解説
図1のグラフを例として、配列 searched を配列 path に置き換えると、1つの配列で探索済経路の記録と確定済経路の記録を行うことになります。繰返し条件として top とlast を使用することが明らかになっているので、設問2で求めた探索手順に沿って、top、last 及び path の変化を考えます。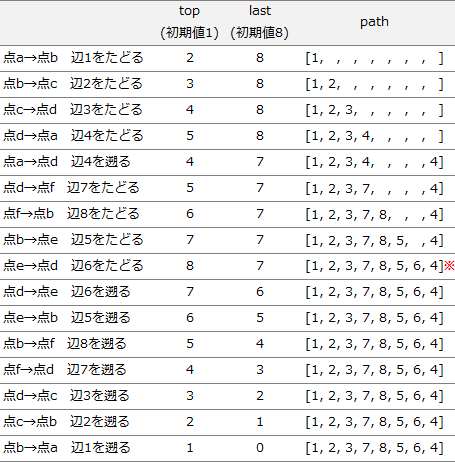
※lastがtop以上、last－topが0以上など、topがlastを超えない限り繰り返す条件であればすべて正解かと思います。
∴topがlast以下
広告
広告