令和4年秋期試験午後問題 問3
問3 プログラミング
⇱問題PDF
迷路の探索処理に関する次の記述を読んで,設問に答えよ。
迷路の探索処理に関する次の記述を読んで,設問に答えよ。
広告
始点と終点を任意の場所に設定するn×mの2次元のマスの並びから成る迷路の解を求める問題を考える。本問の迷路では次の条件で解を見つける。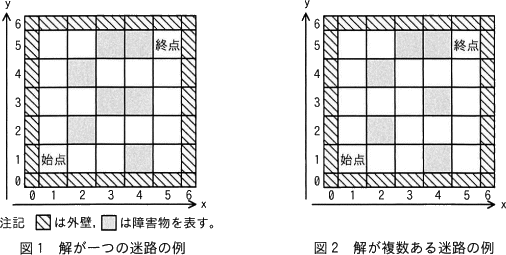 〔迷路の解を見つける探索〕
〔迷路の解を見つける探索〕
迷路の解を全て見つける探索の方法を次のように考える。
迷路と外壁の各マスの位置をx座標とy座標で表し,各マスについてそのマスに関する情報(以下,マス情報という)を考える。与えられた迷路に対して,障害物と外壁のマス情報にはNGフラグを,それ以外のマス情報にはOKフラグをそれぞれ設定する。マス情報全体を迷路図情報という。
探索する際の"移動"には,"進む"と"戻る"の二つの動作がある。"進む"は,現在いるマスから①y座標を1増やす,②x座標を1増やす,③y座標を1減らす,④x座標を1減らす,のいずれかの方向に動くことである。マスに"進む"と同時にそのマスのマス情報に足跡フラグを入れる。足跡フラグが入ったマスには"進む"ことはできない。"戻る"は,今いるマスから"進んで"きた一つ前のマスに動くことである。マスに"移動"したとき,移動先のマスを"訪問"したという。
探索は,始点のマスのマス情報に足跡フラグを入れ,始点のマスを"訪問"したマスとして,始点のマスから開始する。現在いるマスから次のマスに"進む"試みを①~④の順に行い,もし試みた方向のマスに"進む"ことができないならば,次の方向に"進む"ことを試みる。4方向いずれにも"進む"ことができないときには,現在いるマスのマス情報をOKフラグに戻し,一つ前のマスに"戻る"。これを終点に到達するまで繰り返す。終点に到達したとき,始点から終点まで"進む"ことでたどってきたマスの並びが迷路の解の一つとなる。
迷路の解を見つけた後も,他の解を見つけるために,終点から一つ前のマスに"戻り",迷路の探索を続け,全ての探索を行ったら終了する。迷路を探索している間それまでの経過をスタックに格納しておく。終点にたどり着いた時点でスタックの内容を順番にたどると,それが解の一つになる。
図1の迷路では,始点から始めて,(1,1)→(1,2)→(1,3)→(1,4)→(1,5)→(2,5)→(1,5)→(1,4)のように"移動"する。ここまででマスの"移動"は7回起きていて,このときスタックには経過を示す4個の座標が格納されている。さらに探索を続けて,始めから13回目の"移動"が終了した時点では,スタックにはア個の座標が格納されている。
〔迷路の解を全て求めて表示するプログラム〕
迷路の解を全て求めて表示するプログラムを考える。プログラム中で使用する主な変数,定数及び配列を表1に示す。配列の添字は全て0から始まり,要素の初期値は全て0とする。迷路を探索してマスを"移動"する関数 visit のプログラムを図3に,メインプログラムを図4に示す。メインプログラム中の変数及び配列は大域変数とする。 〔解が複数ある迷路〕
〔解が複数ある迷路〕
図2は解が複数ある迷路の例で,一つ目の解が見つかった後に,他の解を見つけるために,迷路の探索を続ける。一つ目の解が見つかった後で,最初に実行される関数 visit の引数の値は力である。この引数の座標を基点として二つ目の解が見つかるまでに,マスの"移動"はキ回起き,その間に座標が(4,2)のマスはク回"訪問"される。
- 迷路内には障害物のマスがあり,n×mのマスを囲む外壁のマスがある。障害物と外壁のマスを通ることはできない。
- 任意のマスから,そのマスに隣接し,通ることのできるマスに移動できる。迷路の解とは,この移動の繰返しで始点から終点にたどり着くまでのマスの並びである。ただし,迷路の解では同じマスを2回以上通ることはできない。
- 始点と終点は異なるマスに設定されている。

迷路の解を全て見つける探索の方法を次のように考える。
迷路と外壁の各マスの位置をx座標とy座標で表し,各マスについてそのマスに関する情報(以下,マス情報という)を考える。与えられた迷路に対して,障害物と外壁のマス情報にはNGフラグを,それ以外のマス情報にはOKフラグをそれぞれ設定する。マス情報全体を迷路図情報という。
探索する際の"移動"には,"進む"と"戻る"の二つの動作がある。"進む"は,現在いるマスから①y座標を1増やす,②x座標を1増やす,③y座標を1減らす,④x座標を1減らす,のいずれかの方向に動くことである。マスに"進む"と同時にそのマスのマス情報に足跡フラグを入れる。足跡フラグが入ったマスには"進む"ことはできない。"戻る"は,今いるマスから"進んで"きた一つ前のマスに動くことである。マスに"移動"したとき,移動先のマスを"訪問"したという。
探索は,始点のマスのマス情報に足跡フラグを入れ,始点のマスを"訪問"したマスとして,始点のマスから開始する。現在いるマスから次のマスに"進む"試みを①~④の順に行い,もし試みた方向のマスに"進む"ことができないならば,次の方向に"進む"ことを試みる。4方向いずれにも"進む"ことができないときには,現在いるマスのマス情報をOKフラグに戻し,一つ前のマスに"戻る"。これを終点に到達するまで繰り返す。終点に到達したとき,始点から終点まで"進む"ことでたどってきたマスの並びが迷路の解の一つとなる。
迷路の解を見つけた後も,他の解を見つけるために,終点から一つ前のマスに"戻り",迷路の探索を続け,全ての探索を行ったら終了する。迷路を探索している間それまでの経過をスタックに格納しておく。終点にたどり着いた時点でスタックの内容を順番にたどると,それが解の一つになる。
図1の迷路では,始点から始めて,(1,1)→(1,2)→(1,3)→(1,4)→(1,5)→(2,5)→(1,5)→(1,4)のように"移動"する。ここまででマスの"移動"は7回起きていて,このときスタックには経過を示す4個の座標が格納されている。さらに探索を続けて,始めから13回目の"移動"が終了した時点では,スタックにはア個の座標が格納されている。
〔迷路の解を全て求めて表示するプログラム〕
迷路の解を全て求めて表示するプログラムを考える。プログラム中で使用する主な変数,定数及び配列を表1に示す。配列の添字は全て0から始まり,要素の初期値は全て0とする。迷路を探索してマスを"移動"する関数 visit のプログラムを図3に,メインプログラムを図4に示す。メインプログラム中の変数及び配列は大域変数とする。

図2は解が複数ある迷路の例で,一つ目の解が見つかった後に,他の解を見つけるために,迷路の探索を続ける。一つ目の解が見つかった後で,最初に実行される関数 visit の引数の値は力である。この引数の座標を基点として二つ目の解が見つかるまでに,マスの"移動"はキ回起き,その間に座標が(4,2)のマスはク回"訪問"される。
広告
設問1
〔迷路の解を見つける探索〕について答えよ。
- 図1の例で終点に到達したときに,この探索で"訪問"されなかったマスの総数を,障害物と外壁のマスを除き答えよ。
- 本文中のアに入れる適切な数値を答えよ。
解答例・解答の要点
- 3
- ア:2
解説
問題文中で述べられている迷路の表現方法(迷路図情報)をまとめると、以下のようになります。- 各マスの位置をx座標とy座標で表し、各マスに対応するマス情報を設定して迷路を表現する
- 進入不可の障害物と外壁マスはNGフラグ、始点マスと訪問済のマスには足跡フラグ、まだ進んでいないマスにはOKフラグが設定される
- 始点のマスから、"進む"または"戻る"の2種類の"移動"によって探索を行う
- "進む"は、上(①y座標を1増やす)⇒右(②x座標を1増やす)⇒下(③y座標を1減らす)⇒左(④x座標を1減らす)の順で行う
- "進む"ことができない場合、そのマスをOKフラグに戻してから1つ前のマスに"戻る"
- 終点に到達するまで、"進む"または"戻る"を繰り返す
"移動"とは、"進む"と"戻る"の二つの動作です。"進む"動作は、上⇒右⇒下⇒左の順で行われることを踏まえて、初期状態から"移動"が13回発生するまでの流れを追跡すると以下のようになります。オレンジ色のマスは足跡フラグが設定されているマス、すなわちスタックに格納されている座標を表しています。
- 上に進めるので、始点(1,1)から上のマス(1,2)に進む
- 上に進めるので、(1,2)から上のマス(1,3)に進む
- 上に進めるので、(1,3)から上のマス(1,4)に進む
- 上に進めるので、(1,4)から上のマス(1,5)に進む
- 上に進めないので、(1,2)から右のマス(2,5)に進む
- 4方向のいずれもOKマスではないので、(2,5)から左のマス(1,5)に戻る
- 4方向のいずれもOKマスではないので、(1,5)から左のマス(1,4)に戻る
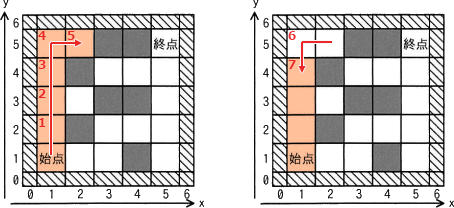
- 4方向のいずれもOKマスではないので、(1,4)から左のマス(1,3)に戻る
- 右に進めるので、(1,3)から上のマス(2,3)に進む
- 4方向のいずれもOKマスではないので、(2,3)から左のマス(1,3)に戻る
- 4方向のいずれもOKマスではないので、(1,3)から左のマス(1,2)に戻る
- 4方向のいずれもOKマスではないので、(1,2)から左のマス(1,1)に戻る
- 右に進めるので、(1,1)から上のマス(2,1)に進む
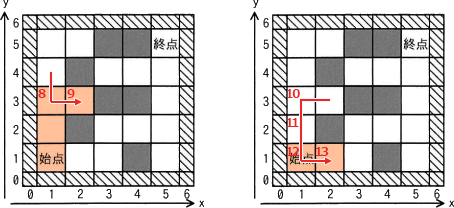
∴(1)=3
(2)=2
広告
設問2
図3中のイ~エに入れる適切な字句を答えよ。
解答例・解答の要点
イ:paths[sol_num] [k]
ウ:stack_top - 1
エ:maze[x] [y]
ウ:stack_top - 1
エ:maze[x] [y]
解説
解説の便宜上、プログラムに行番号を振っておきます。
4行目のif文の条件式より、5~8行目は訪問したマスが終点だったときの処理であることがわかります。問題文を読むと「終点にたどり着いた時点でスタックの内容を順番にたどると,それが解の一つになる」とあり、現在のスタックの内容で解の一つが確定することがわかります。メインプログラムのほうでは解を出力する処理として配列 paths の印字処理がありますが、関数 visit のほうには配列 paths に値を設定する処理がどこにも記述されていません。このままだとメインプログラムで出力される paths は常に空となってしまいますから、5~8行目で行うべきは配列 paths に解を格納する処理であると判断できます。
配列 paths[u][v] は2次元配列で、uは解の番号を示す添字、u番目の解を構成する各座標の順番を表すのがvです。
配列 paths に格納される解の例
paths[0] = [(1,1), (1,2), (1,3), (2,3), (3,3), (3,4), (4,4), (5,4), (5,5)]
paths[1] = [(1,1), (1,2), (1,3), (2,3), (3,3), (3,2), (4,2), (5,2), (5,3), (5,4), (5,5)]
最初に見つかった解は paths[0] に格納、2番目に見つかった解は paths[1] に格納という感じになります。プログラム中では解を見つけた総数を保持する変数として sol_num があります。変数 sol_num の初期値は0であり、8行目で解が見つかるごとに1ずつ増えていくようになっています。変数 sol_num を添字uに使えば、1つ目の解が見つかったときには paths[0]、2つ目の解が見つかったときには paths[1] が代入先となるので解を適切に格納することができます。paths[0] = [(1,1), (1,2), (1,3), (2,3), (3,3), (3,4), (4,4), (5,4), (5,5)]
paths[1] = [(1,1), (1,2), (1,3), (2,3), (3,3), (3,2), (4,2), (5,2), (5,3), (5,4), (5,5)]
次に添字vに使う式を考えます。5行目にあるfor文は配列 stack_visit の全要素に対して順番に処理を繰り返しています。[イ]に代入されることとなる stack_visit[k] は、スタック内のk番目の座標情報を示していますから、
paths[sol_num][0] ← stack_visit[0]
paths[sol_num][1] ← stack_visit[1]
paths[sol_num][2] ← stack_visit[2]
というように、paths[sol_num]の0からk番目の位置に順に代入すれば、stack_visit に格納されている解の情報を paths[sol_num] にコピーすることができます。したがって、添字vにはループ変数であるkを使うのが適切です。paths[sol_num][1] ← stack_visit[1]
paths[sol_num][2] ← stack_visit[2]
∴イ=paths[sol_num][k]
〔ウについて〕
空欄ウを含む23行目の処理は、訪問先が終点ではない場合の最後に実行される処理です。
else節内の処理を初めから順に追っていくと、10行目で変数 stack_top が1加算されています。これはもし上下左右いずれかのマスに移動した場合、移動先のマスに対する関数 visit の最初でスタックに座標を積む処理があるため、移動前にあらかじめスタックの最後尾を1つ後ろにずらしておく意味合いがあります。
そして11~22行目では、上⇒右⇒下⇒左の順に4方向へ"進む"試みを行っています。もし移動可能であれば移動先のマスに対して関数 visit が呼び出されますし、移動不可であれば何もせずに次の処理に移る形です。
最後に、23行目で変数 stack_top への代入処理が行われています。
23行目が実行されるのは、4方向すべてのマスがOKフラグではなく(訪問済・壁・障害物マスのいずれかで)先に"進む"ことができないときです。10行目でスタックの最後尾を1つ後ろにずらしたのは、"進む"ことを前提としたものなので、先に進めないときにはスタックの最後尾を元に戻しておかなければなりません。他に変数 stack_top に代入する処理はないので、23行目でそれを元に戻す、すなわち変数 stack_top を1減算する必要があります。この処理がないと、現在処理中のマスがスタック上の経路から取り除かれないため正しい解となりません。
∴ウ=stack_top - 1
〔エについて〕
空欄エのある25行目はif文の外にあるので、終点に到達したかどうかにかかわらず実行される処理です。
仮に終点に到達していない場合、25行目は4方向へ"進む"試みを行ったあとに実行されます。〔迷路の解を見つける探索〕の「4方向いずれにも"進む"ことができないときには,現在いるマスのマス情報をOKフラグに戻し,一つ前のマスに"戻る"」という説明より、25行目の処理は「現在いるマスのマス情報をOKフラグにする」であると推測できます。終点に到達した場合も、新たな解を見つけるために終点から一つ前のマスに戻ることになるため、25行目の処理は上記の内容で問題ありません。
本問ではマス情報全体が迷路図情報と呼ばれていることから、マス情報の変更処理は表1で示されている配列 maze[x][y] に対して行えばよいとわかります。2行目で"訪問"した際に maze[x][y] に VISITED を設定していること、3行目でスタックに入れている座標が(x,y)であることから、現在いるマスは(x,y)で表せることがわかります。したがって、OKフラグの設定先は maze[x][y] となります。
∴エ=maze[x][y]
広告
設問3
図4中のオに入れる適切な字句を答えよ。
解答例・解答の要点
オ:sol_num
解説
〔オについて〕図4を確認すると、7行目のif文の条件式が真の場合、"迷路は見つからなかった"と印字する処理が実行され、逆に偽の場合、解を格納した配列 paths を印字する処理が実行されます。これより、7行目の条件式には「解が見つかっていない」ときに真となる式が当てはまると判断できます。すべてのマスの探索が終了したとき、見つかった解の個数は変数 sol_num に格納されており、解が見つからなければ変数 sol_num は初期値である0のままです。したがって、条件式としては「sol_num が0と等しい」という形になります。
表1において、整数型の変数は stack_top または sol_num しかありませんが、stack_top は探索が終了したとき常に0になっているので、解が見つかったかどうかの判定に使うことはできません。
∴オ=sol_num
広告
設問4
〔解が複数ある迷路〕について答えよ。
- 本文中の力に入れる適切な引数を答えよ。
- 本文中のキ,クに入れる適切な数値を答えよ。
解答例・解答の要点
- カ:5,3
- キ:22
ク:3
解説
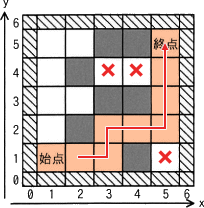
- 〔カについて〕
これまで検討した処理の流れを踏まえると、図2において最初に確定する解は以下の経路です。終点に到達する visit(5,5) の呼出しは、解を配列 paths に格納し、(5,5)にOKフラグを設定した後、呼出し元の visit(5,4) に戻ります。visit(5,4)では上方向の探索(図3の11~13行目)が終わったので、右方向に進もうとしますが右のマスは壁でNGフラグなので進むことができません(図3の14~16行目)。次に下方向に進むことを試み、下のマスがOKマスなので visit(5,3) を呼び出して下方向に移動することになります(図3の17~19行目)。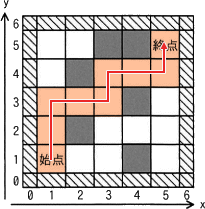 ∴カ=5,3
∴カ=5,3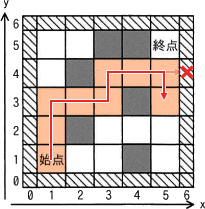
- 〔キクについて〕
上⇒右⇒下⇒左の進行順序および訪問済マス(VISITEDフラグ)のマスには進入できないことを考慮すると、2つ目の解を見つけるまでの探索は以下のように進みます。空欄クの解答で着目すべき(4,2)は赤枠で示してあります。- (5,3)から(5,1)に進む(2回)。
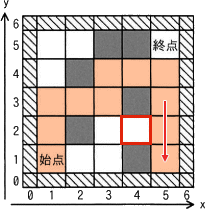
- (5,1)から(5,2)に戻る(1回)。
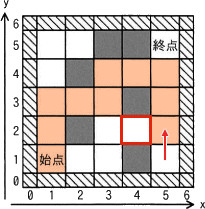
- (5,2)から(3,2)を経由して(2,1)まで進む(4回)。
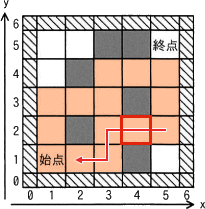
- (2,1)から(3,3)まで戻る(9回)。
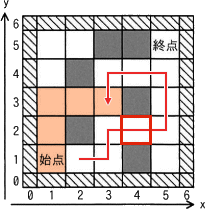
- (3,3)から(3,2)および(5,2)を経由して終点(5,5)まで進む(6回)。
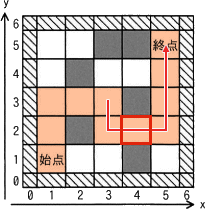
∴キ=22
ク=3 - (5,3)から(5,1)に進む(2回)。
広告

広告