令和5年春期試験午後問題 問3
問3 プログラミング
⇱問題PDF
多倍長整数の演算に関する次の記述を読んで,設問に答えよ。
多倍長整数の演算に関する次の記述を読んで,設問に答えよ。
広告
コンピュータが一度に処理できる整数の最大桁には,CPUが一度に扱える情報量に依存した限界がある。一度に扱える桁数を超える演算を行う一つの方法として10を基数とした多倍長整数(以下,多倍長整数という)を用いる方法がある。
〔多倍長整数の加減算〕
多倍長整数の演算では,整数の桁ごとの値を,1の位から順に1次元配列に格納して管理する。例えば整数123は,要素数が3の配列に{3,2,1}を格納して表現する。
多倍長整数の加算は,"桁ごとの加算"の後,"繰り上がり"を処理することで行う。456+789を計算した例を図1に示す。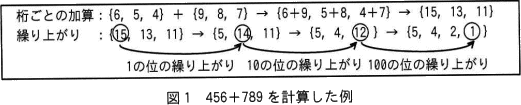 "桁ごとの加算"を行うと,配列の内容は{15,13,11}となる。1の位は15になるが,15は10×1+5なので,10の位である13に1を繰り上げて{5,14,11}とする。これを最上位まで繰り返す。最上位で繰り上がりが発生する場合は,配列の要素数を増やして対応する。減算も同様に"桁ごとの減算"と"繰り下がり"との処理で計算できる。
"桁ごとの加算"を行うと,配列の内容は{15,13,11}となる。1の位は15になるが,15は10×1+5なので,10の位である13に1を繰り上げて{5,14,11}とする。これを最上位まで繰り返す。最上位で繰り上がりが発生する場合は,配列の要素数を増やして対応する。減算も同様に"桁ごとの減算"と"繰り下がり"との処理で計算できる。
〔多倍長整数の乗算〕
多倍長整数の乗算については,計算量を削減するアルゴリズムが考案されており,その中の一つにカラツバ法がある。ここでは,桁数が2のべき乗で,同じ桁数をもった正の整数同士の乗算について,カラツバ法を適用した計算を行うことを考える。桁数が2のべき乗でない整数や,桁数が異なる整数同士の乗算を扱う場合は,上位の桁を0で埋めて処理する。例えば,123×4は0123×0004として扱う。
〔ツリー構造の構築〕
カラツバ法を適用した乗算のアルゴリズムは,計算のためのツリー構造(以下,ツリーという)を作る処理と,ツリーを用いて演算をする処理から成る。ツリーは,多倍長整数の乗算の式を一つのノードとし,一つのノードは3個の子ノードをもつ。
M桁×M桁の乗算の式について,乗算記号の左右にある値を,それぞれM/2桁ずつに分けてA,B,C,Dの四つの多倍長整数を作る。これらの整数を使って,①A×C,②B×D,③(A+B)×(C+D)の3個の子ノードを作り,M/2桁×M/2桁の乗算を行う層を作る。(A+B),(C+D)は多倍長整数の加算の結果であるが,ここでは "桁ごとの加算"だけを行い,"繰り上がり"の処理はツリーを用いて行う演算の最後でまとめて行う。生成した子ノードについても同じ手順を繰り返し,1桁×1桁の乗算を行う最下層のノードまで展開する。
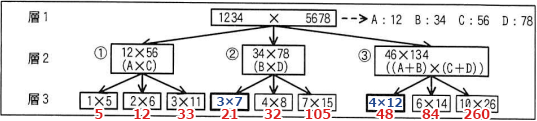
1234×5678についてのツリーを図2に示す。図2の層2の場合,①は12×56,②は34×78,③は46×134となる。③の(C+D)は,"桁ごとの加算"だけの処理を行うと,10の位が5+7=12,1の位が6+8=14となるので,12×10+14=134となる。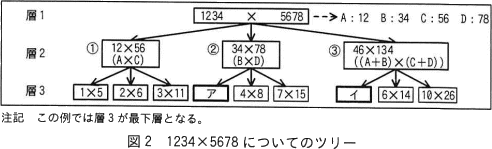 〔ツリーを用いた演算〕
〔ツリーを用いた演算〕
ツリーの最下層のノードは,整数の乗算だけで計算できる。最下層以外の層は,子ノードの計算結果を使って,次の式で計算できることが分かっている。ここで,α,β,γは,それぞれ子ノード①,②,③の乗算の計算結果を,Kは対象のノードの桁数を表す。
桁数が2のべき乗の多倍長整数val1,val2の乗算を行うプログラムを作成した。
プログラム中で利用する多倍長整数と,ツリーのノードは構造体で取り扱う。構造体の型と要素を表1に示す。構造体の各要素には,構造体の変数名.要素名でアクセスできる。また,配列の添字は1から始まる。 多倍長整数の操作を行う関数を表2に,プログラムで使用する主な変数,配列及び関数を表3,与えられた二つの多倍長整数からツリーを構築するプログラムを図3に,そのツリーを用いて演算を行うプログラムを図4に,それぞれ示す。表2,表3中のp,g,v1,v2の型は多倍長整数である。また,図3,図4中の変数は全て大域変数である。
多倍長整数の操作を行う関数を表2に,プログラムで使用する主な変数,配列及び関数を表3,与えられた二つの多倍長整数からツリーを構築するプログラムを図3に,そのツリーを用いて演算を行うプログラムを図4に,それぞれ示す。表2,表3中のp,g,v1,v2の型は多倍長整数である。また,図3,図4中の変数は全て大域変数である。

〔多倍長整数の加減算〕
多倍長整数の演算では,整数の桁ごとの値を,1の位から順に1次元配列に格納して管理する。例えば整数123は,要素数が3の配列に{3,2,1}を格納して表現する。
多倍長整数の加算は,"桁ごとの加算"の後,"繰り上がり"を処理することで行う。456+789を計算した例を図1に示す。

〔多倍長整数の乗算〕
多倍長整数の乗算については,計算量を削減するアルゴリズムが考案されており,その中の一つにカラツバ法がある。ここでは,桁数が2のべき乗で,同じ桁数をもった正の整数同士の乗算について,カラツバ法を適用した計算を行うことを考える。桁数が2のべき乗でない整数や,桁数が異なる整数同士の乗算を扱う場合は,上位の桁を0で埋めて処理する。例えば,123×4は0123×0004として扱う。
〔ツリー構造の構築〕
カラツバ法を適用した乗算のアルゴリズムは,計算のためのツリー構造(以下,ツリーという)を作る処理と,ツリーを用いて演算をする処理から成る。ツリーは,多倍長整数の乗算の式を一つのノードとし,一つのノードは3個の子ノードをもつ。
M桁×M桁の乗算の式について,乗算記号の左右にある値を,それぞれM/2桁ずつに分けてA,B,C,Dの四つの多倍長整数を作る。これらの整数を使って,①A×C,②B×D,③(A+B)×(C+D)の3個の子ノードを作り,M/2桁×M/2桁の乗算を行う層を作る。(A+B),(C+D)は多倍長整数の加算の結果であるが,ここでは "桁ごとの加算"だけを行い,"繰り上がり"の処理はツリーを用いて行う演算の最後でまとめて行う。生成した子ノードについても同じ手順を繰り返し,1桁×1桁の乗算を行う最下層のノードまで展開する。
1234×5678についてのツリーを図2に示す。図2の層2の場合,①は12×56,②は34×78,③は46×134となる。③の(C+D)は,"桁ごとの加算"だけの処理を行うと,10の位が5+7=12,1の位が6+8=14となるので,12×10+14=134となる。

ツリーの最下層のノードは,整数の乗算だけで計算できる。最下層以外の層は,子ノードの計算結果を使って,次の式で計算できることが分かっている。ここで,α,β,γは,それぞれ子ノード①,②,③の乗算の計算結果を,Kは対象のノードの桁数を表す。
α×10K+(γ-α-β)×10K/2+β ……(1)
図2のルートノードの場合,K=4,α=672,β=2652,γ=6164なので,計算結果は次のとおりとなる。672×10000+(6164-672-2652)×100+2652=7006652
〔多倍長整数の乗算のプログラム〕桁数が2のべき乗の多倍長整数val1,val2の乗算を行うプログラムを作成した。
プログラム中で利用する多倍長整数と,ツリーのノードは構造体で取り扱う。構造体の型と要素を表1に示す。構造体の各要素には,構造体の変数名.要素名でアクセスできる。また,配列の添字は1から始まる。



広告
設問1
図2中のア,イに入れる適切な字句を答えよ。
解答例・解答の要点
ア:3×7
イ:4×12
イ:4×12
解説
〔アについて〕34と78をぞれぞれM/2桁=1桁ずつに分けてA、B、C、Dの4つの多倍長整数で表現すると、次のようになります。
- A … 3 = {3}
- B … 4 = {4}
- C … 7 = {7}
- D … 8 = {8}
∴ア=3×7
〔イについて〕
上記と同じく、46と134をA、B、C、Dの4つの多倍長整数で表現していきますが、「(A+B),(C+D) は…"桁ごとの加算"だけを行い,"繰り上がり"の処理はツリーを用いて行う演算の最後でまとめて行う」という説明に注意します。
層1から層2③のノードを作るところから考えると、1234と5678は、
- A … 12 = {2, 1}
- B … 34 = {4, 3}
- C … 56 = {6, 5}
- D … 78 = {8, 7}
- A+B = {2+4, 1+3} = {6, 4}
- C+D = {6+8, 5+7} = {14, 12} //繰り上がりはない
これを踏まえて、46と134をM/2桁=1桁ずつに分けてA、B、C、Dの4つの多倍長整数で表現すると、次のようになります。
- A … 4 = {4}
- B … 6 = {6}
- C … 12 = {12}
- D … 14 = {14}
∴イ=4×12
広告
設問2
図2中の層2にある46×134のノードについて,本文中の式(1)の数式は具体的にどのような計算式になるか。次の式の①~④に入れる適切な整数を答えよ。
( ① )×100+(( ② )-( ③ )-84)×10+( ④ )
解答例・解答の要点
①:48
②:260
③:48
④:84
②:260
③:48
④:84
解説
本文中の式(1)と設問2の式を比較すると、①とα、②とγ、③とα、④とβがそれぞれ対応しています。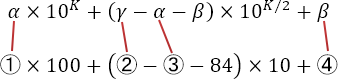
- α(子ノード①の計算結果)4×12=48
- β(子ノード②の計算結果)6×14=84
- γ(子ノード③の計算結果)10×26=260
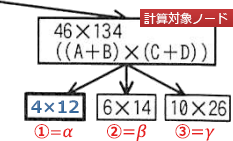
∴①=48、②=260、③=48、④=84
広告
設問3
図3中のウ~カに入れる適切な字句を答えよ。
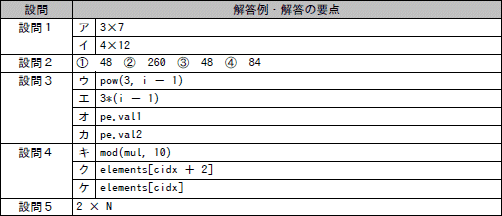
解答例・解答の要点
ウ:pow(3,i-1)
エ:3*(i-1)
オ:pe.val1 ※順不同
カ:pe.val2 ※順不同
エ:3*(i-1)
オ:pe.val1 ※順不同
カ:pe.val2 ※順不同
解説
解説の便宜上、図3のプログラムに行番号を振っておきます。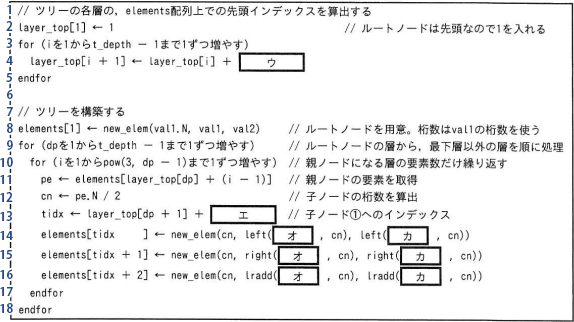
配列 elements は、ルートノードを先頭に、各層の左側から順にノードを格納した配列です。配列 layer_top は、各層の左端ノードの、配列 elements 上での添字の値を保持する配列ですから、図2の場合、配列 layer_top の各要素には{1, 2, 5}が設定されます。
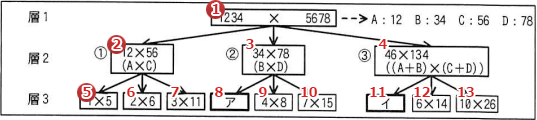
- i=1 → 1 + 1 = 2
- i=2 → 2 + 3 = 5
- i=3 → 5 + 9 = 14
各ノードは3個の子ノードを持つので、層2のノードの個数は「3個」、層3は「3×3=9個」、層4は「3×3×3=27個」、…と1層下がるごとに3倍ずつ増えていきますから、層iのノードの数(赤太字の数)は 3i-1 の式で表すことができます。これを層iの左端ノードの添字に加算すれば、ひとつ下の層の左端ノードの添字となります。累乗は表3の関数 pow(m, k) を用いて記述できるので、答えは「pow(3, i-1)」です。
∴ウ=pow(3,i-1)
〔エについて〕
ツリーを構築する部分は、ルートノードの層から最下層以外の層まで順に、ノードごと3つの子ノードを作っていく処理です。10~18行目の入れ子になったfor文はそれぞれ次のような繰返しを行います。変数 dp は、現在の層の番号、変数 i は各層上のノードの番号を示しています。
//ルートノードの層から最下層以外の層まで順に繰り返す
for (dpを1からt_depth-1まで1ずつ増やす)
//1から各層のノード数まで順に繰り返す
for (iを1からpow(3, dp-1)まで1ずつ増やす)
変数 tidx は、コメント部にあるように「子ノード①へのインデックス」、すなわち子ノード①の配列 elements 上の添字ですから、図2において層2から層3を作るときのことを考えると、dp、i および tidx は次のように対応します。for (dpを1からt_depth-1まで1ずつ増やす)
//1から各層のノード数まで順に繰り返す
for (iを1からpow(3, dp-1)まで1ずつ増やす)
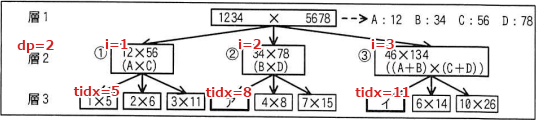
- i=1のとき layer_top[dp+1](上図では5+0=5)
- i=2のとき layer_top[dp+1] + 3(上図では5+3=8)
- i=3のとき layer_top[dp+1] + 6(上図では5+6=11)
∴エ=3*(i-1)
〔オカについて〕
〔ツリー構造の構築〕の説明を踏まえると、14~16行目は3つの子ノードを作成する処理に当たることがわかります。14行目が子ノード①、15行目が②、16行目が③を作成する処理です。空欄は共通しているので14行目に着目して考えていきます。
子ノードの生成に使われている関数 new_elem の説明より、14行目のnew_elem(cn, left([オ], cn), left([カ], cn))は、「取り扱う多倍長整数の桁数がcnで、left([オ], cn) の値と left([カ], cn) の値の乗算を表すノード」を作成するという意味になります。子ノード①は〔ツリー構造の構築〕でいうところの「A×C」なので、left([オ], cn)はA、left([カ], cn)はCに相当することになります。関数 left(p, k) は「多倍長整数 p の上位 k 桁を返す」関数であり、第2引数に指定されている変数 cn には、12行目で「子ノードの桁数(=親ノードの桁数Mの1/2)」が格納されていますから、第1引数である空欄オ・カには多倍長整数を指定すべきであることがわかります。
〔ツリー構造の構築〕の説明に沿ってAとCを言い換えると、Aは「親ノードの乗算記号の左の値の左半分(上位M/2桁)」、Cは「親ノードの乗算記号の右の値の左半分(上位M/2桁)」と言い表すことができます。左半分の指定は変数 cn によって行われているので、空欄オには「親ノードの乗算記号の左の値」、空欄カには「親ノードの乗算記号の右の値」を示す式を入れればよいことになります。
親ノードは11行目より変数 pe として表現されており、pe には配列 elements 上の要素が代入されています。表3より、配列 elements の型は"ノード"なので、変数 pe の型も"ノード"です。構造体"ノード"について表1で確認すると、構造体"ノード"は要素として乗算記号の左側の値を val1、右側の値を val2 として保持していることがわかります。構造体の要素は「構造体の変数名.要素名」でアクセスするため、親ノードの左側の値は pe.val1、親ノードの右側の値は pe.val2 で参照できます。したがって、空欄オには「pe.val1」、空欄カには「pe.val2」がそれぞれ当てはまります。
なお、乗算記号の左右の値が逆になっても最終的な結果は正しいものとなるので、空欄オに「pe.val2」、空欄カに「pe.val1」を入れても正解となります。
∴オカ=pe.val1、pe.val2
広告
設問4
図4中のキ~ケに入れる適切な字句を答えよ。
解答例・解答の要点
キ:mod(mul,10)
ク:elements[cidx+2]
ケ:elements[cidx]
ク:elements[cidx+2]
ケ:elements[cidx]
解説
解説の便宜上、プログラムに行番号を振っておきます。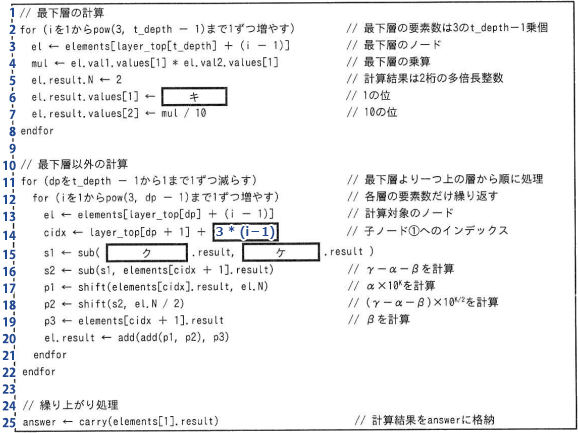
2~8行目までのfor文は、最下層のノード(1桁×1桁)ごとに左の値と右の値を乗算し、その結果を構造体"ノード"の result に格納しています。図2に対応させると、以下のような処理が行われることになります。
左の値と右の値の乗算結果は、変数 mul に格納されているので、その1の位を求めるには、mul を10で割った余りを計算することになります。表3には、剰余を求める関数 mod(m, k) が定義されていますから、これを使用して「mod(mul, 10)」とすれば、1の位を求めることができます。
∴キ=mod(mul, 10)
〔クケについて〕
2~8行目までのfor文は、最下層以外の層について子ノード①②③の計算結果を使って、〔ツリーを用いた演算〕(1)の式で計算する部分です。15~20行目の一連の処理が下記の式の計算に対応しています。
α×10K+(γ-α-β)×10K/2+β ……(1)
16行目のコメントに「γ-α-βを計算」とある点、多倍長整数同士の減算を行う関数 sub が使われていて、上の式中で減算を行うのは γ-α-β の部分しかないことから、15~16行目は「γ-α-β」を計算する処理であると当たりを付けることができます。関数 sub が2回記述されているので、15行目が「γ-α」に対応し、16行目は「γ-α」の結果(変数 s1)からβを減算していることになります。前述のように、αは子ノード①、βは子ノード②、γは子ノード③の計算結果を表します。現在処理中のノードの、子ノード①の配列 elements 上の添字は、変数 cidx に格納されているので、cidx を基点にして、子ノード①は elements[cidx]、子ノード②は elements[cidx+1]、子ノード③は elements[cidx+2] で参照することができます。
15行目で行いたい処理は「γ-α」なので、空欄クには子ノード③を参照する elements[cidx+2] が、空欄ケには子ノード①を参照する elements[cidx] が当てはまります。
∴ク=elements[cidx+2]
ケ=elements[cidx]
広告
設問5
N桁同士の乗算をする場合,多倍長整数の構造体において,配列 values に必要な最大の要素数は幾つか。Nを用いて答えよ。
解答例・解答の要点
2×N
解説
配列 values は、多倍長整数を整数の1次元配列として表現したものです。配列の各要素で各桁の値を保持しているので、多倍長整数の桁数と同じだけの要素数が必要となります。図4の最終行でルートノードの乗算結果を繰り上がり処理することにより、多倍長整数の桁数は、通常の10進数で表した整数の桁数と等しくなります。N桁の最大数同士で乗算した場合、N=1では「9×9=81」、N=2では「99×99=9801」、…というように、桁数はNの2倍になります。したがって、N桁同士の計算において配列 values に必要な最大の要素数もNの2倍です。したがって答えは「2×N」となります。
∴2×N
広告
広告