分野 ：テクノロジ系
中分類：アルゴリズムとプログラミング
小分類：データ構造

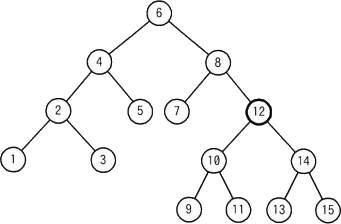
2分探索木は、2分木の各節にデータをもたせることで探索を行えるようにした木構造です。各節がもつデータは「その節から出る左部分木にあるどのデータよりも大きく、右部分木のどのデータよりも小さい」という性質があり、これを利用して効率的なデータ探索を可能にしています。

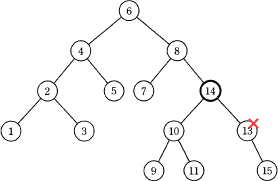
設問の2分探索木から要素12が削除された際、2分探索木の性質（要素同士の大小関係）を保つためには、12に最も近い値である要素11または要素13を新たな節点とします。この方法により他の要素の移動することなく2分探索木が再構成されます。したがって「ウ」の13が正解となります。

• 
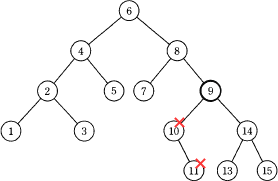
  節点である要素9の左部分木に、節点より大きい要素10と要素11が配置されるので不適切です。
• 
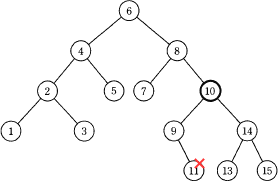
  節点である要素10の左部分木に、節点より大きい要素11が配置されるので不適切です。
• 
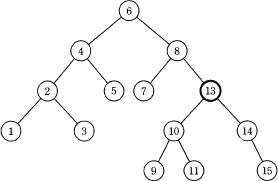
  正しい。節点である要素13の左部分木に要素9、要素10、要素11、右部分木に要素14、要素15が配置されることになるので適切です。
• 
  節点である要素14の右部分木に、節点より小さい要素13が配置されるので不適切です。