令和6年春期試験問題 午前問5
問5解説へ
正の整数Mに対して,次の二つの流れ図に示すアルゴリズムを実行したとき,結果xの値が等しくなるようにしたい。aに入れる条件として,適切なものはどれか。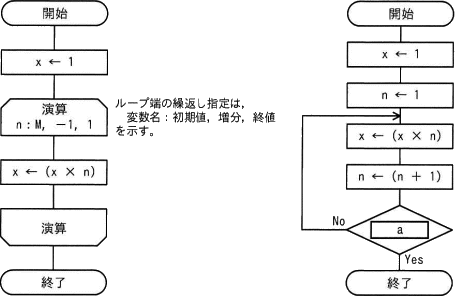

- n < M
- n > M-1
- n > M
- n > M+1
広告
解説
2つのアルゴリズムで共通の M は正の整数という条件が問題文に示されているので、Mに適当な数値を当てはめることで解答を導いていきます。正の整数であれば何でもいいのですが、本解説では M に2を代入してみます。解き方としては、まず左のアルゴリズムを解き、その結果の x の値が右の式でも出力される条件はどれかを考えていくことになります。
[左の流れ図]
[左の流れ図]
- 《開始》
- 1 → x //x=1
- 《ループ条件》n:2、増分 -1、n=1で終了
- (n=2)1×2 → x //x=2
- (n=1)ループから抜ける
- 《終了》//x=2
- 《開始》
- 1 → x //x=1
- 1 → n //n=1
- 1×1 → x //x=1
- 1+1 → n //n=2
- n=2、M=2なので、2<2⇒Noでループ先頭へ戻る。以後ループ内でnの値は1ずつ加算されていくので、n<M の条件を満たすことは永遠にありません。このため、無限ループとなってしまいます。
- n=2、M=2なので、2>2-1⇒Yesでループから抜ける。 結果xの値は1で、左の流れ図とは異なる値となります。よって、条件式として不適切です。
- n=2、M=2なので、2>2⇒Noでループ先頭へ戻る //x=1
- 1×2 → x //x=2
- 2+1 → n //n=3
- n=3、M=2なので、3>2⇒Yesでループから抜ける //x=2
- n=2、M=2なので、2>2+1⇒Noでループ先頭へ戻る //x=1
- 1×2 → x //x=2
- 2+1 → n //n=3
- n=3、M=2なので、3>2+1⇒Noでループ先頭へ戻る //x=2
- 2×3 → x //x=6
- 3+1 → n //n=4
- n=4、M=2なので、4>2+1⇒Yesでループから抜ける //x=6
広告