平成18年春期試験問題 午前問3
問3解説へ
0以上255以下の整数nに対して,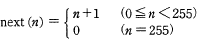 と定義する。next(n)と恒等的に等しい式はどれか。ここで,x AND y 及び x OR y は,それぞれxとyを2進数表現にして,けたごとの論理積及び論理和をとったものとする。
と定義する。next(n)と恒等的に等しい式はどれか。ここで,x AND y 及び x OR y は,それぞれxとyを2進数表現にして,けたごとの論理積及び論理和をとったものとする。
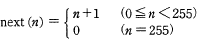
- (n+1) AND 255
- (n+1) AND 256
- (n+1) OR 255
- (n+1) OR 256
広告
解説
next(n)のとる値を考えてみると、0→1→2→3→・・・→255→0→1 というように、引数の値に1を加算した値を返し255になると0に戻る関数であると言えます。
この問題で考えなければいけないポイントは、
まず論理和(OR)演算である「ウ」と「エ」は、常に結果が同じ値(「ウ」は 255、「エ」は 256)となってしまうので正しくないことがわかります。
残った論理積(AND)演算である「ア」と「イ」ですが、「イ」を2進数で表すと 1 0000 0000となり、下位8ビットの演算結果は常に0になることがわかります。
つまり「イ」は間違いで、正しく結果が返されるのは「ア」だけということになります。下は「ア」の式のビット演算図です。
この問題で考えなければいけないポイントは、
- 1ずつの加算がおこなわれるか。
- next(255)のときに結果が 0となるか。
まず論理和(OR)演算である「ウ」と「エ」は、常に結果が同じ値(「ウ」は 255、「エ」は 256)となってしまうので正しくないことがわかります。
残った論理積(AND)演算である「ア」と「イ」ですが、「イ」を2進数で表すと 1 0000 0000となり、下位8ビットの演算結果は常に0になることがわかります。
つまり「イ」は間違いで、正しく結果が返されるのは「ア」だけということになります。下は「ア」の式のビット演算図です。

広告