平成18年春期試験問題 午前問33
問33解説へ
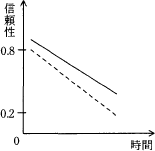
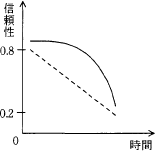
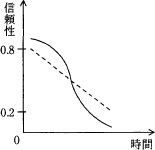
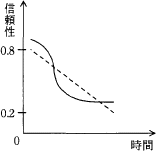
3個の構成要素のうち2個以上が正常ならば正しい結果が得られるようなシステムにおいて，個々の構成要素の信頼性が時間の経過とともに破線のグラフで示すように低下する場合，システム全体の信頼性の変化の傾向を表す実線のグラフとして適切なものはどれか。
広告
解説
3つの構成要素がとり得る状態の組合せは以下のように(23=)8通りあり、そのうち正常(○)が2つ以上である4通りの場合に正しい結果が得られることになります。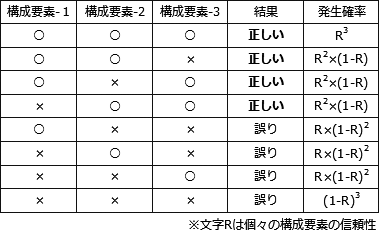
それぞれのケースは上記の確率で発生するので、構成要素の信頼度が(グラフの目盛になっている)0.8、および0.2である場合についてのシステム全体の信頼度を計算します。
[信頼度が0.8の場合]
0.8×0.8×0.8＝0.512
0.8×0.8×0.2＝0.128
0.8×0.2×0.8＝0.128
0.2×0.8×0.8＝0.128
システム全体として正しい結果が得られる確率は4つのケースを足し合わせた値なので、
0.512＋0.128×3＝0.896
[信頼度が0.2の場合]
0.2×0.2×0.2＝0.008
0.2×0.2×0.8＝0.032
0.2×0.8×0.2＝0.032
0.8×0.2×0.2＝0.032
正しい結果が得られる確率は、
0.008＋0.032×3＝0.104
さらに中間値である0.5の場合では、
[信頼度が0.5の場合]
0.5×0.5×0.5＝0.125
0.5×0.5×0.5＝0.125
0.5×0.5×0.5＝0.125
0.5×0.5×0.5＝0.125
正しい結果が得られる確率は、
0.125×4＝0.5
この計算結果から、このシステムでは構成要素の信頼度が0.5よりも大きければ全体の信頼性は個々の構成要素よりも大きくなり、0.5よりも小さければ全体の信頼性は個々の構成要素よりも小さくなることがわかります。したがってこの関係を適切に表している「ウ」のグラフが正解となります。
[信頼度が0.8の場合]
0.8×0.8×0.8＝0.512
0.8×0.8×0.2＝0.128
0.8×0.2×0.8＝0.128
0.2×0.8×0.8＝0.128
システム全体として正しい結果が得られる確率は4つのケースを足し合わせた値なので、
0.512＋0.128×3＝0.896
[信頼度が0.2の場合]
0.2×0.2×0.2＝0.008
0.2×0.2×0.8＝0.032
0.2×0.8×0.2＝0.032
0.8×0.2×0.2＝0.032
正しい結果が得られる確率は、
0.008＋0.032×3＝0.104
さらに中間値である0.5の場合では、
[信頼度が0.5の場合]
0.5×0.5×0.5＝0.125
0.5×0.5×0.5＝0.125
0.5×0.5×0.5＝0.125
0.5×0.5×0.5＝0.125
正しい結果が得られる確率は、
0.125×4＝0.5
この計算結果から、このシステムでは構成要素の信頼度が0.5よりも大きければ全体の信頼性は個々の構成要素よりも大きくなり、0.5よりも小さければ全体の信頼性は個々の構成要素よりも小さくなることがわかります。したがってこの関係を適切に表している「ウ」のグラフが正解となります。
広告