分野：テクノロジ系
中分類：アルゴリズムとプログラミング
小分類：データ構造

問題文にある「葉以外の節点はすべて二つの子をもち，根から葉までの深さがすべて等しい木」は次のような構造をもつ木です。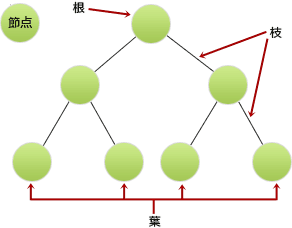この木構造をもとに、すべての選択肢を検証してみます。

• 枝の個数は「6」，葉を含む節点の個数は「7」で一致しないので誤りです。
• 木の深さは「2」，葉の個数は「4」です。2^n-1のnに木の深さ「2」を代入すると、
  　2^2-1＝2¹＝2
  となり葉の個数「4」と一致しないので誤りです。
• 葉を含む節点の個数は「7」で、木の深さは「2」です。log₂nのnに節点の個数「7」を代入すると、
  　log₂7＝2.807…
  木の深さ「2」と一致しないので誤りです。
  
  完全2分木では深さが1つ増える毎に節点の個数は次のように増加していきます。
  
  (根のみ) 1
  (深さ1) 1＋2＝3
  (深さ2) 1＋2＋4＝7
  (深さ3) 1＋2＋4＋8＝15
  (深さ4) 1＋2＋4＋8＋16＝31
  (深さ5) 1＋2＋4＋8＋16＋32＝63
  
  このため節点の個数がnである完全2分木の深さは「log₂(n＋1)－1」の式で表すことができます。
• 葉の数は「4」，葉以外の節点には根が含まれるので「3」です。
  葉の数をnとすると、葉以外の節点の数はn－1になっています。したがってこの記述が適切です。

「葉以外の節点はすべて二つの子をもち，根から葉までの深さがすべて等しい木」は完全2分木と呼ばれ、木の深さが「n」であれば葉の数は「2ⁿ」、葉の数が「n」であれば、葉以外の節点の数(根を含む)は「n－1」であるという特徴を持っています。