平成21年春期試験午後問題 問2
問2 プログラミング
⇱問題PDF
探索アルゴリズムであるハッシュ法の一つ，チェイン法に関する次の記述を読んで，設問1～4に答えよ。
探索アルゴリズムであるハッシュ法の一つ，チェイン法に関する次の記述を読んで，設問1～4に答えよ。
広告
配列に対して，データを格納すべき位置(配列の添字)をデータのキーの値を引数とする関数(ハッシュ関数)で求めることによって，探索だけではなく追加や削除も効率よく行うのがハッシュ法である。
通常，キーのとり得る値の数に比べて，配列の添字として使える値の範囲は狭いので，衝突(collision)と呼ばれる現象が起こり得る。衝突が発生した場合の対処方法の一つとして，同一のハッシュ値をもつデータを線形リストによって管理するチェイン法(連鎖法ともいう)がある。
8個のデータを格納したときの例を図1に示す。
このとき，キー値は正の整数，配列の添字は0～6の整数，ハッシュ関数は引数を7で割った剰余を求める関数とする。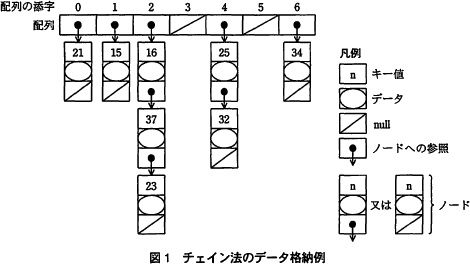
このチェイン法を実現するために表に示す構造体配列及び関数を使用する。
構造体を参照する変数からその構造体の構成要素へのアクセスには"."を用いる。例えば，図1のキー値 25 のデータは table[4].data でアクセスできる。また，構造体の実体を生成するには，次のように書き，生成された構造体への参照が値になる。
new Node(key，data，nextNode)
〔探索関数 search〕
探索のアルゴリズムを実装した関数 search の処理手順を次の(1)～(3)に，そのプログラムを図2に示す。
〔追加関数 addNode〕
データの追加手続を実装した関数 addNode の処理手順を次の(1)～(3)にプログラムを図3に示す。図3中のア，イには，図2中のア，イと同一のものが入る。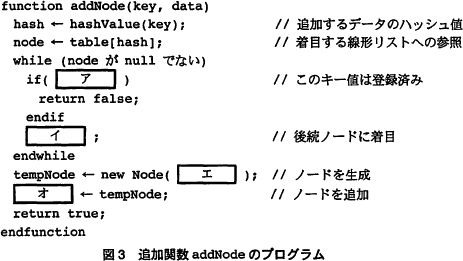
〔チェイン法の計算量〕
チェイン法の計算量を考える。
計算量が最悪になるのは，カ場合である。しかし，ハッシュ関数の作り方が悪くなければ，このようなことになる確率は小さく，実際上は無視できる。
チェイン法では，データの個数をnとし，表の大きさ(配列の長さ)をmとすると，線形リスト上の探索の際にアクセスするノードの数は，線形リストの長さの平均n／mに比例する。mの選び方は任意なので，nに対して十分に大きくとっておけば，計算量がキとなる。この場合の計算量は2分探索木によるO(log n)より小さい。
通常，キーのとり得る値の数に比べて，配列の添字として使える値の範囲は狭いので，衝突(collision)と呼ばれる現象が起こり得る。衝突が発生した場合の対処方法の一つとして，同一のハッシュ値をもつデータを線形リストによって管理するチェイン法(連鎖法ともいう)がある。
8個のデータを格納したときの例を図1に示す。
このとき，キー値は正の整数，配列の添字は0～6の整数，ハッシュ関数は引数を7で割った剰余を求める関数とする。
new Node(key，data，nextNode)
〔探索関数 search〕
探索のアルゴリズムを実装した関数 search の処理手順を次の(1)～(3)に，そのプログラムを図2に示す。
- 探索したいデータのキー値からハッシュ値を求める。
- ハッシュ表中のハッシュ値を添字とする要素が参照する線形リストに着目する。
- 線形リストのノードに先頭から順にアクセスする。キー値と同じ値が見つかれば，そのノードに格納されたデータを返す。末尾まで探して見つからなければ null を返す。
データの追加手続を実装した関数 addNode の処理手順を次の(1)～(3)にプログラムを図3に示す。図3中のア，イには，図2中のア，イと同一のものが入る。
- 追加したいデータのキー値からハッシュ値を求める。
- ハッシュ表中のハッシュ値を添字とする要素が参照する線形リストに着目する。
- 線形リストのノードに先頭から順にアクセスする。キー値と同じ値が見つかれば，キー値は登録済みであり追加失敗として false を返す。末尾まで探して見つからなければ，リストの先頭にノードを追加して true を返す。
チェイン法の計算量を考える。
計算量が最悪になるのは，カ場合である。しかし，ハッシュ関数の作り方が悪くなければ，このようなことになる確率は小さく，実際上は無視できる。
チェイン法では，データの個数をnとし，表の大きさ(配列の長さ)をmとすると，線形リスト上の探索の際にアクセスするノードの数は，線形リストの長さの平均n／mに比例する。mの選び方は任意なので，nに対して十分に大きくとっておけば，計算量がキとなる。この場合の計算量は2分探索木によるO(log n)より小さい。
広告
設問1
衝突(collision)とはどのような現象か。"キー"と"ハッシュ関数"という単語を用いて，35字以内で述べよ。
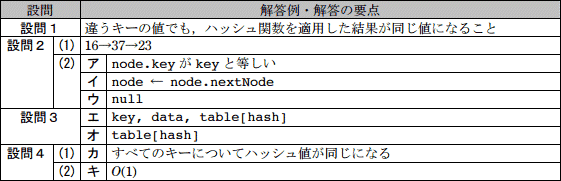
解答例・解答の要点
違うキーの値でも，ハッシュ関数を適用した結果が同じになること (30文字)
解説
ハッシュ関数で求めた値の取り得る範囲が狭い場合、値が重複してしまい、異なるデータでも格納する位置が被ってしまう、という現象が起こり得ます。このとき、異なるデータのハッシュ値が重複することを衝突と呼びます。なお、重複したデータはシノニムと呼び、衝突が起こることを「シノニムが生じる」という場合もあります。"キー"と"ハッシュ関数"という単語を用いてという条件があるので、「異なるキーのハッシュ値が同じになること」という意味の解答ができればOKです。
∴違うキーの値でも，ハッシュ関数を適用した結果が同じになること
広告
設問2
〔探索関数 search〕について，(1)，(2)に答えよ。
- 図1の場合，キー値が23のデータを探索するために，ノードにアクセスする順序はどのようになるか。"key1→key2→…→23"のように，アクセスしたノードのキー値の順序で答えよ。
- 図2中のア～ウに入れる適切な字句を答えよ。
解答例・解答の要点
- 16→37→23
- ア：node.keyがkeyと等しい
イ：node ← node.nextNode
ウ：null
解説
- 「ノードにアクセスする順序」を見いだすには、プログラムがどのように動作するのかがわかれば良いです。そこで、問題文にある探索関数 search の処理手順をたどってみましょう。
まず処理手順(1)について考えます。今回探索するデータのキー値は23、ハッシュ関数は問題文より「引数を7で割った剰余を求める関数」ですので「23÷7＝3 余り 2」より、ハッシュ値は2となります。
次に処理手順(2)について考えます。先述の通りハッシュ値は2ですから、図1のうち、配列の添字2で参照している「16→37→23」が着目する線形リストとなります。
最後に処理手順(3)について考えます。(3)には「キー値と同じ値が見つかるまで，線形リストのノードに先頭から順にアクセスする」とあります。これより、アクセスの順番は(2)で着目した線形リストの先頭から探索するキー値まで、すなわち「16→37→23」です。これが解答となります。
∴16→37→23 - 問題文にある探索関数 search の処理手順と図2のプログラムとの対応を考えます。解説の便宜上、プログラムに行番号を振っておきます。処理手順(1)は2行目と、処理手順(2)は3行目とそれぞれ対応しています。したがって、[ア]～[ウ]は処理手順(3)の処理の一部であることがわかります。
また表より、線形リストは構造体 Node を用いて実装されていることから、変数 node は構造体 Node を参照する変数です。これらを手がかりに解いていきます。
〔アについて〕
if文の条件式が入ります。条件が真となるときは node.data、つまり着目しているノードのデータを返しています。
ノードのデータを返す条件を処理手順(3)と照らし合わせて考えてみましょう。(3)には「キー値と同じ値が見つかれば，そのノードに格納されたデータを返す」とあります。よって、求める条件は「キー値と同じ値が見つかったとき」、すなわち「探索しているデータのキー値が、着目しているノードのキー値と同じとき」となります。
プログラム上では「探索しているデータのキー値」は key、「着目しているノードのキー値」は表で示されている構造体 Node の構成要素である node.key でアクセスできます。したがって、解答は「keyがnode.keyと等しいとき」となります。
∴ア＝node.keyがkeyと等しい
〔イについて〕
[イ]は5行目のif文の条件式が偽のときのみ実行される処理です。なぜならif文の内部が実行されると、return文により関数が終了するからです。これより[イ]は、探索しているキー値がまだ見つかっていないときに行う処理であることがわかります。
また、[イ]が記載されている行の「//後続ノードに着目」というコメントから、末尾まで探し終わったときの処理ではなさそうです。着目しているノードのキー値が探索しているキー値ではなかったときは、後続のノードにアクセスすることになりますから、ここには着目しているノードの後続ノードへアクセスする処理が入ることがわかります。
「着目しているノードの後続ノード」は、表で示されている構造体 Node の構成要素である node.nextNode でアクセスできます。また、後続ノードは次のwhileループで着目するノードとして扱いたいので、変数 node に代入します。したがって、解答は「node ← node.nextNode」となります。
∴イ＝node ← node.nextNode
〔ウについて〕
return文の一部ですので関数の返却値が入ります。
この行のコメントに「//探索失敗」と説明されているように、この部分までプログラムが実行されるということは、whileループで末尾ノードまで探索したにもかかわらず探索目的のキー値が見つからなかったということです。処理手順(3)には「末尾まで探して見つからなければ null を返す」とあり、これを実現する処理は他に書かれていません。したがって、return文で返すべきは「null」であると判断できます。
∴ウ＝null
広告
設問3
〔追加関数 addNode〕のプログラム，図3中のエ，オに入れる適切な字句を答えよ。
解答例・解答の要点
エ：key, data, table[hash]
オ：table[hash]
オ：table[hash]
解説
問題文にある追加関数 addNode の処理手順と図3のプログラムとの対応を考えます。解説の便宜上、プログラムに行番号を振っておきます。
図3 addNode の4～9行目は図2 search の4～9行目とよく似た処理です。これらを比較して考えると、図3の4～9行目は処理手順(3)の「線形リストのノードに先頭から順にアクセスする。キー値と同じ値が見つかれば，キー値は登録済みであり追加失敗として false を返す」に対応する処理であることがわかります。
したがって、[エ]及び[オ]を含む3行は処理手順(3)の「末尾まで探して見つからなければ，リストの先頭にノードを追加して true を返す」に対応する処理です。これを手がかりに解いていきます。
〔エについて〕
[エ]が記載されている行のコメントには「//ノードを生成」とあります。また問題文には「new Node(key，data，nextNode)」と書くことで構造体が生成ができるとあります。よって、[エ]には生成するノードの「key, data, nextNode」、つまり「キー値、データ、後続ノードへの参照」に対応する字句を入れればよいわけです。
生成するノードのキー値とデータは、関数 addNode の引数である key と data です。次に後続ノードへの参照を考えます。処理手順(3)に「リストの先頭にノードを追加して」とあるので、生成するノードがリストの先頭になるようにしなければなりません。これには後続ノードへの参照として、現在リストの先頭にあるノードを設定すればよいです。プログラムの3行目にあるように、着目するリストの先頭ノードは table[hash] で参照できるので、後続ノードへの参照に設定するのは table[hash] となります。
以上より、解答は「key, data, table[hash]」です。
∴エ＝key, data, table[hash]
〔オについて〕
[エ]でリストの先頭に追加するノード tempNode を作成しましたが、以下の例のように、まだリストに組み込まれておらずどこからも参照されない状態になっています。
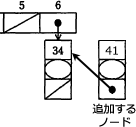
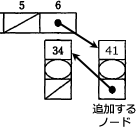
∴オ＝table[hash]
広告
設問4
〔チェイン法の計算量〕について，(1)，(2)に答えよ。
- カに入れる適切な字句を25字以内で答えよ。
- キに入れる計算量をO記法で答えよ。
解答例・解答の要点
- カ：すべてのキーについてハッシュ値が同じになる (21文字)
- キ：O(1)
解説
- 〔カについて〕
計算量とは、ある処理の計算時間がどの程度なのかを表したものです。また「計算量が最悪になる」とは、「計算時間が最も長くなる」という意味です。
探索および追加関数の処理で、計算時間に差が出るのは「線形リストのノードに先頭から順にアクセスする」部分です。これが最も遅くなるパターンを考えると、すべてのデータが一つの線形リストにまとめられる場合、すなわち「すべてのキーのハッシュ値が同じになる」場合であるとわかります。このときの計算量は O(n) です。
∴カ＝すべてのキーについてハッシュ値が同じになる - 〔キについて〕
データの個数がn、配列の長さがmのとき、線形リストの長さの平均は n／m です。データの個数nに対して配列の長さmが十分に大きく、ハッシュ関数の作り方も妥当な場合、衝突がほぼ発生しなくなり、データが格納されている箇所の線形リストの長さはほとんど1になります。この場合、探索であっても追加であってもwhileループの繰返し回数がほぼ1回で済むので、計算量は定数時間、すなわち「O(1)」となります。
∴キ＝O(1)
広告
広告