平成23年特別試験問題 午前問2
広告
解説
aの手前部分の演算は、
1101 ⊕ 0001 = 1100
また排他的論理和には、同じビット列で2回演算をすると元のビット列に戻るという特徴があるので、式の結果「1111」とその手前の「1101」の排他的論理和をとると、
1111 ⊕ 1101 = 0010
となります。計算結果を図に書き込むと以下のようになります。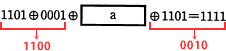 これでaの前後がわかりましたので、後は演算がつながるように、
これでaの前後がわかりましたので、後は演算がつながるように、
1100 ⊕ a=0010
が成立するビット列をaに当てはめれば良いことがわかります。
排他的論理和演算の特徴(ビットが同じなら0,異なれば1を出力)に注意して、ビット列を考えると、a=1110 となります。
1101 ⊕ 0001 = 1100
また排他的論理和には、同じビット列で2回演算をすると元のビット列に戻るという特徴があるので、式の結果「1111」とその手前の「1101」の排他的論理和をとると、
1111 ⊕ 1101 = 0010
となります。計算結果を図に書き込むと以下のようになります。

1100 ⊕ a=0010
が成立するビット列をaに当てはめれば良いことがわかります。
排他的論理和演算の特徴(ビットが同じなら0,異なれば1を出力)に注意して、ビット列を考えると、a=1110 となります。
広告