平成25年秋期試験午後問題 問2
問2 プログラミング
⇱問題PDF
リストによるメモリ管理に関する次の記述を読んで,設問1~3に答えよ。
リストによるメモリ管理に関する次の記述を読んで,設問1~3に答えよ。
広告
与えられたメモリ空間(以下,ヒープ領域という)の中に,可変長のメモリブロックを動的に割り当てるためのデータ構造及びアルゴリズムを考える。
ヒープ領域は,一つ以上の連続したメモリブロックで構成する。メモリブロックは,固定長のヘッダー部分と可変長のデータ部分で構成される。ヘッダー部分は構造体で,prev,next,status 及び size のメンバーによって構成される。メモリブロックの構造を図1に,ヘッダー部分のメンバーの意味を表1にそれぞれ示す。メモリブロックを指すポインタ変数には,メモリブロックの先頭アドレスをセットする。あるメモリブロックを指すポインタ変数を q とするとき,そのメンバー prev の参照は,q->prevと表記する。また,ヘッダー部分のバイト数は,HSIZE とする。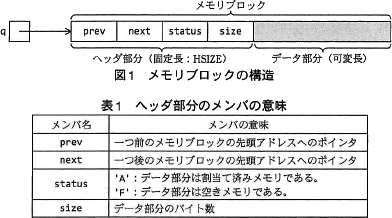 ヘッダー部分と同じ構造体の変数 EDGE をヒープ領域の外に定義する。そのメンバー prev 及び next には,それぞれヒープ領域の最後尾及び先頭のメモリブロックの先頭アドレスをセットする。ヒープ領域の先頭のメモリブロックのメンバー prev と最後尾のメモリブロックのメンバー next には,ともに EDGE の先頭アドレスをセットする。これによって,EDGE を含むメモリブロックが双方向の循環リストを構成する。 EDGE にはデータ部分はなく,メンバー size には 0 が設定されている。データ構造の全体像を図2に示す。
ヘッダー部分と同じ構造体の変数 EDGE をヒープ領域の外に定義する。そのメンバー prev 及び next には,それぞれヒープ領域の最後尾及び先頭のメモリブロックの先頭アドレスをセットする。ヒープ領域の先頭のメモリブロックのメンバー prev と最後尾のメモリブロックのメンバー next には,ともに EDGE の先頭アドレスをセットする。これによって,EDGE を含むメモリブロックが双方向の循環リストを構成する。 EDGE にはデータ部分はなく,メンバー size には 0 が設定されている。データ構造の全体像を図2に示す。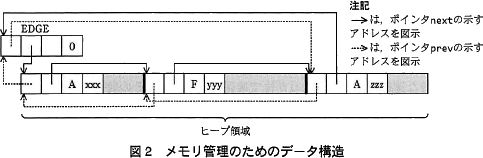 〔メモリ割当ての関数〕
〔メモリ割当ての関数〕
メモリ割当ての関数は,割り当てたいバイト数(msize)を引数とし,そのバイト数以上の大きさのデータ部分をもつメモリブロックを,ヒープ領域から探索する。このアルゴリズムを次のように考えた。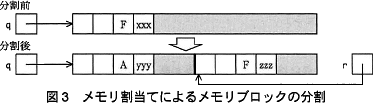 〔メモリ解放の関数〕
〔メモリ解放の関数〕
メモリ解放の関数 freemem は,解放したいメモリブロックの先頭アドレスを引数とし,そのメモリブロックを空きメモリブロックの状態に変更する。このとき,できるだけ大きな連続した空きメモリが後で確保できるよう,その前後のメモリブロックも空きメモリブロックかどうかを確認する。空きメモリブロックが連続する場合には,それらをまとめて一つの空きメモリブロックにする。
関数 freemem のプログラムを図4に示す。この関数を正しく動作させるためには,変数 EDGE のメンバー status の値はカである必要がある。 〔メモリコンパクション〕
〔メモリコンパクション〕
メモリの確保や解放の処理を繰り返すと,サイズの小さな空きメモリが分散してしまい,サイズの大きな空きメモリの確保が難しくなることがある。このような現象をコと呼ぶ。このとき,割当て済みのメモリブロックが連続するようにメモリブロックを移動し,移動したメモリブロックの後ろに大きな空きメモリを確保することをメモリコンパクションという(図5参照)。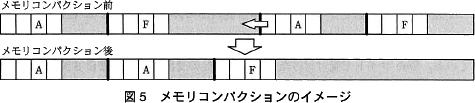 ヒープ領域が図6のように左上から右下にかけて連続する構成の場合,メモリコンパクションを実行すると,サバイトの空きメモリができる。
ヒープ領域が図6のように左上から右下にかけて連続する構成の場合,メモリコンパクションを実行すると,サバイトの空きメモリができる。
メモリコンパクションを実行すると,①メモリコンパクション前に実行したメモリ割当て関数の戻り値は,メモリ解放の関数の引数としては使えなくなる場合がある。
ヒープ領域は,一つ以上の連続したメモリブロックで構成する。メモリブロックは,固定長のヘッダー部分と可変長のデータ部分で構成される。ヘッダー部分は構造体で,prev,next,status 及び size のメンバーによって構成される。メモリブロックの構造を図1に,ヘッダー部分のメンバーの意味を表1にそれぞれ示す。メモリブロックを指すポインタ変数には,メモリブロックの先頭アドレスをセットする。あるメモリブロックを指すポインタ変数を q とするとき,そのメンバー prev の参照は,q->prevと表記する。また,ヘッダー部分のバイト数は,HSIZE とする。


メモリ割当ての関数は,割り当てたいバイト数(msize)を引数とし,そのバイト数以上の大きさのデータ部分をもつメモリブロックを,ヒープ領域から探索する。このアルゴリズムを次のように考えた。
- ポインタ変数 q を定義し,初期値として変数 EDGE の next の値をセットする。
- q がアと等しい場合は,ヒープ領域には十分な空きメモリをもったメモリブロックが無かったことを意味する。関数の戻り値に NULL をセットして終了する。それ以外の場合は,次の(3)~(5)を実行する。
- q->イが'A'の場合,又は q->size が msize 未満である場合は,q に q->ウをセットして(2)に戻る。
- q->size が HSIZE+msize 以下の場合は,q->イに'A'をセットし,関数の戻り値に q の値をセットして終了する。
- q->size が HSIZE+msize よりも大きい場合は,そのメモリブロックを割当て済みのメモリブロックと,残りの空きメモリブロックの二つに分割する(図3参照)。ポインタ変数 r を定義し,初期値として q+HSIZE+msize をセットする。q->イに'A'をセットし,r->イに'F'をセットする。r->size に q->size-HSIZE-msize をセットし,q->size に msize をセットする。r->prev にはエを,r->next にはオを,q->next->prev には r を,q->next には r を順にセットする。関数の戻り値に q の値をセットして終了する。

メモリ解放の関数 freemem は,解放したいメモリブロックの先頭アドレスを引数とし,そのメモリブロックを空きメモリブロックの状態に変更する。このとき,できるだけ大きな連続した空きメモリが後で確保できるよう,その前後のメモリブロックも空きメモリブロックかどうかを確認する。空きメモリブロックが連続する場合には,それらをまとめて一つの空きメモリブロックにする。
関数 freemem のプログラムを図4に示す。この関数を正しく動作させるためには,変数 EDGE のメンバー status の値はカである必要がある。

メモリの確保や解放の処理を繰り返すと,サイズの小さな空きメモリが分散してしまい,サイズの大きな空きメモリの確保が難しくなることがある。このような現象をコと呼ぶ。このとき,割当て済みのメモリブロックが連続するようにメモリブロックを移動し,移動したメモリブロックの後ろに大きな空きメモリを確保することをメモリコンパクションという(図5参照)。

メモリコンパクションを実行すると,①メモリコンパクション前に実行したメモリ割当て関数の戻り値は,メモリ解放の関数の引数としては使えなくなる場合がある。

広告
設問1
〔メモリ割当ての関数〕について,(1),(2)に答えよ。
- 本文中のア~ウに入れる適切な字句を答えよ。
- 本文中のエ,オに入れる適切な字句を,ポインタ変数qを用いて答えよ。
解答例・解答の要点
- ア:EDGEの先頭アドレス
イ:status
ウ:next
- エ:q
オ:q->next
解説
- 先に[イ]と[ウ]に入る字句を考えてから、[ア]に進むとスムーズです。
〔イについて〕
表1「ヘッダー部分のメンバーの意味」よを見ると'A'と'F'の定数を値として持つメンバーは status のみです。よって、[イ]には「status」が入ります。
∴イ=status
〔ウについて〕
q->statusが'A'の場合、すなわち「データ部分は割当て済みメモリである場合」や、q->sizeがmsize未満である場合、すなわち「データ部分のバイト数が割り当てたいバイト数未満」であれば、現在参照しているメモリブロックにメモリを割り当てることはできません。このとき、1つ後のメモリブロックの確認に移るために、q を1つ後のメモリブロックの先頭アドレスで更新することになります。そのメモリブロックの1つ後のメモリブロックの先頭アドレスは、メンバー next が保持しているので、q に q->next を設定する手続きが適切です。
∴ウ=next
〔アについて〕
ポインタ変数 q の初期値は、変数EDGEのメンバー next(リストの先頭要素)です。前述の通り q が割当てできないメモリブロックである場合には、q は1つ後ろのメモリブロックに移動しますが、割当て可能なメモリブロックが見つかったときは関数の戻り値に q をセットして関数を終了します(〔メモリ割当ての関数〕(4)(5)参照)。ここで、もし末尾のメモリブロックまで適切な空きメモリが見つからず、q に末尾のメモリブロックのメンバー next がセットされたとき、q の値はどうなっているのかを考えます。
問題文では「最後尾のメモリブロックのメンバー next には,… EDGEの先頭アドレスをセットする」と説明されているので、末尾のメモリブロックまで走査した結果、十分な空きメモリをもったメモリブロックがなかった場合、q にはEDGEの先頭アドレスがセットされていることになります。よって、q が「EDGEの先頭アドレス」と等しい場合には、関数の戻り値に NULL をセットして終了することになります。
∴ア=EDGEの先頭アドレス - 〔メモリ割当ての関数〕(5)の処理は、q をメモリ割当て済みのメモリブロックと、空きメモリブロック r に分割する処理です。
図3「メモリ割り当てによるメモリ分割」より、空きメモリブロック r は q の1つ後ろのメモリブロックになることがわかります。したがって、リスト内のメモリブロックの連結が以下のように変わることになります。- 分割前
- qの1つ前のブロック ←→ q ←→ qの1つ前のブロック
- 分割後
- qの1つ前のブロック ←→ q ←→ r ←→ qの1つ前のブロック
r->prev は、r の1つ前のメモリブロックの先頭アドレスなので、「q」をセットするのが適切です。
〔オについて〕
r->next は、r の1つ後のメモリブロックの先頭アドレスなので、「q->next」をセットするのが適切です。q->next の値を r に更新する処理は最後に行っているので、q->next で分割前の q の1つ後ろのメモリブロックを参照可能です。
∴エ=q
オ=q->next
広告
設問2
〔メモリ解放の関数〕について,(1),(2)に答えよ。
- 本文中のカに入れる適切な字句を答えよ。
- 図4中のキ~ケに入れる適切な字句を答えよ。
解答例・解答の要点
- カ:'A'
- キ:p->size + q->size + r->size + 2*HSIZE
ク:p
ケ:q->size + r->size + HSIZE
解説
- 〔カについて〕
status に設定する値ですので、'A'または'F'の択一です。
関数 freemem 中では、前後のブロックの少なくとも1つが空きブロックである場合には、それらをまとめて1つの空きブロックにします。この際、空きブロックのメンバー size を設定していますが、変数 EDGE はデータ部分を持っていない(size=0)ので、p や r となったときに空きブロックとして扱われてしまうのは適切ではありません。特に p になったときは、変数EDGEのメンバー size を空きブロックのデータサイズで更新してしまうことになります。
よって、変数EDGEのメンバー status には'A'(割当て済)をセットしておき、空きブロックとして扱われないようにしておく必要があります。
∴カ='A' - 〔キについて〕
コメント部にあるように、この分岐は前後のブロックがともに空きであるときの処理です。この場合、前・解放対象・後の3つのブロックの空き領域を前のブロック(p)にまとめることになります。解放対象のブロック及び後のブロックについては、解放によりヘッダー部分とデータ部分の両方が空き領域となるので、前のブロックのメンバー size に設定する値は以下の3つの合計となります。
- 前のブロックのデータサイズ
- 解放対象のブロックのヘッダーサイズ+データサイズ
- 後のブロックのヘッダーサイズ+データサイズ
したがって p->size に設定する値は、p->size、q->size、r->size とヘッダー部分のバイト数である HSIZE 2つ分(HSIZE * 2)の合計となります。
∴キ=p->size + q->size + r->size + 2*HSIZE
〔クについて〕
空き領域を前のメモリブロックにまとめると、まとめられた側のメモリブロック(qやr)は不要となるのでリストから外されます。このとき、リストの連結を維持するために前のメモリブロック(p)のメンバー next を更新する必要があります。具体的には、p->next の値は関数 freemem の6行目または9行目で次の値で更新されています。- 前後とも空きの場合(6行目)
- p ←→ q ←→ r ←→ rの1つ後
が
p ←→ rの1つ後
となるので、r->next を設定 - 前だけが空きの場合(9行目)
- p ←→ q ←→ r
が
p ←→ r
となるので、r を設定
∴ク=p
〔ケについて〕
コメント部にあるように、この分岐は前が割当て済で、後が空きであるときの処理です。この場合、解放対象・後の2つのブロックの空き領域を解放対象のブロック(q)にまとめることになります。後のブロックについては、解放によりヘッダー部分とデータ部分の両方が空き領域となるので、解放対象のブロックのメンバー size に設定する値は以下の2つの合計となります。
- 解放対象のブロックのデータサイズ
- 後のブロックのヘッダーサイズ+データサイズ
したがって q->size に設定する値は、q->size、r->size とヘッダー部分のバイト数である HSIZE 1つ分の合計となります。
∴ケ=q->size + r->size + HSIZE
広告
設問3
〔メモリコンパクション〕について,(1)~(3)に答えよ。
- 本文中のコに入れる適切な字句をカタカナで答えよ。
- 本文中のサに入れる適切な式を答えよ。
- 本文中の下線①の理由を25字以内で述べよ。
解答例・解答の要点
- コ:フラグメンテーション
- サ:2×HSIZE+600
- メモリブロックの先頭アドレスが変わるから (20文字)
解説
- 記憶領域を区画してプログラムに割り当てていくと、その結果として記憶領域上に小さな空き領域が点在した状態になります。この状態になると空き領域の合計としては余裕があるにもかかわらず、サイズの大きな空きメモリの確保が難しくなり、アクセス効率が低下します。この現象を「フラグメンテーション」と呼びます。
∴コ=フラグメンテーション - 〔サについて〕
図6「ヒープ領域の状態」を見ると、割当て済(status='A')のメモリが4つ、空きメモリ(status='F')が3つあります。この3つの空メモリの size を合計すると「200+300+100=600」となります。メモリコンパクションを行うと複数の空きメモリが1つの大きな空きメモリにまとまるので、ヘッダー部分が1つで済みます。3つの空きメモリを1つの空きメモリにまとめた場合、2つのヘッダー部分の領域もデータ部分として使用できることになります。
したがって、図6の状態にメモリコンパクションを実行した場合にできる空きメモリの大きさは、600バイトに HSIZE 2つ分を足した「2×HSIZE+600」が適切です。
∴サ=2×HSIZE+600 - メモリ割当ての関数の戻り値である q は、割当て可能とされたメモリブロックの先頭アドレスです。メモリコンパクションでは、割当て済みのメモリブロックが連続するようにメモリブロックを移動するので、移動対象となった割当て済みメモリについては先頭アドレスが変わることになります。このため、メモリ解放の関数の引数として戻り値の q を指定しても、正しく参照できないことがあります。
∴メモリブロックの先頭アドレスが変わるから
広告
広告