平成25年春期試験問題 午前問7
広告
解説
指定された整数に対して、その数以下のすべての素数を抽出する方法の中で最も単純なものに「エラトステネスの篩」があります。この方法では、
設問のアルゴリズムは「エラトステネスの篩」をプログラムで実装したものです。このプログラムは次の3つのブロックで構成されています。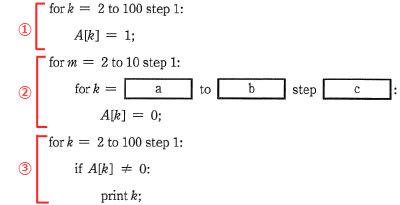 処理中の②では、0に書き換えられる要素の配列の添え字が素数となるように二重のループを制御する必要があります。②の、
処理中の②では、0に書き換えられる要素の配列の添え字が素数となるように二重のループを制御する必要があります。②の、
- 最初の素数である"2"から昇順に整列された探索リストを用意する
- 探索リストから、2を除く2の倍数を取り除く
- 探索リストから、3を除く3の倍数を取り除く
- 続く4は、2の倍数の処理にて探索リストから取り除かれているので次の数へ
- 以降、探索リスト内に残っている最大値が、現在の倍数の元となる数の2乗以下になるまで同様の処理を繰り返す。(探索リストの最大値が100であれば10の倍数を取り除くまで繰り返す)
設問のアルゴリズムは「エラトステネスの篩」をプログラムで実装したものです。このプログラムは次の3つのブロックで構成されています。
- 配列A[2]~配列A[100]の99個の要素を1で初期化する。
- 配列中の添え字が素数ではない要素に0を設定する。
- 配列中の値が1である要素の添え字を出力する。

for m=2 to 10 step 1:
は、処理対象である2≦k≦100に応じて、mを2から(100の平方根である)10まで増やして処理を行うためのループ文です。続くa、b、cが含まれるfor k=a to b step c:
A[k]=0;
の部分は「エラトステネスの篩」における「mでないmの倍数を探索リストから除外する」処理に相当します。これをm=2の場合で考えてみると、kに対して4,6,8,10,12,…,100という順番で値が格納されていけば、配列の添え字が素数でないA[k]には0が格納される(素数でないと判定される)ことになります。m=2であれば、初期値は4、終値は100,増分は2、同様にm=3であれば、6,9,12,15,…,99を除外するので初期値は6、終値は100、増分は3です。これらの値からループ変数を逆算的に導くと、ループ変数kに素数でない数を格納させるためには、初期値(a)に2m、終値(b)に100、増分(c)にmを指定するのが適切とわかります。A[k]=0;
広告