平成26年春期試験午後問題 問3
問3 プログラミング
⇱問題PDF
循環小数の循環節を検出するアルゴリズムに関する次の記述を読んで,設問1~4に答えよ。
循環小数の循環節を検出するアルゴリズムに関する次の記述を読んで,設問1~4に答えよ。
広告
与えられた自然数 n について,1/n の小数表現を考える。1/n は,割り切れない場合,必ず循環小数となる。本問において,循環小数は,図1に示すように,繰り返し現れる数の並びである循環節の先頭から末尾までを括弧でくくる表記法で表す。
1 を n で割る割り算で現れる余りは,1 から n-1 までの値に限られる。循環小数となる場合は,割り算を小数第1位から行っていくと,どこかでそれまでに現れた余りと同じ値の余りが現れる。以降の割り算で得られる小数は,同じ数の並びが繰り返されることとなり,その数の並びが循環節となる。循環節の桁数は最大 n-1 である。 1/56の計算で商を1桁ずつ求めていくと,余りの選移は図2のようになる。ここでは,前のマスの中の値を10倍して 56 で割った余りが次のマスの中の値となる。余りとして 48 が再度現れることから,1/56では小数第4位から第9位までが循環節となることが分かる。
1/56の計算で商を1桁ずつ求めていくと,余りの選移は図2のようになる。ここでは,前のマスの中の値を10倍して 56 で割った余りが次のマスの中の値となる。余りとして 48 が再度現れることから,1/56では小数第4位から第9位までが循環節となることが分かる。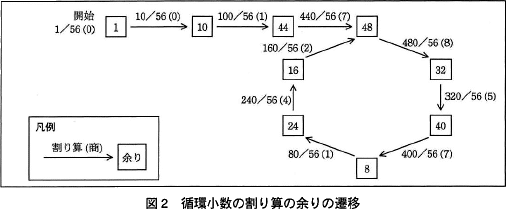 〔循環節を検出するアルゴリズム〕
〔循環節を検出するアルゴリズム〕
単純に余りを配列に記録して,既出の余りであるかどうか比較することによって循環節を検出する方法では,割り算の各桁で現れる余りの種類の最大である n-1 種類の余りを記録する必要がある。その配列の大きさは n に比例することになり,処理できる n の値は使用可能な記憶域の大きさによって制約される。そこで記憶域の制約を受けない,"ウサギとカメ"に例えられるフロイドの循環検出法のアルゴリズムを用いる。この検出法は,循環するデータの先頭と末尾の位置を効率よく検出できることが証明されている。
図2の余りを格納したマスから次のマスへ割り算を1桁進めることを,"ウサギとカメ"の歩みに例えて1歩進むという。このアルゴリズムでは,まず,図3に示すように,カメは〈1〉,〈2〉,…と一度に1歩ずつ,ウサギは《1》,《2》,…と一度に2歩ずつ進む。両者は同時に出発し,進んだマス(〈1〉と《1》,〈2〉と《2》,…)の余りを比較しながら,余りが一致するところ(〈6〉と《6》)まで進む。
このように,循環小数となる全ての n において,ウサギは循環部分の何巡目かで周回遅れのカメに必ず追い付き,両者の余りは一致する。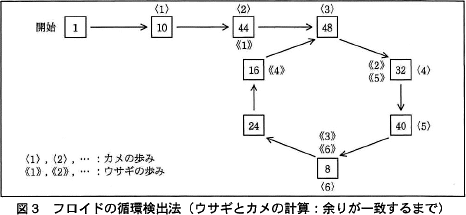 両者の余りが一致したら,図4に示すように,カメは引き続き,ウサギは最初に戻って今度は両者とも1歩ずつ進む。最初に両者の余りが一致したところ(〈9〉と《9》)の次の割り算の商が,循環節の先頭である。
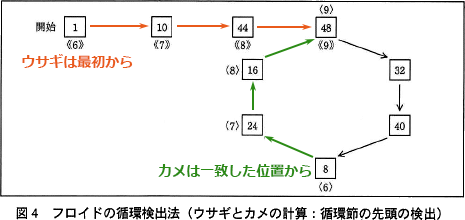
両者の余りが一致したら,図4に示すように,カメは引き続き,ウサギは最初に戻って今度は両者とも1歩ずつ進む。最初に両者の余りが一致したところ(〈9〉と《9》)の次の割り算の商が,循環節の先頭である。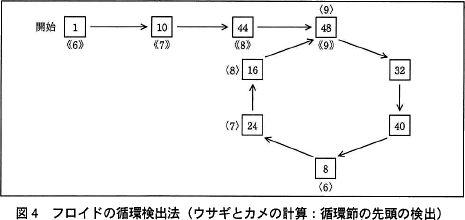 循環節の先頭を検出した後,図5に示すように,ウサギだけが再びカメと余りが一致するところ(〈9〉と《15》)まで1歩ずつ進むことによって,循環節の末尾を検出する。
循環節の先頭を検出した後,図5に示すように,ウサギだけが再びカメと余りが一致するところ(〈9〉と《15》)まで1歩ずつ進むことによって,循環節の末尾を検出する。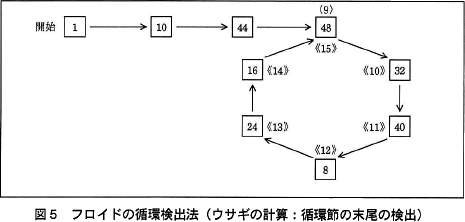 このアルゴリズムを使って循環節の先頭と末尾の桁位置を求める関数 junkan を図6に示す。図6で使用する変数と関数は,表1のとおりである。
このアルゴリズムを使って循環節の先頭と末尾の桁位置を求める関数 junkan を図6に示す。図6で使用する変数と関数は,表1のとおりである。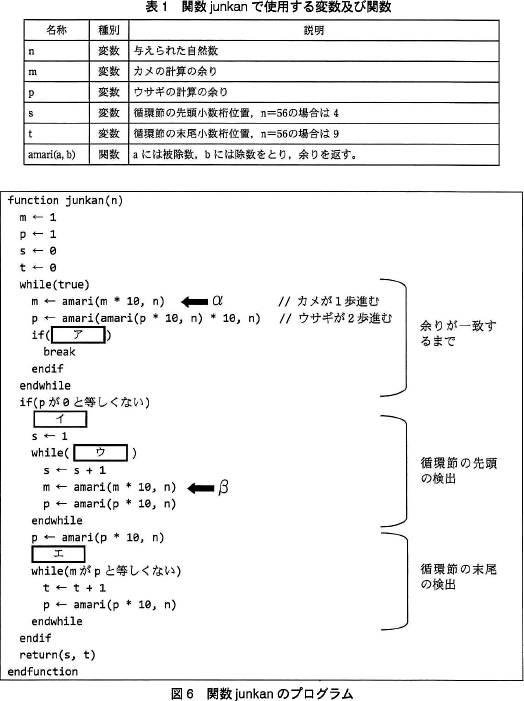 与えられた n に基づき,O記法で表した場合,関数 junkan のプログラムが必要とする記憶域の大きさはオとなり,計算量はカとなる。
与えられた n に基づき,O記法で表した場合,関数 junkan のプログラムが必要とする記憶域の大きさはオとなり,計算量はカとなる。
1 を n で割る割り算で現れる余りは,1 から n-1 までの値に限られる。循環小数となる場合は,割り算を小数第1位から行っていくと,どこかでそれまでに現れた余りと同じ値の余りが現れる。以降の割り算で得られる小数は,同じ数の並びが繰り返されることとなり,その数の並びが循環節となる。循環節の桁数は最大 n-1 である。


単純に余りを配列に記録して,既出の余りであるかどうか比較することによって循環節を検出する方法では,割り算の各桁で現れる余りの種類の最大である n-1 種類の余りを記録する必要がある。その配列の大きさは n に比例することになり,処理できる n の値は使用可能な記憶域の大きさによって制約される。そこで記憶域の制約を受けない,"ウサギとカメ"に例えられるフロイドの循環検出法のアルゴリズムを用いる。この検出法は,循環するデータの先頭と末尾の位置を効率よく検出できることが証明されている。
図2の余りを格納したマスから次のマスへ割り算を1桁進めることを,"ウサギとカメ"の歩みに例えて1歩進むという。このアルゴリズムでは,まず,図3に示すように,カメは〈1〉,〈2〉,…と一度に1歩ずつ,ウサギは《1》,《2》,…と一度に2歩ずつ進む。両者は同時に出発し,進んだマス(〈1〉と《1》,〈2〉と《2》,…)の余りを比較しながら,余りが一致するところ(〈6〉と《6》)まで進む。
このように,循環小数となる全ての n において,ウサギは循環部分の何巡目かで周回遅れのカメに必ず追い付き,両者の余りは一致する。




広告
設問1
図6中のア~エに入れる適切な字句を答えよ。
解答例・解答の要点
ア:mがpと等しい
イ:p ← 1
ウ:mがpと等しくない
エ:t ← s
イ:p ← 1
ウ:mがpと等しくない
エ:t ← s
解説
〔アについて〕whileループの継続条件が true になっているので、ループ終了の際にはbreak文を使って明示的に抜ける必要があります。if文では[ア]が真のときにbreak文が実行されるため、[ア]にはwhileループの終了条件が入ることがわかります。
〔関数 junkan のプログラム〕の最初のwhileループ処理は、図3で示されている「余りが一致するまで」の処理に該当します。また、当該whileループ処理のコメント部には、「余りが一致するまで」と書かれています。図6の7行目から8行目の処理と、表1「関数junkanで使用する変数及び関数」より、変数 m にカメの計算の余りを、変数 p にウサギの計算の余りを格納していることがわかります。循環検出法の第1フェーズは両者が一致したときに終了となるので、[ア]には「mとpが等しい」が入ります。
∴ア=mとpが等しい
〔イについて〕
プログラムの14行目から20行目までは、図4で示されている「循環節の先頭の検出」の処理に該当します。このフェーズでは「カメは引き続き,ウサギは最初に戻って今度は両者とも1歩ずつ進む」と説明されています。
∴イ=p ← 1
〔ウについて〕
[ウ]も[イ]と同様に、図4「循環節の先頭の検出」の処理に該当します。この処理については、本文中に「最初に両者の余りが一致したところ(〈9〉と《9》)の次の割り算の商が、循環節の先頭である」とあります。このことから、カメの計算の余り(変数m)とウサギの計算の余り(変数p)が一致するまで、それぞれを一歩ずつ進める処理を繰り返すことがわかります。[ウ]にはループの継続条件が入りますから、余りが一致しない間繰返しを行う「mがpと等しくない」という条件が適切となります。
ウサギとカメが1歩進むごとに s(循環節の先頭位置)も1ずつ増えるので、図4のようにそれぞれ3歩進んで余りが一致したとき、s は4になっています。
∴ウ=mがpと等しくない
〔エについて〕
図6中の21行目から26行目までは、図5で示されている「循環節の末尾の検出」の処理に該当します。この処理については、本文中に「循環節の先頭を検出した後、図5に示すように、ウサギだけが再びカメと余りが一致するところ(〈9〉と《15》)まで1歩ずつ進むことによって、循環節の末尾を検出する」とあります。whileループ内では、ウサギが1歩進むたびに変数 t を1増加させていますが、図5を見るとわかるように、変数 t は0からではなく循環節の先頭を基準に1ずつ増加させる必要があります。変数 t はプログラムの冒頭で0に初期化されたままなので、ここには循環節の先頭が格納されている変数 s を使って変数 t に基準位置を設定する処理が入ることが予想できます。
ここで、例示されている n=56 の末尾検出処理を考えてみます。
第2フェーズで循環節の先頭位置4を変数 s に求めた後、[エ]の直前で amari() を1回を実行してウサギの位置を一歩進めているので、whileループ開始時の変数 p は一致位置の次の位置(余り32)になっています。そこから余りが一致するまでウサギを進めると t には5が加算されることになります。
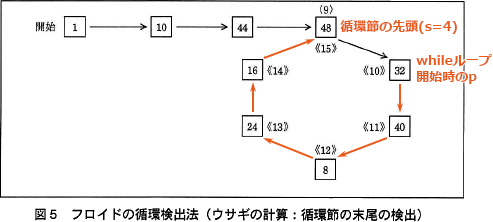
∴エ=t ← s
広告
設問2
n=88のとき,図6中のαとβはそれぞれ何回実行されるか答えよ。
解答例・解答の要点
α:4
β:3
β:3
解説
〔αについて〕図6「関数junkanのプログラム」の6行目から12行目までのループ回数と、変数 m および変数 p の値の遷移を考えます。
図6の2行目と3行目から、m=1、p=1 が初期値であることがわかります。その後、次のように処理されていきます。
- ループ1回目
- m = 1×10÷88の余り = 10
p = (1×10÷88の余り)×10÷88の余り = 12 - ループ2回目
- m = 10×10÷88の余り = 12
p = (12×10÷88の余り)×10÷88の余り = 56 - ループ3回目
- m = 12×10÷88の余り = 32
p = (56×10÷88の余り)×10÷88の余り = 56 - ループ4回目
- m = 32×10÷88の余り = 56
p = (56×10÷88の余り)×10÷88の余り = 56
∴α=4
〔βについて〕
図6「関数junkanのプログラム」の13行目から20行目までのループ回数と、変数 s、変数 m および変数 p の値の遷移を考えます。
前述のように、プログラム中の「余りが一致するまで」が終了した時点で、m=56、p=56 になっています。 その後、次のように処理されていきます。
- p ← 1
- s=0、m=56、p=1
- s ← 1
- s=1、m=56、p=1
- ループ1回目
- s = s+1 = 1+1 = 2
m = m×10÷88の余り = 56×10÷88の余り = 32
p = p×10÷88の余り = 1×10÷88の余り = 10 - ループ2回目
- s = s+1 = 2+1 = 3
m = m×10÷88の余り = 32×10÷88の余り = 56
p = p×10÷88の余り = 10×10÷88の余り = 12 - ループ3回目
- s = s+1 = 3+1 = 4
m = m×10÷88の余り = 56×10÷88の余り = 32
p = p×10÷88の余り = 12×10÷88の余り = 32
∴β=3
広告
設問3
1/nが割り切れるとき,関数 junkan の戻り値はどのようになるか。15字以内で述べよ。
解答例・解答の要点
s,tともに0である (10文字)
解説
1/nが割り切れる場合は循環節が存在しません。このため循環節の先頭が検出されることはなく、割り切れた時点で m 及び p の値は0に帰着します。その後、p が m に追いつき、余り0(m=0,p=0)で一致してループが終了することになります。この場合、プログラム13行目の条件式「pが0と等しくない」を満たさないため、14行目から27行目までの処理は行わずに、28行目の「return(s, t)」が実行されます。変数 s と変数 t は初期値である0から更新されていないため、関数 junkan は s、t ともに0を返します。
∴s、tともに0である
広告
設問4
本文中のオ~カに入れる適切な字句を答えよ。
解答例・解答の要点
オ:O(1)
カ:O(n)
カ:O(n)
解説
O(オーダー)記法は、実行時に処理するデータ量によってアルゴリズムの計算量がどの程度増加するか、という視点でアルゴリズムを評価するものです。[オ]は空間計算量、[カ]では時間計算量について問われています。- 空間計算量
- 処理を達成するために必要な記憶領域の大きさ
- 時間計算量
- 処理を達成するために必要な時間
〔オについて〕
関数 junkan のプログラムが必要とする記憶領域の大きさを考えます。
必要とする記憶領域の大きさは、関数内で宣言する変数の数に依存します。
表1「関数junkanで使用する変数及び関数」より、関数junkanのプログラムでは、5つの変数を使用していることがわかります。変数の数は定数であり、与えられたnによらず一定です。計算量がデータ量に依存しない場合、O記法では「O(1)」と表します。
∴オ=O(1)
〔カについて〕
関数 junkan のプログラムの計算量を考えます。
関数 junkan のプログラムは、「余りが一致するまで」「循環節の先頭の検出」「循環節の末尾の検出」の3つの繰返し処理で構成されています。循環節の桁数が最大 n-1 であることから、3つの処理のいずれも最大 n-1 回で計算可能です。計算量がデータ量nに比例する場合、O記法では「O(n)」と表します。
∴カ=O(n)
広告

広告