平成28年春期試験午後問題 問3
問3 プログラミング
⇱問題PDF
ライフゲームに関する次の記述を読んで,設問1~5に答えよ。
ライフゲームに関する次の記述を読んで,設問1~5に答えよ。
広告
ライフゲームとは,数学者コンウェイが考案した,生命の誕生,生存,死滅などを再現したシミュレーションゲームである。マス目状の盤上の各マスに生命が存在でき,そのマス自身及び隣接するマスの状態によって次世代の誕生,生存,死滅が決まる。その条件を表1に示す。
なお,隣接するマスには,斜め方向のマスも含む。また,生命が存在するマスを"生のマス",生命が存在しないマスを"死のマス"と呼ぶ。 〔4×4マスのシミュレーション〕
〔4×4マスのシミュレーション〕
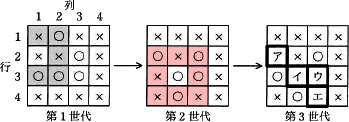
4×4マスの盤上における第3世代までのシミュレーションを図1に示す。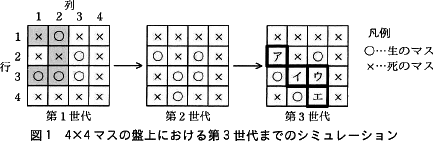 第1世代は,初期値として設定されたものである。例として,第1世代の2行目1列目のマスを考える。現在,このマスは死のマスである。このマスに隣接するマスを網掛けで示す。これら五つのマスの中に生のマスが三つある。これは表1の"誕生"の条件に該当するので,第2世代の2行目1列目のマスは生のマスになる。同様に,第1世代の各マスについて,そのマス自身及び隣接するマスの状態を確認することで第2世代が決まる。次の世代への状態の更新は,全てのマスについて同時に行われる。
第1世代は,初期値として設定されたものである。例として,第1世代の2行目1列目のマスを考える。現在,このマスは死のマスである。このマスに隣接するマスを網掛けで示す。これら五つのマスの中に生のマスが三つある。これは表1の"誕生"の条件に該当するので,第2世代の2行目1列目のマスは生のマスになる。同様に,第1世代の各マスについて,そのマス自身及び隣接するマスの状態を確認することで第2世代が決まる。次の世代への状態の更新は,全てのマスについて同時に行われる。
〔盤上のマスのデータ構造〕
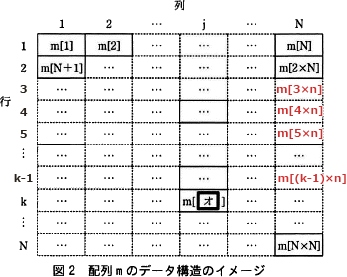
N×Nマスの盤上の状態を表現するデータ構造を考える。多次元配列が利用できないプログラム言語を考慮し,盤上の各マスの生死状態を管理するデータ構造として1次元配列mを用いる。配列mのデータ構造のイメージを図2に示す。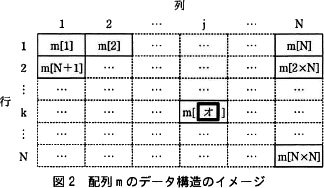 〔配列mを次世代に更新するプログラム〕
〔配列mを次世代に更新するプログラム〕
使用する定数,配列及び関数を表2に,配列mを次世代に更新する関数 update を図3に示す。
なお,関数に配列を引数として渡すときの方式は参照渡しである。 〔テストプログラム〕
〔テストプログラム〕
図3のプログラムをテストするために,配列mに第1世代が与えられたときの第p世代が,机上で作成した正しい結果である配列rと等しいことを確認するプログラムを作成した。作成した関数 shouldBe を図4に示す。ここで,pには2以上の整数が入る。 図3のプログラムが正しく動作する状態で図4のプログラムを実行したところ,テストが失敗した。原因を調査した結果,図4のケ行目に問題があることが判明したので,①プログラムを修正してテストを成功させることができた。
図3のプログラムが正しく動作する状態で図4のプログラムを実行したところ,テストが失敗した。原因を調査した結果,図4のケ行目に問題があることが判明したので,①プログラムを修正してテストを成功させることができた。
なお,隣接するマスには,斜め方向のマスも含む。また,生命が存在するマスを"生のマス",生命が存在しないマスを"死のマス"と呼ぶ。

4×4マスの盤上における第3世代までのシミュレーションを図1に示す。

〔盤上のマスのデータ構造〕
N×Nマスの盤上の状態を表現するデータ構造を考える。多次元配列が利用できないプログラム言語を考慮し,盤上の各マスの生死状態を管理するデータ構造として1次元配列mを用いる。配列mのデータ構造のイメージを図2に示す。

使用する定数,配列及び関数を表2に,配列mを次世代に更新する関数 update を図3に示す。
なお,関数に配列を引数として渡すときの方式は参照渡しである。

図3のプログラムをテストするために,配列mに第1世代が与えられたときの第p世代が,机上で作成した正しい結果である配列rと等しいことを確認するプログラムを作成した。作成した関数 shouldBe を図4に示す。ここで,pには2以上の整数が入る。

広告
設問1
図1中のア~エに入れる適切な生死状態を,図1の凡例に倣い答えよ。
解答例・解答の要点
ア:×
イ:×
ウ:○
エ:○
イ:×
ウ:○
エ:○
解説
誕生、生存、死滅は現在のマスの状態と隣接する生のマスの数によって決定されます。ライフゲームの条件を決定木として整理したものが下図です。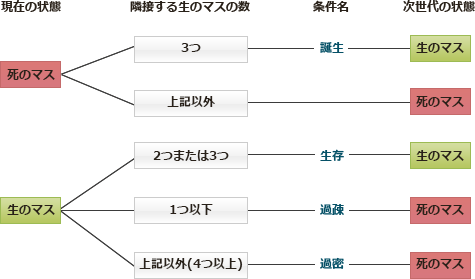
図1の第2世代を見ると[ア]は生のマスであり、隣接する生のマスは1つ、死のマスは4つであることがわかります。
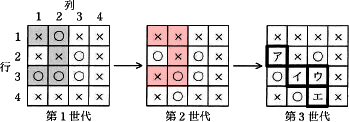
〔イについて〕
図1の第2世代を見ると[イ]は生のマスであり、隣接する生のマスは4つ、死のマスは4つであることがわかります。
〔ウについて〕
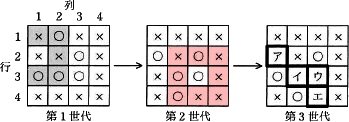
第2世代の[ウ]は生のマスであり、隣接する生のマスは3つ、死のマスは5つです。
〔エについて〕
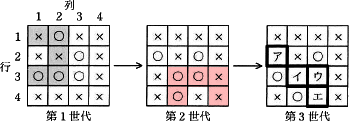
第2世代の[エ]は死のマスであり、隣接する生のマスは3つ、死のマスは3つです。
∴ア=×
イ=×
ウ=○
エ=○
広告
設問2
図2中のオに入れる適切な字句を答えよ。
解答例・解答の要点
オ:(k-1)×N+j
解説
〔オについて〕図2を参考に空欄に入る字句を考えます。
まず、図2の3行目N列目について考えます。2行目N列目が m[2×N] であり、そこからNだけ進んだ場所になるので、3行目N列目は m[3×N] であることがわかります。同様に、4行目N列目は m[4×N]、5行目1列目は m[5×N] …となります。すなわち、kの1つ前の行である(k-1)行目N列目は m[(k-1)×N] と表すことができます。よって配列の添字は になります。

広告
設問3
図3中のカ~クに入れる適切な字句を答えよ。
解答例・解答の要点
カ:temp[c]と1が等しい
キ:(temp[i]と0が等しい) and (eと3が等しい)
ク:m[i]←1
キ:(temp[i]と0が等しい) and (eと3が等しい)
ク:m[i]←1
解説
〔カについて〕図3のプログラムは、配列mを次世代にupdateする関数です。
17~29行目は、m[i]のマスに隣接する生のマスの数を求める処理です。プログラム中の変数cは隣接するマスの添字を表します。また、変数eは隣接する生のマスの数を表します。
[カ]の条件を満たすとき、eの値を+1する処理を行っていることから、[カ]に入る条件式は「隣接するマスが生のマスであるとき」であることがわかります。配列mは2行目の処理で初期化されているため、隣接するマスの確認には配列mのコピーである配列tempを使います。配列tempの値は、対応するマスが生の場合は1、死の場合は0ですので、[カ]には「temp[c]と1が等しい」が入ります。
なお、プログラムの最初に配列mを配列tempにコピーしているのは、次世代への状態の更新を現在の状態に基づいて同時に行うためです。
∴カ=temp[c]と1が等しい
〔キについて〕
[キ]と[ク]を含む5行の処理はコメント部に説明されているように、現在参照しているマスの情報から次世代の生死を判定して、その結果を配列mに書き込む処理です。
[キ]の条件を満たすとき、「m[i] ← 1」という処理を行っています。"1"は生のマスを表すので、これは「m[i]のマスの次世代を生にする」処理に相当します。次の世代が生のマスになる条件は次の2つです。
- 前の世代が死のマス、かつ、隣接する生のマスの数が3つである
- 前の世代が生のマス、かつ、隣接する生のマスの数が2つまたは3つである
※プログラム中盤のif文の条件式を参照すると、条件式が複数から成るときには個々の式を()で括ること、及び"かつ"と"または"は、それぞれ"and"と"or"で表現するルールになっていることがわかります。
- (temp[i]が0と等しい) and (eが3と等しい)
- (temp[i]が1と等しい) and ((eが2と等しい) or (eが3と等しい))
∴キ=(temp[i]と0が等しい) and (eと3が等しい)
〔クについて〕
[ク]の処理は、上記①の条件が真であるときに実行されます。つまり、「前の世代が生のマス、かつ、隣接する生のマスの数が2つまたは3つである」ときの処理です。この条件を満たすマスは"生存"に当てはまるため、次の世代は生のマスになります。よって、[ク]には m[i] に"1"を代入する処理が入ります。
∴ク=m[i] ← 1
広告
設問4
図3中のαの二つの条件のいずれかを満たすのはどのような場合か。単語"盤"及び"マス"を用いて30字以内で述べよ。
解答例・解答の要点
チェックするマスが盤の第1列又は第N列の場合 (22文字)
解説
αを含む一連の処理は、aとbの値を調整する処理です。aとbは、その後のfor文でx(列)の開始位置と終了位置を指定する変数です。なぜこのような処理をしなければならないのかというと、チェックするマスの隣接するマスの数と位置が、中心となるマスの位置によって変わるからです。
- 1列目のとき
- 隣接するマスは1列目と2列目なので、a←0、b←1 にする
- N列目のとき
- 隣接するマスはN-1列目とN列目なので、a←-1、b←0 にする
- その他(x列目のとき)
- 隣接するマスはx-1列目、x列目、x+1列目なので、a←-1、b←1 にする
まず、「i-1がNで割り切れる」場合を考えます。仮に N=5 だとすると、i-1 が N で割り切れるときの i は、6、11、16、21、…です。これは i×N+1 の数であり、どれも盤上の1列目に対応します。
次に、「iがNで割り切れる」場合を考えます。先程と同様に N=5 だとすると、i が N で割り切れるときの i は、5、10、15、20、…です。これは i×N の数であり、どれも盤上のN列目に対応します。
よって、αの2つの条件を満たすのは、「チェックするマスが盤の第1列又は第N列の場合」となります。
∴チェックするマスが盤の第1列又は第N列の場合
広告
設問5
〔テストプログラム〕について,(1),(2)に答えよ。
- 本文中のケに入れる適切な数値を答えよ。
- 本文中の下線①の修正後のケ行目のプログラムを答えよ。
解答例・解答の要点
- ケ:2
- for (iを2からpまで1ずつ増やす)
解説
update関数は配列mを次世代に更新する関数です。最初の世代(第1世代)に対してupdate関数を1回実行すると、配列mは第2世代に更新されます。図3のテストプログラムでは、第p世代が正しい結果であることを確認するためのプログラムです。仮に第5世代を検証したい場合、p=5ですので、2行目のfor文内のupdate関数は(i=1…5までの)5回実行されます。第1世代にupdate関数を5回適用すると配列mは第6世代になります。検証したいのは第5世代の配列mですが、図3のプログラムでは第6世代の配列mと第5世代の配列rを比較することになってしまいます。
配列mを第p世代にしたいときには、update関数をp-1回実行しなければなりません。図3のプログラムではp回実行してしまうので、テストは常に失敗します。つまり、誤りがあるのは2行目のfor文の継続条件です。
これを改善するには、update関数がp-1回実行されるようにプログラムを変更する必要があります。for文の「1からpまで」を「2からpまで」若しくは「1から(p-1)まで」に変更することでこの目的を達成できます。模範解答では「2からpまで」の方が採用されていますが、for文内でiが使用されているわけではないため、プログラム的にはどちらでも構わないと思います。
∴(1) ケ=2
(2) for (iを2からpまで1ずつ増やす)
広告

広告