平成30年春期試験午後問題 問3
問3 プログラミング
⇱問題PDF
ナイトの巡歴問題に関する次の記述を読んで,設問1~3に答えよ。
ナイトの巡歴問題に関する次の記述を読んで,設問1~3に答えよ。
広告
ナイトの巡歴問題とは,M行N列(以下,M×Nマスという)の盤面上でチェスの駒の一種であるナイトを移動させ,全てのマスを1回ずつ通過する経路を発見する問題である。
ナイト(K)が1回で移動できるマス(以下,移動先という)の位置を図1に示す。また,4×3マスの場合のナイトの巡歴問題の解の一つを図2に示す。図2に示す,ナイトの移動する順序を表す数を,移動順序という。
なお,行番号は上から下,列番号は左から右に増加する。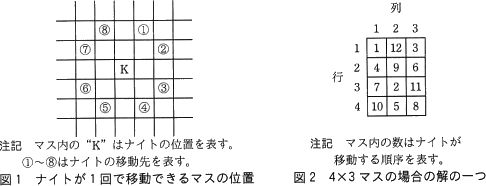 M×Nマスのナイトの巡歴問題について,行1列1のマスを起点とする全ての経路を求める処理の概要を示す。この処理は,再帰による深さ優先探索として実現されている。
M×Nマスのナイトの巡歴問題について,行1列1のマスを起点とする全ての経路を求める処理の概要を示す。この処理は,再帰による深さ優先探索として実現されている。
〔ナイトの巡歴問題の処理の概要〕
(1) 移動順序1,行1,列1で,再帰関数 search を呼び出す。
再帰関数 search(移動順序,行,列)
この処理の概要をプログラムに実装するために,M×Nマスの盤面,ナイトの移動先をそれぞれ次のデータ構造で表現することにした。 〔ナイトの巡歴問題の解法のプログラム〕
〔ナイトの巡歴問題の解法のプログラム〕
M×Nマスのナイトの巡歴問題について,解法のプログラムを考える。
解法のプログラムで使用する定数,変数及び関数を表2に示す。 再帰関数 search のプログラムを図3に,解答を印字する関数 printBoard のプログラムを図4に,メインプログラムを図5に示す。
再帰関数 search のプログラムを図3に,解答を印字する関数 printBoard のプログラムを図4に,メインプログラムを図5に示す。
なお,左側の番号はプログラムの行番号を示す。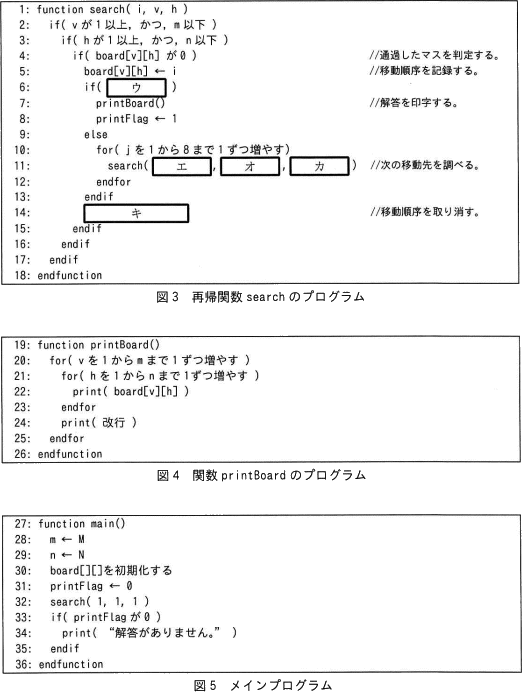 〔盤面の表現の変更〕
〔盤面の表現の変更〕
ナイトの移動先が盤面の範囲外となった場合の判定処理を簡略化するために,図6のように盤面をナイトが移動できるマスが全て含まれる範囲まで拡大して表現する。
この変更に合わせて①関数 printBoard の変更,②メインプログラムの変更,③再帰関数 search の一部の行の削除を同時に行うことによって,プログラムを短縮することができる。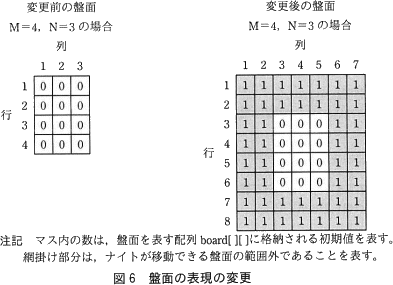
ナイト(K)が1回で移動できるマス(以下,移動先という)の位置を図1に示す。また,4×3マスの場合のナイトの巡歴問題の解の一つを図2に示す。図2に示す,ナイトの移動する順序を表す数を,移動順序という。
なお,行番号は上から下,列番号は左から右に増加する。

〔ナイトの巡歴問題の処理の概要〕
(1) 移動順序1,行1,列1で,再帰関数 search を呼び出す。
再帰関数 search(移動順序,行,列)
- 行と列で指定されるマス(以下,現在のマスという)が盤面の範囲外,又は既に通過したマスであった場合,何もせずに再帰関数 search の呼出し元へ戻る。
- (i)以外の場合,現在のマスに,移動順序を記録する。
- (ⅱ-1)
- 記録した移動順序がM×Nに等しい場合,その経路を解の一つとして出力する。
- (ⅱ-2)
- (ⅱ-1)以外の場合,現在のマスを起点とした図1の移動先①~⑧のそれぞれについて再帰関数 search を呼び出す。引数の行と列には,移動先を指定する。移動順序には,現在の移動順序に 1 を加えたものを指定する。
- (ⅱ-3)
- 現在のマスの移動順序を取り消して,マスを通過していない状態に戻す。
- (ⅱ-4)
- 再帰関数 search の呼出し元へ戻る。
この処理の概要をプログラムに実装するために,M×Nマスの盤面,ナイトの移動先をそれぞれ次のデータ構造で表現することにした。
- M×Nマスの盤面を2次元配列 board[M][N] で表現する。添字は 1 から始まる。各要素の初期値は 0 とし,ナイトが通過した場合に,移動順序を各要素に格納する。
- ナイトの各移動先について,行方向,列方向,それぞれの移動量をdv[ ],dh[ ]の配列で表現する。添字は 1 から始まる。dv[ ],dh[ ]はそれぞれ,八つの要素をもち,図1の移動先①~⑧に対応する行方向,列方向の移動量を設定する。

M×Nマスのナイトの巡歴問題について,解法のプログラムを考える。
解法のプログラムで使用する定数,変数及び関数を表2に示す。

なお,左側の番号はプログラムの行番号を示す。

ナイトの移動先が盤面の範囲外となった場合の判定処理を簡略化するために,図6のように盤面をナイトが移動できるマスが全て含まれる範囲まで拡大して表現する。
この変更に合わせて①関数 printBoard の変更,②メインプログラムの変更,③再帰関数 search の一部の行の削除を同時に行うことによって,プログラムを短縮することができる。

広告
設問1
表1中のア,イに入れる適切な移動量を答えよ。
解答例・解答の要点
ア:2
イ:-2
イ:-2
解説
dv[]・dh[]は、ナイト(K)の各移動先に対応する移動量を保持する配列です。ナイトの移動先は、現在位置からの相対位置で以下の8種類になります。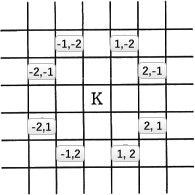
∴ア=2
イ=-2
広告
設問2
図3中のウ~キに入れる適切な字句を答えよ。
解答例・解答の要点
ウ:iがm×n
エ:i+1
オ:v+dv[j]
カ:h+dh[j]
キ:board[v] [h]←0
エ:i+1
オ:v+dv[j]
カ:h+dh[j]
キ:board[v] [h]←0
解説
〔ウについて〕printBoard を実行するときの条件式が入ります。printBoard は、解の1つが見つかったときにその解答を印字する関数です。
〔ナイトの巡歴問題の処理の概要〕では、「記録した移動順序がM×Nに等しい場合,その経路を解の一つとして出力する」という説明があります(M×Nは盤面上の全マス目数)。つまり、printBoard を実行するための条件式は、「現在の移動順序がM×Nに等しい場合」ということになります。現在の移動順序は関数 search の引数である i に格納されているので、ウに入る条件式は iがm×n(と等しい) が適切です。
※大文字のMとNは定数、小文字のmとnは変数ですが、プログラム中での使われ方は同じですので回答に当たってはどちらでも構わないと思われます。
∴ウ=iがm×n
〔エについて〕
再帰関数 search は以下のように定義されています。
再帰関数 search(移動順序,行,列)
search の第1引数には「移動順序」を指定することになっています。11行目の search は、次の移動先を調べるために実行されます。移動順序はナイトが移動するごとに 1 ずつ増えていくため、次の移動先を調べる際には現在の移動順序に 1 を加えた値を指定しなければなりません。現在の移動順序は i に格納されているので、エにはそれに 1 を加算した i+1 を指定することになります。
∴エ=i+1
〔オについて〕
search の第2引数には、調査対象となるマス目の行番号を指定します。〔処理の概要〕では、「現在のマスを起点として①~⑧移動先のそれぞれについて関数 search を呼び出す」と説明されています。10~12行目は、for文を用いた繰り返し処理で8方向について search を呼び出す処理に当たります。現在のマス目からの8つの移動量については配列 dv[] の1~8番目の要素として保持されているので、現在の行位置 v に 行方向の移動量 dv[j] を加えて、調査対象の行位置を指定することになります。
∴オ=v+dv[j]
〔カについて〕
search の第3引数には、調査対象となるマス目の列番号を指定します。行のときと同じ考え方で、現在の列位置 h に 列方向の移動量 dh[j] を加えて、列位置を指定することになります。
∴カ=h+dh[j]
〔キについて〕
プログラムのコメントに「移動順序を取り消す」とあるため、キにはそれに相当する処理が入ることがわかります。ここで、プログラムの5行目を見てみるとキと逆の「移動順序を記録する」処理が行われており、board[v][h] に移動順序の値 i を設定することにより記録していることに気付きます。board[][] の各要素の初期値は 0 ですから、board[v][h] に 0 を代入すれば移動順序の記録を取り消せることになります。以上よりキには board[v][h] ← 0 が入ると判断できます。
∴キ=board[v][h] ← 0
以下のこの問題のプログラムをJavaScriptで実装したものです。細かな動作の確認等にご使用ください。
広告
設問3
〔盤面の表現の変更〕について,(1)~(3)に答えよ。
解答例・解答の要点
- ①行番号:20
①変更後のプログラム:for(vを3からm+2まで1ずつ増やす)
②行番号:21
②変更後のプログラム:for(hを3からn+2まで1ずつ増やす)
- 行番号:32
変更後のプログラム:search(1, 3, 3)
- 2, 3, 16, 17
解説
- printBoard にて出力する部分は以下の図の白い部分です。しかし、printBoard の内容を変えずにそのまま実行すると、出力される部分は以下の赤枠で囲った部分になってしまいます。これはfor文の繰り返し条件が変更後の盤面に対応していないためです。
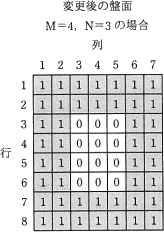 上記のM=4・N=3の例でいえば、繰り返し条件として行番号(縦方向)が3から6まで、列番号列(横方向)が3から5までになるべきです。行番号の終点である 6 は m=4 を用いて表すと m+2、列番号の終点 5 も同様に n+2 として表せるので、行番号・列番号ともに開始を 3 にし、行番号は m+2、列番号は n+2 までの繰り返しとすれば正しい出力範囲となります。
上記のM=4・N=3の例でいえば、繰り返し条件として行番号(縦方向)が3から6まで、列番号列(横方向)が3から5までになるべきです。行番号の終点である 6 は m=4 を用いて表すと m+2、列番号の終点 5 も同様に n+2 として表せるので、行番号・列番号ともに開始を 3 にし、行番号は m+2、列番号は n+2 までの繰り返しとすれば正しい出力範囲となります。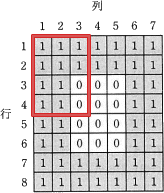
したがって printBoard 中の変更点は以下の2箇所です。//20行目
for (vを1からmまで1ずつ増やす)
↓
for (vを3からm+2まで1ずつ増やす)//21行目
for (hを1からnまで1ずつ増やす)
↓
for (hを3からn+2まで1ずつ増やす) - メインプログラムも盤面の拡大に対応させなくてはならない部分があります。最初の search 呼び出しは盤面の左上から始める必要がありますが、search(1, 1, 1)のままでは範囲外のマスから開始することになってしまいます。このため本来の盤面の左上に位置する行番号3・列番号3の位置から search を開始するように変更しなければなりません。よって変更箇所および内容は次の通りです。//32行目
search(1, 1, 1)
↓
search(1, 3, 3) - 範囲外の要素には1が格納されています。この理由は、範囲外のマスが調査対象になった場合でも4行目の「if (board[v][h]が0)」の条件式で偽と判定され、その後の処理を省略できるためです。従来は2・3行目のif文で調査対象のマスが範囲内かどうかをチェックしていましたが、変更後は盤面を拡大したことにより盤面外のマスが調査対象となることがなくなります。このため、vとhが適切な範囲に収まっているかどうかのチェックが不要になります。
以上より削除すべき行は、2・3行目の if文 及びその2つのif文に対応する16・17行目の endif と判断できます。
∴2, 3, 16, 17
広告

広告