令和6年春期試験午後問題 問3
問3 プログラミング
⇱問題PDF
グラフのノード間の最短経路を求めるアルゴリズムに関する次の記述を読んで設問に答えよ。
グラフのノード間の最短経路を求めるアルゴリズムに関する次の記述を読んで設問に答えよ。
広告
グラフ内の二つのノード間の最短経路を求めるアルゴリズムにダイクストラ法がある。このアルゴリズムは,車載ナビゲーションシステムなどに採用されている。
〔経路算定のモデル化〕
グラフは,有限個のノードの集合と,その中の二つのノードを結ぶエッジの集合とから成る数理モデルである。ダイクストラ法による最短経路の探索問題を考えるに当たり,本問では,エッジをどちらの方向にも行き来することができ,任意の二つのノード間に経路が存在するグラフを扱う。ここで,グラフを次のように定義する。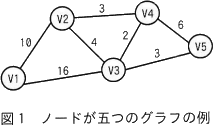 〔始点から終点までの最短距離を求める手順〕
〔始点から終点までの最短距離を求める手順〕
ダイクストラ法による始点から終点までの最短距離の算出は次のように行う。
最初に,各ノードについて,始点からそのノードまでの距離(以下,始点ノード距離という)を作業用に導入して十分に大きい定数としておく。ただし,始点の始点ノード距離は0とする。この時点では,どのノードの最短距離も確定していない。
次に,終点の最短距離が確定するまで,1~3を繰り返す。ここで,始点との距離を算出する基準となるノードを更新起点ノードという。
〔図1の例における最短距離を求める手順と始点ノード距離〕
図1の例において,始点V1から終点V5までの経路に対して,上の①~③を繰返し適用する。そのとき,更新起点ノードを選ぶたびに,更新起点ノードの始点ノード距離,更新起点ノードと隣接するノードの始点ノード距離,及び最短距離が確定していないノードの始点ノード距離を計算した内容を表1に示す。 〔最短距離の算出プログラム〕
〔最短距離の算出プログラム〕
始点から終点までの最短距離を求める関数 distance のプログラムを図2に示す。配列の要素番号は1から始まるものとする。また,行頭の数字は行の番号を表す。 〔最短経路の出力〕
〔最短経路の出力〕
関数 distance を変更して,求めた最短距離となる最短経路を出力できるようにする。具体的には,まず,ノード番号1~Nを格納する配列 viaNode を使用するために,図3の変数宣言を図2の行10の直後に,図4のプログラムを図2の行21の直後に,それぞれ挿入する。さらに,各ノードの始点ノード距離を更新するたびに,直前に経由したノード番号を viaNode に格納する①代入文を一つ,図2のプログラムの行オの直後に挿入する。
このプログラムの変更によって,終点のノード番号を起点としてカたどることで,最短経路のノード番号を逆順に出力する。
 〔計算量の考察〕
〔計算量の考察〕
関数 distance では,次のキを選ぶために始点ノード距離を計算する回数は最大でもN回である。また,キを選ぶ回数は,一度選ばれると当該ノードの最短距離は確定するので,最大でもN回である。よって,最悪の場合の計算量は,O(ク)である。
〔経路算定のモデル化〕
グラフは,有限個のノードの集合と,その中の二つのノードを結ぶエッジの集合とから成る数理モデルである。ダイクストラ法による最短経路の探索問題を考えるに当たり,本問では,エッジをどちらの方向にも行き来することができ,任意の二つのノード間に経路が存在するグラフを扱う。ここで,グラフを次のように定義する。
- ノードの個数をNとし,Nは2以上とする。ノードの番号(以下,ノード番号という)は,始点のノード番号を1とし,1から始まる連続した整数とする。ノードには,ノード番号に対応させて,V1,V2,V3,…,VNとラベルを付ける。
- 二つのノードが他のノードを経由せずにエッジでつながっているとき,それらのノードは隣接するという。隣接するノード間のエッジには,ノード間の距離として正の数値を付ける。
- 始点のノード(以下,始点という)とは別のノードを終点のノード(以下,終点という)として定める。始点からあるノードまでの経路の中から,経路に含まれるエッジに付けられた距離の和が最小の距離を最短距離という。始点から終点までの最短距離となる経路を最短経路という。

ダイクストラ法による始点から終点までの最短距離の算出は次のように行う。
最初に,各ノードについて,始点からそのノードまでの距離(以下,始点ノード距離という)を作業用に導入して十分に大きい定数としておく。ただし,始点の始点ノード距離は0とする。この時点では,どのノードの最短距離も確定していない。
次に,終点の最短距離が確定するまで,1~3を繰り返す。ここで,始点との距離を算出する基準となるノードを更新起点ノードという。
- 最短距離が確定していないノードの中で,始点ノード距離が最小のノードを更新起点ノードとして選び,そのときの始点ノード距離の値で,当該更新起点ノードの最短距離を確定する。更新起点ノードを選ぶ際に,始点ノード距離が最小となるノードが複数ある場合は,その中の任意のノードを更新起点ノードとして選ぶ。
- 更新起点ノードが終点であれば,終了する。
- ①で選択した更新起点ノードに隣接しており,かつ,最短距離が確定していない全てのノードについて,更新起点ノードを経由した場合の始点ノード距離を計算する。ここで計算した始点ノード距離が,そのノードの現在までの始点ノード距離よりも小さい場合には,そのノードの現在までの始点ノード距離を更新する。
〔図1の例における最短距離を求める手順と始点ノード距離〕
図1の例において,始点V1から終点V5までの経路に対して,上の①~③を繰返し適用する。そのとき,更新起点ノードを選ぶたびに,更新起点ノードの始点ノード距離,更新起点ノードと隣接するノードの始点ノード距離,及び最短距離が確定していないノードの始点ノード距離を計算した内容を表1に示す。

始点から終点までの最短距離を求める関数 distance のプログラムを図2に示す。配列の要素番号は1から始まるものとする。また,行頭の数字は行の番号を表す。

関数 distance を変更して,求めた最短距離となる最短経路を出力できるようにする。具体的には,まず,ノード番号1~Nを格納する配列 viaNode を使用するために,図3の変数宣言を図2の行10の直後に,図4のプログラムを図2の行21の直後に,それぞれ挿入する。さらに,各ノードの始点ノード距離を更新するたびに,直前に経由したノード番号を viaNode に格納する①代入文を一つ,図2のプログラムの行オの直後に挿入する。
このプログラムの変更によって,終点のノード番号を起点としてカたどることで,最短経路のノード番号を逆順に出力する。


関数 distance では,次のキを選ぶために始点ノード距離を計算する回数は最大でもN回である。また,キを選ぶ回数は,一度選ばれると当該ノードの最短距離は確定するので,最大でもN回である。よって,最悪の場合の計算量は,O(ク)である。
広告
設問1
表1中のアに入れる適切な字句を答えよ。
解答例・解答の要点
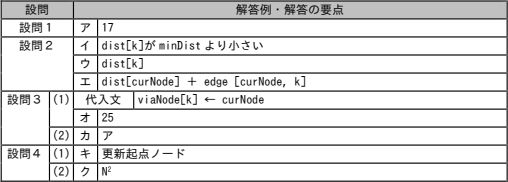
ア:17
解説
〔アについて〕表1の5回目では、終点であるV5が更新起点ノードとなり、始点ノードV1から終点ノードV5までの最短距離が確定しています。<>内の数値は、当該ノードの始点ノード距離を示すため、空欄アには始点ノードV1から終点ノードV5までの最短距離が入るはずです。図1を見ると、V1からV5までの最短距離は「V1→V2→V4→V5」で「10+4+3=17」なので、空欄aには「17」が当てはまります。
表1で終点ノードが確定するまでの手順を説明すると以下のようになります。
【1回目】
最短距離が確定していないノードの中で、始点ノード距離が最小のノードはV1<0>なので、V1までの最短距離が0で確定する。V1を更新起点ノードとして、隣接するV2、V3の始点距離ノードを計算すると、V1→V2が10、V1→V3が16なので、V2<10>、V3<16>のままとなる(更新なし)。
【2回目】
最短距離が確定していないノードの中で、始点ノード距離が最小のノードはV2<10>なので、V2までの最短距離が10で確定する。V2を更新起点ノードとして、隣接するV3、V4の始点距離ノードを計算すると、V2→V3が14、V2→V4が13なので、V3<14>、V4は<13>で更新される。
【3回目】
最短距離が確定していないノードの中で、始点ノード距離が最小のノードはV4<13>なので、V4までの最短距離が13で確定する。V4を更新起点ノードとして、隣接するV3、V5の始点距離ノードを計算すると、V4→V3が15、V4→V5が19なので、V5は<19>で更新される。
【4回目】
最短距離が確定していないノードの中で、始点ノード距離が最小のノードはV3<14>なので、V3までの最短距離が14で確定する。V3を更新起点ノードとして、隣接するV5の始点距離ノードを計算すると、V3→V5が17なので、V5は<17>で更新される。
【5回目】
最短距離が確定していないノードの中で、始点ノード距離が最小のノードはV5<17>なので、V5までの最短距離が17で確定する。V5は終点なので処理が終了する。
∴ア=17
広告
設問2
図2中のイ~エに入れる適切な字句を答えよ。
解答例・解答の要点
イ:dist[k]がminDistより小さい
ウ:dist[k]
エ:dist[curNode] + edge[curNode, k]
ウ:dist[k]
エ:dist[curNode] + edge[curNode, k]
解説
〔始点から終点までの最短距離を求める手順(以下、手順という)〕の①~③と〔最短距離の算出プログラム〕とは次のように対応しています。
2つの空欄は、手順①の更新起点ノードを選ぶ処理に関連しています。
14~19行目のfor文では次の処理を行っています。
- 1からN(ノード1からノードN)まで繰り返す
- if文がtrueであれば minDist と curNode を設定する
- 最短距離が確定していない
- 始点ノード距離が現在の最短距離よりも小さい
現在のノードの始点ノード距離は、6行目コメントより dist[k] で参照することができます。現在の最短距離は、その名称と使われ方より変数 minDist に保持されていると考えられるので、dist[k] と minDist を比較することになります。したがって、空欄イには dist[k]がminDistより小さい が当てはまります。
次に空欄ウについて考えます。
if文がtrueとなり curNode が変更される場合、その後の比較のために、そのノードの始点ノード距離を現在の最短距離として保持しておく必要があります。前述のとおり、現在の最短距離を保持する変数が minDist なので、minDist には「現在のノードの始点ノード距離」を格納することになります。したがって、空欄ウには dist[k] が当てはまります。
∴イ=dist[k]がminDistより小さい
ウ=dist[k]
〔エについて〕
空欄は、手順③の始点ノード距離を更新する処理に関連しています。
24~28行目のfor文では次の処理を行っています。
- 1からN(ノード1からノードN)まで繰り返す
- if文がtrueであれば dist[k] を設定する
- 最短距離が確定していない
- 更新起点ノードを経由した場合の始点ノード距離が、現在の始点ノード距離よりも小さい
更新起点ノードを経由した場合の始点ノード距離は、次の2つの合計値として求めることができます。
- 更新起点ノードの始点ノード距離 dist[curNode]
- 更新起点ノードから現在のノードまでの距離 edge[curNode, k]
なお、現在の更新起点ノードの始点ノード距離は、手順①の処理で minDist に格納されたままになっているので、dist[curNode] を minDist に変えても正しく動作します。
∴エ=dist[curNode] + edge[curNode, k]
広告
設問3
〔最短経路の出力〕について答えよ。
- 本文中の下線①とオについて,挿入すべき代入文とオに入れる行の番号を答えよ。行の番号については,最も小さい番号を答えること。ただし,図2中の現在の行の番号は図3及び図4の挿入によって変化しないものとする。
- 本文中の力に入れる適切な字句を解答群の中から選び,記号で答えよ。
カ に関する解答群
- viaNode に格納してあるノード番号を
- viaNode の要素番号を大きい方から
- viaNode の要素番号を小さい方から
解答例・解答の要点
- 代入文:viaNode[k] ← curNode
オ:25
- カ:ア
解説
- まず「各ノードの始点ノード距離を更新するたびに」とあるので、図2の中で始点ノード距離を更新している箇所を探します。すると、26行目のみで更新していることがわかります。この処理と同じタイミングで実行させたいので、代入文は25~27行目のif文内に挿入されるべきです。
次に挿入すべき代入文について考えます。
代入文は「直前に経由したノード番号を viaNode に格納するもの」です。挿入される箇所がif文内なので、現在のノードに対応する viaNode の要素はループ変数を使用して viaNode[k] で表せます。手順③で始点ノード距離を更新する際、"直前に経由するノード"に当たるのはそのときの更新起点ノードなので、格納すべきは curNode です。したがって、代入文は viaNode[k] ← curNode となります。
最後に挿入位置について考えます。
挿入位置は25~27行目のif文内であればよく、代入文と26行目の処理との間に依存関係はないので、25行目の直後でも26行目の直後でも正しく動作します。しかし、設問には「行の番号については,最も小さい番号を答える」という条件があるので、正解は「行25の直後」となります。
∴代入文=viaNode[k] ← curNode
オ=25 - 最短経路の出力は、終点のノード番号を起点として、ノード番号を逆順に出力するものです。例えば、図1のグラフでは最短経路が「V1→V2→V3→V5」なので、「5, 3, 2, 1」と出力することになります。これを図4のプログラムと突き合わせてみると、次のような流れでノード番号が出力されることがわかります。GOALを出力 //5要素番号の参照順は「5→3→2」です。小さい方から順でも、大きい方から順でもなく、終点ノードを起点として viaNode に格納されたノード番号をたどっていることがわかります。したがって「ア」が適切です。
j ← GOAL
viaNode[5]を出力 //3
j ← 3
viaNode[3]を出力 //2
j ← 2
viaNode[2]を出力 //1
j ← 1
jが1なのでwhileループが終了
∴カ=ア:viaNode に格納してあるノード番号を
広告
設問4
〔計算量の考察〕について答えよ。
- 本文中のキに入れる適切な字句を,本文中の字句を用いて10字以内で答えよ。
- 本文中のクに入れる適切な字句を答えよ。
解答例・解答の要点
- キ:更新起点ノード (7文字)
- ク:N2
解説
〔キについて〕「キを選ぶ回数は,一度選ばれると当該ノードの最短距離は確定するので…」とあるので、最短距離が確定するときに選ばれるものを考えます。手順①には「始点ノード距離が最小のノードを更新起点ノードとして選び,そのときの始点ノード距離の値で,当該更新起点ノードの最短距離を確定する」とあるため、これに該当するのは「更新起点ノード」であることがわかります。
∴キ=更新起点ノード
〔クについて〕
〔計算量の考察〕には「次の【キ:更新起点ノード】を選ぶために始点ノード距離を計算する回数は最大でもN回である」とあります。これは手順③に対応します。手順③は最大でN回実行されるため、計算量(オーダ)はO(N)です。同様に、手順①も最大でN回実行されるfor文を含むので、計算量はO(N)です。手順②は繰返し処理がないのでO(1)です。以上より、手順①~③を1回実行した場合の計算量は、O(N)+O(1)+O(N) ⇒ O(N) となります(オーダ記法では定数は無視します)。
また「【キ:更新起点ノード】を選ぶ回数は,一度選ばれると当該ノードの最短距離は確定するので,最大でもN回である」とあります。これは、更新起点ノードを1つ選ぶごとに1回実行されるwhile文の繰返しに対応します。while文は最大でN回実行されるため、計算量はO(N)です。
関数 distance のプログラムは、while文の中に2つのfor文が含まれる構造をしています。最大でN回繰り返すwhile文の中に、最大でN回繰り返すfor文があるため、このプログラムのオーダは O(N)×O(N) ⇒ O(N2) になります。したがって、空欄クには「N2」が入ります。
∴ク=N2
広告
広告