平成20年春期試験問題 午前問13
問13解説へ
次の流れ図において,ステップS4でYesと判断したときまでの,ステップS1~S4の実行回数をそれぞれn1~n4とする。n1~n4の間に成立する式はどれか。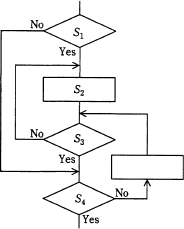

- n4=n1+n2+n3
- n4=n1+n2-n3
- n4=n1-n2+n3
- n4=-n1+n2+n3
広告
解説
まず、S1~S4までを1回ずつ実行した次のケースを考えてみます。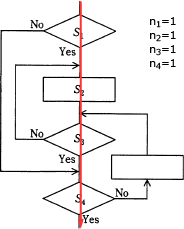
「イ」と「ウ」で異なる部分は"+n2-n3"と"-n2+n3"だけで、n2とn3の実行回数が同じ時には2つの式の結果に違いが現れないため、n2とn3が異なる実行回数をとる次のようなケースで検証を行います。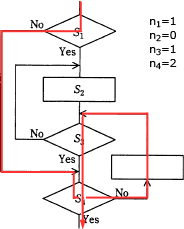

- 1=1+1+1 で成立しません。
- 1=1+1-1 で成立します。
- 1=1-1+1 で成立します。
- 1=-1+1+1 で成立します。
「イ」と「ウ」で異なる部分は"+n2-n3"と"-n2+n3"だけで、n2とn3の実行回数が同じ時には2つの式の結果に違いが現れないため、n2とn3が異なる実行回数をとる次のようなケースで検証を行います。

- 「イ」2=1+0-1 で成立しません。
- 「ウ」2=1-0+1 で成立します。
- 「エ」2=-1+0+1 で成立しません。
広告