平成20年春期試験問題 午前問5
問5解説へ
XとYの否定論理積 X NAND Y は,NOT(X AND Y)として定義される。X OR Y をNANDだけを使って表した論理式はどれか。
- ((X NAND Y) NAND X) NAND Y
- (X NAND X) NAND (Y NAND Y)
- (X NAND Y) NAND (X NAND Y)
- X NAND (Y NAND (X NAND Y))
広告
解説
否定論理積(NAND)は、2つの入力がともに1の場合にだけ結果が0、その他の場合は1となる論理演算です。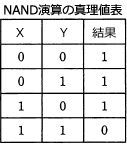 X OR Yは、下の真理値表で表される論理演算なので、これをもとに各選択肢のXとYに0または1を代入してOR演算と同様の結果になるかを検証していきます。
X OR Yは、下の真理値表で表される論理演算なので、これをもとに各選択肢のXとYに0または1を代入してOR演算と同様の結果になるかを検証していきます。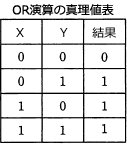 まずX=0,Y=0のときに演算結果が0になるかを検証します。
まずX=0,Y=0のときに演算結果が0になるかを検証します。
また4つの論理式をベン図で表すと次のようになります。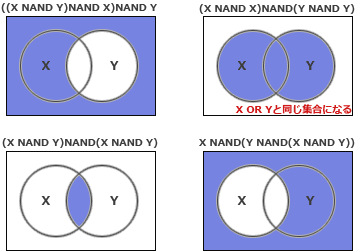 こちらの方法でも正解を導くことが可能です。
こちらの方法でも正解を導くことが可能です。


- ((0 NAND 0)NAND 0)NAND 0
=(1 NAND 0) NAND 0
=1 NAND 0
=1
結果が0ではないので誤りとわかります。 - (0 NAND 0)NAND(0 NAND 0)
=1 NAND 1
=0
結果が0なので正しい可能性があります。 - (0 NAND 0)NAND(0 NAND 0)
=1 NAND 1
=0
結果が0なので正しい可能性があります。 - 0 NAND(0 NAND(0 NAND 0))
=0 NAND (0 NAND 1)
=0 NAND 1
=1
結果が0ではないので誤りとわかります。
- 「イ」
(1 NAND 1) NAND (0 NAND 0)
=0 NAND 1
=1 - 「ウ」
(1 NAND 0) NAND (1 NAND 0)
=1 NAND 1
=0
結果が1ではないので誤りとわかります。
また4つの論理式をベン図で表すと次のようになります。

広告