平成19年秋期試験問題 午前問6
は論理積(AND)，
は論理和(OR)，
は否定論理積(NAND)，
は否定論理和(NOR)を表す。
広告
解説
集合演算則を用いて解く方法と、ベン図を用いて解く方法の2通りを解説します。
[集合演算則を用いた解法]
A・B＋A・B＋A・B
＝ A・(B＋B)＋A・B //第1項と第3項をAでくくる
＝ A＋A・B //B＋Bは1，1・X＝X
＝ A・(A＋B) //ド・モルガン則を逆に適用する
＝ A・A＋A・B //分配の法則
＝ A・B //A・Aは0，0＋X＝X
A・Bは、NAND(not AND)回路の出力と同じなので正解は「イ」になります。
[ベン図を用いた解法]
第1項～第3項の論理式をベン図で表すと次のようになります。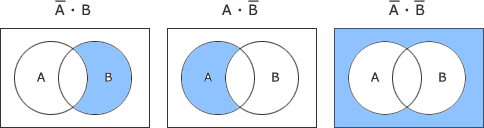
これら3つの集合の論理和をベン図で表すと以下のようになり、NANDを示しているため、正解は「イ」ということになります。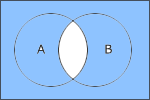
[集合演算則を用いた解法]
A・B＋A・B＋A・B
＝ A・(B＋B)＋A・B //第1項と第3項をAでくくる
＝ A＋A・B //B＋Bは1，1・X＝X
＝ A・(A＋B) //ド・モルガン則を逆に適用する
＝ A・A＋A・B //分配の法則
＝ A・B //A・Aは0，0＋X＝X
A・Bは、NAND(not AND)回路の出力と同じなので正解は「イ」になります。
[ベン図を用いた解法]
第1項～第3項の論理式をベン図で表すと次のようになります。
広告