応用数学 (全55問中2問目)
No.2
複数の袋からそれぞれ白と赤の玉を幾つかずつ取り出すとき,ベイズの定理を利用して事後確率を求める場合はどれか。
出典:令和6年春期 問1
- ある袋から取り出した二つの玉の色が同じと推定することができる確率を求める場合
- 異なる袋から取り出した玉が同じ色であると推定することができる確率を求める場合
- 玉を一つ取り出すために,ある袋が選ばれると推定することができる確率を求める場合
- 取り出した玉の色から,どの袋から取り出されたのかを推定するための確率を求める場合
分類
テクノロジ系 » 基礎理論 » 応用数学
正解
エ
解説
ベイズの定理は、ある条件付確率の結果を基にして、その事象が前提とする条件が起こっていた確率(事後確率)を計算するために使用される次の式です。
P(B|A)=P(A|B)×P(B)P(A)
P(原因|結果)=P(結果|原因)×P(原因)P(結果)
例えば袋が2つあり、袋1には白玉5つと赤玉3つ、袋2には白玉2つと赤玉8つが入っているとします。2つの袋のどちらが選ばれるかは同様に確からしいとすると、玉を1つ取り出しそれが赤玉だった場合、
P(袋1|赤玉)=3/8×1/21/2×3/8+1/2×8/10
=3/163/16+4/10=3/1647/80=15/47
逆に袋2から選ばれた確率 P(袋2|赤玉) は、1-15/47=32/47
このように結果データから原因が起こった確率を求めることができるのがベイズの定理です。ベイズの定理は、機械学習やデータサイエンスにおける多くのアルゴリズムや手法の基礎となっています。したがって「エ」が正解となります。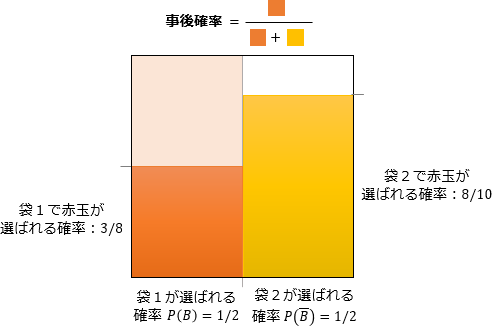
P(B|A)=P(A|B)×P(B)P(A)
- P(A|B) Bが起きたという条件の下でAが起こる確率:事後確率
- P(B|A) Aが起きたという条件の下でBが起こる確率:尤度(ゆうど)
- P(B) Bが起こる確率:事前確率
- P(A) Aが起こる確率:周辺尤度
P(原因|結果)=P(結果|原因)×P(原因)P(結果)
例えば袋が2つあり、袋1には白玉5つと赤玉3つ、袋2には白玉2つと赤玉8つが入っているとします。2つの袋のどちらが選ばれるかは同様に確からしいとすると、玉を1つ取り出しそれが赤玉だった場合、
- P(B|A) 袋1が選ばれ赤玉が取り出される確率:1/2×3/8=3/16
- P(B) 袋1が選ばれる確率:1/2
- P(A) 赤玉が取り出される確率:1/2×3/8+1/2×8/10
P(袋1|赤玉)=3/8×1/21/2×3/8+1/2×8/10
=3/163/16+4/10=3/1647/80=15/47
逆に袋2から選ばれた確率 P(袋2|赤玉) は、1-15/47=32/47
このように結果データから原因が起こった確率を求めることができるのがベイズの定理です。ベイズの定理は、機械学習やデータサイエンスにおける多くのアルゴリズムや手法の基礎となっています。したがって「エ」が正解となります。

