応用数学 (全55問中26問目)
No.26
三つのグラフA～Cの同形関係に関する記述のうち，適切なものはどれか。ここで，二つのグラフが同形であるとは，一方のグラフの頂点を他方のグラフの頂点と1対1に漏れなく対応付けることができ，一方のグラフにおいて辺でつながれている頂点同士は他方のグラフにおいても辺でつながれていて，一方のグラフにおいて辺でつながれていない頂点同士は他方のグラフにおいても辺でつながれていないことをいう。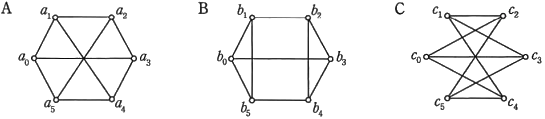
出典：平成26年春期 問2
- AはCと同形であるが，Bとは同形でない。
- BはCと同形であるが，Aとは同形でない。
- どの二つのグラフも同形である。
- どの二つのグラフも同形でない。
分類
テクノロジ系 » 基礎理論 » 応用数学
正解
ア
解説
グラフAとグラフBは、a1とb1，a2とb2というようにそれぞれの頂点が対応していますが、グラフAではa1－a4，a2－a5の頂点同士が辺でつながれているのに対して、グラフBは繋がれていないため同形ではありません。
グラフAとグラフCですが、下図のように グラフAのa0がグラフCのc3に、a3がc0にそれぞれ移動したと考えると、頂点と辺の両方が完全に一致していることになります。つまり頂点の位置が異なるだけでグラフAとグラフCは同形であると言えます。
グラフBとグラフCは、グラフCがグラフAと同形であることから同形ではないことになります。
したがって正しい記述は「ア」です。
グラフAとグラフCですが、下図のように グラフAのa0がグラフCのc3に、a3がc0にそれぞれ移動したと考えると、頂点と辺の両方が完全に一致していることになります。つまり頂点の位置が異なるだけでグラフAとグラフCは同形であると言えます。
したがって正しい記述は「ア」です。