応用数学 (全55問中32問目)
No.32
連立一次方程式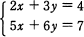
から，xの項の係数，yの項の係数，及び定数項だけを取り出した表(行列)を作り，基本操作(1)～(3)のいずれかを順次施すことによって，解
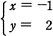が得られた。表(行列)が次のように左から右に推移する場合，同じ種類の基本操作が施された箇所の組合せはどれか。
〔基本操作〕
〔基本操作〕
- ある行に0でない数を掛ける。
- ある行と他の行を入れ替える。
- ある行に他の行の定数倍を加える。
出典：平成22年春期 問4
- a と b
- a と c
- b と c
- b と d
分類
テクノロジ系 » 基礎理論 » 応用数学
正解
イ
解説
a～dの各段階の処理について、基本操作の(1)～(3)のどれに相当するかを考えます。
- 上の行の値は変わらずに、下の行の値が1つ前の行列の値からそれぞれ－4、－6、－8されています。下の行の値は、それぞれ元の値に上の行の値（2、3、4）の－2倍を加算することで得られるので、基本操作の(3)に当たります。
- 上下の行を入れ替えているので、基本操作の(2)に当たります。
- 上の行の値は変わらずに、下の行の値が1つ前の行列の値から左の列からそれぞれ－2、±0、＋2されています。aと同じで、下の行の値は、それぞれ元の値に上の行の値（1、0、－1）の－2倍の値を加算することで得られるので、基本操作の(3)に当たります。
- 上の行の値は変わらずに、下の行の値がそれぞれ1／3になっているので、基本操作の(1)に当たります。