応用数学 (全55問中37問目)
No.37
関数y=ƒ(x)上の点(x0,ƒ(x0))における接線とx軸との交点のx座標をx1とする。x0とx1の関係式はどれか。ここで,ƒ'(x)はƒ(x)の導関数である。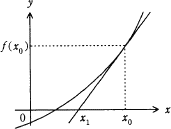

出典:平成20年秋期 問3
- x1=ƒ'(x0)-ƒ(x0)
- x1=ƒ(x0)-ƒ'(x0)
- x1=x0-ƒ'(x0)ƒ(x0)
- x1=x0-ƒ(x0)ƒ'(x0)
分類
テクノロジ系 » 基礎理論 » 応用数学
正解
エ
解説
導関数 ƒ'(x) に定数を代入した値 ƒ'(x0) を微分係数といい、これは接線の傾きを表します。
ここで、傾きの定義を考えます。xy平面上における直線の傾きは、yの変化量÷xの変化量で定義されています。この問題の接線は (x1, 0) と (x0, ƒ(x0)) を通る直線なので、yの変化量を ƒ(x0)-0、xの変化量を x0-x1 とすれば、
ƒ'(x0)=ƒ(x0)x0-x1
となり、これを以下のように変形すると、
ƒ'(x0)=ƒ(x0)x0-x1
ƒ'(x0)(x0-x1)=ƒ(x0)
x0-x1=ƒ(x0)ƒ'(x0)
-x1=ƒ(x0)ƒ'(x0)-x0
x1=x0-ƒ(x0)ƒ'(x0)
「エ」の関係式 x1=x0-ƒ(x0)ƒ'(x0) となります。
ここで、傾きの定義を考えます。xy平面上における直線の傾きは、yの変化量÷xの変化量で定義されています。この問題の接線は (x1, 0) と (x0, ƒ(x0)) を通る直線なので、yの変化量を ƒ(x0)-0、xの変化量を x0-x1 とすれば、
ƒ'(x0)=ƒ(x0)x0-x1
となり、これを以下のように変形すると、
ƒ'(x0)=ƒ(x0)x0-x1
ƒ'(x0)(x0-x1)=ƒ(x0)
x0-x1=ƒ(x0)ƒ'(x0)
-x1=ƒ(x0)ƒ'(x0)-x0
x1=x0-ƒ(x0)ƒ'(x0)
「エ」の関係式 x1=x0-ƒ(x0)ƒ'(x0) となります。
