アルゴリズム (全101問中100問目)
No.100
次の流れ図を実行したとき，手続が終了するまでに何回の比較を行うか。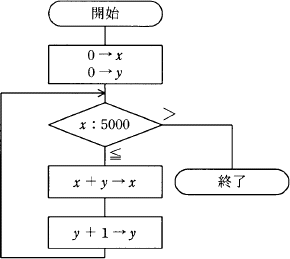
出典：平成17年春期 問14
- 99
- 100
- 101
- 102
分類
テクノロジ系 » アルゴリズムとプログラミング » アルゴリズム
正解
エ
解説
流れ図をトレースしていくと比較後に行われる処理によって変数xの値は下表に示すように増加していきます。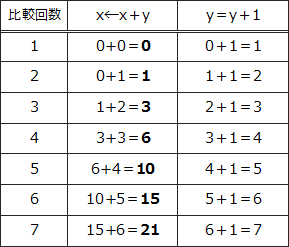
比較条件となるxに注目すると以下のような規則性に従って増加していることに気が付きます。
1～10までの和が、
1＋2＋3＋4＋5＋6＋7＋8＋9＋10
＝(1＋10)＋(2＋9)＋(3＋8)＋(4＋7)＋(5＋6)
＝11×5
＝55
として計算できるように、1～nまでの和は、
1＋2＋3＋…＋n
＝(1＋n)×(n÷2)
＝n(n＋1)／2
という式で表すことができます。
nに適当な値を代入し「n(n＋1)／2＞5000」となる閾値を考えると、n＝100 の時点で式の値が5050となり5000を超えることがわかります。
99(99＋1)／2＝99×100÷2＝4950
100(100＋1)／2＝100×101÷2＝5050
101(101＋1)／2＝101×102÷2＝5151
上の表から考えるとxの値が「1＋2＋3＋…＋100」と同値になるのは101回目比較後の処理時となり、ループを抜け手続きが終了するのは次の102回目の比較後になります。
したがって手続きが終了するまでに行われる比較回数はに102回が適切です。
- (1回目) 0＝0
- (2回目) 1＝1
- (3回目) 3＝1＋2
- (4回目) 6＝1＋2＋3
- (5回目) 10＝1＋2＋3＋4
- (6回目) 15＝1＋2＋3＋4＋5
- (7回目) 21＝1＋2＋3＋4＋5＋6
- x＝1＋2＋3＋…n
1～10までの和が、
1＋2＋3＋4＋5＋6＋7＋8＋9＋10
＝(1＋10)＋(2＋9)＋(3＋8)＋(4＋7)＋(5＋6)
＝11×5
＝55
として計算できるように、1～nまでの和は、
1＋2＋3＋…＋n
＝(1＋n)×(n÷2)
＝n(n＋1)／2
という式で表すことができます。
nに適当な値を代入し「n(n＋1)／2＞5000」となる閾値を考えると、n＝100 の時点で式の値が5050となり5000を超えることがわかります。
99(99＋1)／2＝99×100÷2＝4950
100(100＋1)／2＝100×101÷2＝5050
101(101＋1)／2＝101×102÷2＝5151
上の表から考えるとxの値が「1＋2＋3＋…＋100」と同値になるのは101回目比較後の処理時となり、ループを抜け手続きが終了するのは次の102回目の比較後になります。
したがって手続きが終了するまでに行われる比較回数はに102回が適切です。