アルゴリズム (全101問中97問目)
No.97
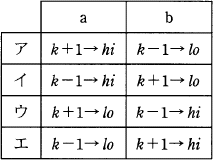
昇順に整列されたn個のデータが格納されている配列Aがある。流れ図は,配列Aからデータxを2分探索法を用いて探し出す処理を表している。a,bに入る操作の正しい組合せはどれか。ここで,除算の結果は小数点以下が切り捨てられる。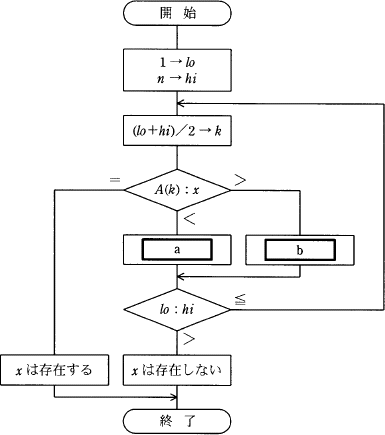

出典:平成17年春期 問11
- [出題歴]
- 基本情報技術者 H19秋期 問14
分類
テクノロジ系 » アルゴリズムとプログラミング » アルゴリズム
正解
ウ
解説
2分探索法は、要素が昇順または降順に整列された集合に対して、探索範囲の中央に位置する値と探索する値を比較し、探索する値の方が小さければ目的の値は範囲の先頭から中央までに、探索する値の方が大きければ目的の値は範囲の中央から最後までに存在すると判断して、次回は探索範囲を1/2に狭めて探索することを再帰的に繰返すことで目的のデータを探索するアルゴリズムです。
a,bの上の条件分岐は、探索範囲の中央に位置する値"A(k)"と探索する値"x"を比較している部分です。aは、A(k)<x(中央値より探索対象が大きい)の場合の処理で、探索対象はk以下に存在しないので探索範囲の下限値loにk+1を代入して探索範囲を1/2に狭めます。bは、逆にA(k)>x(中央値より探索対象が小さい)の場合の処理なので、探索範囲の上限値hiにk-1を代入して探索範囲を1/2に狭めます。
まとめると、
a(A(k)<x)=k+1→lo,
b(A(k)>x)=k-1→hi
なので「ウ」が適切な処理です。
a,bの上の条件分岐は、探索範囲の中央に位置する値"A(k)"と探索する値"x"を比較している部分です。aは、A(k)<x(中央値より探索対象が大きい)の場合の処理で、探索対象はk以下に存在しないので探索範囲の下限値loにk+1を代入して探索範囲を1/2に狭めます。bは、逆にA(k)>x(中央値より探索対象が小さい)の場合の処理なので、探索範囲の上限値hiにk-1を代入して探索範囲を1/2に狭めます。
まとめると、
a(A(k)<x)=k+1→lo,
b(A(k)>x)=k-1→hi
なので「ウ」が適切な処理です。