HOME»オリジナル模擬試験2»問7
オリジナル模擬試験2 問7
問7
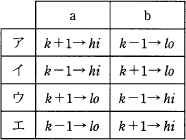
昇順に整列されたn個のデータが格納されている配列Aがある。流れ図は,配列Aからデータxを2分探索法を用いて探し出す処理を表している。a,bに入る操作の正しい組合せはどれか。ここで,除算の結果は小数点以下が切り捨てられる。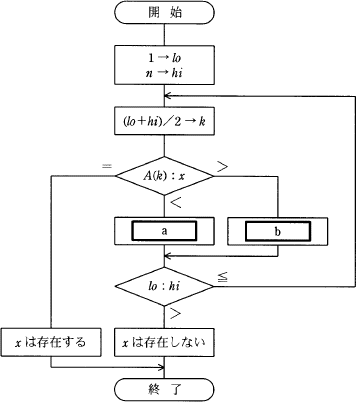

- [出典]
- 基本情報技術者 H19秋期 問14
分類
テクノロジ系 » アルゴリズムとプログラミング » データ構造
正解
ウ
解説
2分探索法は、要素が昇順または降順に整列された集合に対して、探索範囲を1/2に狭めることを繰り返して目的のデータを探索するアルゴリズムです。
2分探索法では目的とする値が与えられると、まず探索範囲の中央に位置する値と目的値を比較します。そして目的値の方が小さければ中央から探索範囲の最後までを、目的値の方が大きければ探索範囲の最初から中央まで探索範囲から除外して、探索範囲を1/2にします。そして再度、新たな探索範囲の中央値と目的値を比較して探索範囲を半分にする、というように同じ操作を再帰的に繰り返します。
この流れ図では変数loが配列中で探索範囲の先頭となる添え字、変数hiが配列中で探索範囲の最後となる添え字を保持しています。ループの先頭 (lo+hi)/2→k で kに探索範囲の中央となる添え字を設定し、A(k):xの分岐条件として探索範囲の中央値とxを比較しています。
aは、中央値よりxが大きかった時[A(k)<x]の処理で次回の探索範囲を中央から最後までにしたいので、最後を示す変数hiはそのままに変数loにk+1を設定します。つまりaには「k+1→lo」が入ります。
bは、中央値よりxが小さかった時[A(k)>x]の処理で次回の探索範囲を先頭から中央までにしたいので、先頭を示す変数loはそのままに変数hiにk-1を設定します。つまりaには「k-1→hi」が入ります。
2分探索法では目的とする値が与えられると、まず探索範囲の中央に位置する値と目的値を比較します。そして目的値の方が小さければ中央から探索範囲の最後までを、目的値の方が大きければ探索範囲の最初から中央まで探索範囲から除外して、探索範囲を1/2にします。そして再度、新たな探索範囲の中央値と目的値を比較して探索範囲を半分にする、というように同じ操作を再帰的に繰り返します。
この流れ図では変数loが配列中で探索範囲の先頭となる添え字、変数hiが配列中で探索範囲の最後となる添え字を保持しています。ループの先頭 (lo+hi)/2→k で kに探索範囲の中央となる添え字を設定し、A(k):xの分岐条件として探索範囲の中央値とxを比較しています。
aは、中央値よりxが大きかった時[A(k)<x]の処理で次回の探索範囲を中央から最後までにしたいので、最後を示す変数hiはそのままに変数loにk+1を設定します。つまりaには「k+1→lo」が入ります。
bは、中央値よりxが小さかった時[A(k)>x]の処理で次回の探索範囲を先頭から中央までにしたいので、先頭を示す変数loはそのままに変数hiにk-1を設定します。つまりaには「k-1→hi」が入ります。