HOME»応用情報技術者平成23年秋期»午前問8
応用情報技術者平成23年秋期 午前問8
問8
データが昇順にソートされた配列X[i] (i=0,1,…,n-1)を2分探索する。流れ図のaに入るものとして,適切なものはどれか。ここで,流れ図の中の割り算は小数点以下を切り捨てるものとする。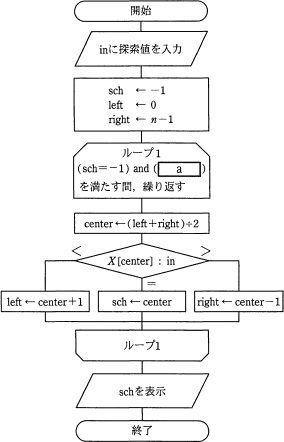

- left<right
- left≦right
- left+1<right
- left+1≦right
分類
テクノロジ系 » アルゴリズムとプログラミング » アルゴリズム
正解
イ
解説
2分探索法は、要素が昇順または降順に整列された集合に対して、探索範囲の中央に位置する値と探索する値を比較し、探索する値の方が小さければ目的の値は範囲の先頭から中央の1つ前までに、探索する値の方が大きければ目的の値は範囲の中央の1つ次から最後までに存在すると判断して、次回は探索範囲を1/2に狭めて探索することを再帰的に繰返すことで目的のデータを探索するアルゴリズムです。
ループの継続にかかわる変数schは、X[center]=in (探索値が見つかった)となったときに探索値を保持している配列の添え字を格納する役割を持ちます。探索値が配列の中にない場合には変数schは-1から変化しないので、aには、この場合に探索終了を判断しループを終了するための条件文が入ることになります。
探索値が存在しない配列に対して2分探索法による探索が進むと「left=5,right=6」というようにleftとrightが隣り合うまで探索範囲が狭まってきます。この状態からの処理の流れは、
ループの継続にかかわる変数schは、X[center]=in (探索値が見つかった)となったときに探索値を保持している配列の添え字を格納する役割を持ちます。探索値が配列の中にない場合には変数schは-1から変化しないので、aには、この場合に探索終了を判断しループを終了するための条件文が入ることになります。
探索値が存在しない配列に対して2分探索法による探索が進むと「left=5,right=6」というようにleftとrightが隣り合うまで探索範囲が狭まってきます。この状態からの処理の流れは、
left=5,right=6
center←(5+6)÷2=5
X[5]<in
left=5+1=6
この時点でleft,rightが同じ値なりますがX[6]とinの比較がまだ行われていないためループは継続する必要があります。center←(5+6)÷2=5
X[5]<in
left=5+1=6
left=6,right=6
center←(6+6)÷2=6
X[6]>in
right=6-1=5
このように、この流れ図では探索値が存在しなかった場合には「left>right」の状態になります。rightがleftより小さくなった場合には探索終了なので、ループを継続する条件はrightがleft以上、つまりaの文は「left≦right」が適切です。center←(6+6)÷2=6
X[6]>in
right=6-1=5
