HOME»応用情報技術者平成27年秋期»午前問6
応用情報技術者平成27年秋期 午前問6
問6
次に示すユークリッド互除法(方法1,方法2)で,正の整数 a,b の最大公約数は,それぞれmとnのどちらの変数に求まるか。ここで,m mod n はmをnで割った余りを表す。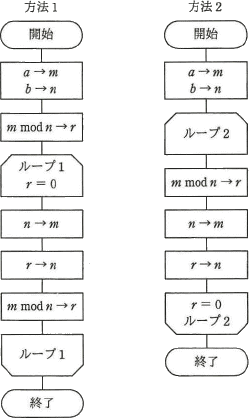

- [出題歴]
- ソフトウェア開発技術者 H18秋期 問13
- ソフトウェア開発技術者 H20秋期 問14
分類
テクノロジ系 » アルゴリズムとプログラミング » アルゴリズム
正解
ウ
解説
2つの方法で、a=256、b=160、最大公約数32 を設定した場合の流れをトレースしてみます。
[方法1]
[方法2]
したがって方法1では変数n、方法2では変数mに求まることになります。
[方法1]
m=256; n=160
256 mod 160=96 //r=96
[--ループ1回目--]
160→m; 96→n
160 mod 96=64 //r=64
[--ループ2回目--]
96→m; 64→n
96 mod 64=32 //r=32
[--ループ3回目--]
64→m; 32→n
64 mod 32=0 //r=0
[--ループ終了--]
終了時点でm=64、n=32なので最大公約数は変数nに格納されます。256 mod 160=96 //r=96
[--ループ1回目--]
160→m; 96→n
160 mod 96=64 //r=64
[--ループ2回目--]
96→m; 64→n
96 mod 64=32 //r=32
[--ループ3回目--]
64→m; 32→n
64 mod 32=0 //r=0
[--ループ終了--]
[方法2]
m=256; n=160
[--ループ1回目--]
256 mod 160=96 //r=96
160→m; 96→n
[--ループ2回目--]
160 mod 96=64 //r=64
96→m; 64→n
[--ループ3回目--]
96 mod 64=32 //r=32
64→m; 32→n
[--ループ4回目--]
64 mod 32=0 //r=0
32→m; 0→n
[--r=0でループ終了--]
終了時点でm=32、n=0なので最大公約数は変数mに格納されます。[--ループ1回目--]
256 mod 160=96 //r=96
160→m; 96→n
[--ループ2回目--]
160 mod 96=64 //r=64
96→m; 64→n
[--ループ3回目--]
96 mod 64=32 //r=32
64→m; 32→n
[--ループ4回目--]
64 mod 32=0 //r=0
32→m; 0→n
[--r=0でループ終了--]
したがって方法1では変数n、方法2では変数mに求まることになります。