HOME»応用情報技術者平成26年秋期»午前問4

応用情報技術者平成26年秋期 午前問4

問4

配列A[1]，A[2]，…，A[n]でA[1]を根とし，A[i]の左側の子をA[2i]，右側の子をA[2i＋1]とみなすことによって，2分木を表現する。このとき，配列を先頭から順に調べていくことは，2分木の探索のどれに当たるか。
  • 行きがけ順(先行順)深さ優先探索
  • 帰りがけ順(後行順)深さ優先探索
  • 通りがけ順(中間順)深さ優先探索
  • 幅優先探索
  • [出題歴]
  • 応用情報技術者 R3春期 問6
  • 応用情報技術者 H29秋期 問5
  • ソフトウェア開発技術者 H17秋期 問10
  • ソフトウェア開発技術者 H19春期 問10

分類

テクノロジ系 » アルゴリズムとプログラミング » データ構造

正解

エ

解説

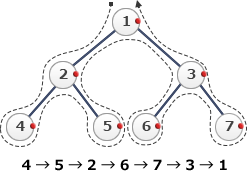
仮に配列[1, 2, 3, 4, 5, 6, 7]があったとき、設問のルールにより表される2分木は次の構造になります。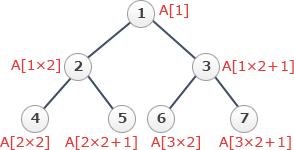
04_1.png/image-size:294×150
この木構造において配列を先頭から順に1，2，…と調べていくと、以下の順序で要素を調べていくことなります。
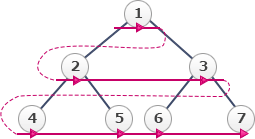04_2.png/image-size:255×139
根から近い順に階層ごとに探索することになるため「幅優先探索」が適切となります。よって「エ」が正解です。

なお、深さ優先探索は、根から開始して左の（右の）部分木優先で最も深い葉まで到達してから、一つ前の節まで戻り他方の部分木の探索を行うことを繰り返す方法です。先行順、後行順、中間順は参照するタイミングが違うだけです。
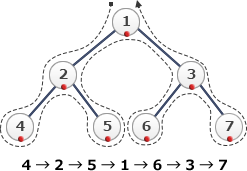
  • 行きがけ順(先行順) … 訪問したタイミングで調べる
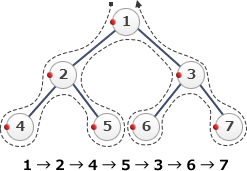
    04_3.png/image-size:247×171
  • 帰りがけ順(後行順) … 移動する子がなくなったタイミングで調べる
    04_4.png/image-size:247×171
  • 通りがけ順(中間順) … 左の子に移動できなくなったタイミングで調べる
    04_5.png/image-size:247×171
© 2010-2024　応用情報技術者試験ドットコム　All Rights Reserved.
▲
Pagetop