応用情報技術者過去問題 令和3年春期 午後問3
⇄問題文と設問を画面2分割で開く⇱問題PDF問3 プログラミング
クラスタ分析に用いるk-means法に関する次の記述を読んで，設問1～3に答えよ。
k-means法によるクラスタ分析は，異なる性質のものが混ざり合った母集団から互いに似た性質をもつものを集め，クラスタと呼ばれる互いに素な部分集合に分類する手法である。新聞記事のビッグデータ検索，店舗の品ぞろえの分類，教師なし機械学習などで利用されている。ここでは，2次元データを扱うこととする。
〔分類方法と例〕
N個の点をK個(N未満)のクラスタに分類する方法を(1)～(5)に示す。
P1＝(1，0) P2＝(2，1) P3＝(4，1) P4＝(1.5，2) P5＝(1，3) P6＝(2，3) P7＝(4，3)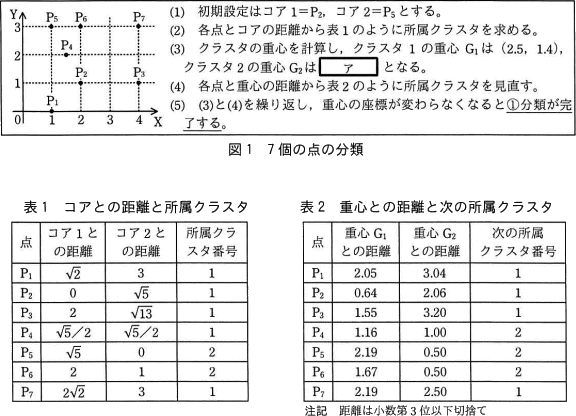
〔クラスタ分析のプログラム〕
この手法のプログラムを図2に，プログラムで使う主な変数，関数及び配列を表3に示す。ここで，配列の添字は全て1から始まり，要素の初期値は全て0とする。
〔初期設定の改良〕
このアルゴリズムの最終結果は初期設定に依存し，そこでのコア間の距離が短いと適切な分類結果を得にくい。そこで，関数 initial において一つ目のコアはランダムに選び，それ以降はコア間の距離が長くなる点が選ばれやすくなるアルゴリズムを検討した。検討したアルゴリズムでは，t番目までのコアが決まった後，t＋1番目のコアを残った点から選ぶときに，それまでに決まったコアから離れた点を，より高い確率で選ぶようにする。具体的には，それまでに決まったコア(コア1～コアt)と，残ったN－t個の点から選んだ点Psとの距離の和をTsとする。N－t個の全ての点についてTsを求め，Tsがカほど高い確率で点Psが選ばれるようにする。このとき，点Psがt＋1番目のコアとして選ばれる確率としてキを適用する。
k-means法によるクラスタ分析は，異なる性質のものが混ざり合った母集団から互いに似た性質をもつものを集め，クラスタと呼ばれる互いに素な部分集合に分類する手法である。新聞記事のビッグデータ検索，店舗の品ぞろえの分類，教師なし機械学習などで利用されている。ここでは，2次元データを扱うこととする。
〔分類方法と例〕
N個の点をK個(N未満)のクラスタに分類する方法を(1)～(5)に示す。
- N個の点(1からNまでの番号が付いている)からランダムにK個の点を選び(以下，初期設定という)，それらの点をコアと呼ぶ。コアには1からKまでのコア番号を付ける。なお，K個のコアの座標は全て異なっていなければならない。
- N個の点とK個のコアとの距離をそれぞれ計算し，各点から見て，距離が最も短いコア(複数存在する場合は，番号が最も小さいコア)を選ぶ。選ばれたコアのコア番号を，各点が所属する1回目のクラスタ番号(1からK)とする。ここで，二つの点をXY座標を用いてP＝(a，b)とQ＝(c，d)とした場合，PとQの距離を(a－c)2＋(b－d)2で計算する。
- K個のクラスタのそれぞれについて，クラスタに含まれる全ての点を使って重心を求める。ここで，重心のX座標をクラスタに含まれる点のX座標の平均，Y座標をクラスタに含まれる点のY座標の平均と定義する。ここで求めた重心の番号はクラスタの番号と同じとする。
- N個の点と各クラスタの重心(G1，…，GK)との距離をそれぞれ計算し，各点から見て距離が最も短い重心(複数存在する場合は，番号が最も小さい重心)を選ぶ。選ばれた重心の番号を，各点が所属する次のクラスタ番号とする。
- 重心の座標が変わらなくなるまで，(3)と(4)を繰り返す。
P1＝(1，0) P2＝(2，1) P3＝(4，1) P4＝(1.5，2) P5＝(1，3) P6＝(2，3) P7＝(4，3)
この手法のプログラムを図2に，プログラムで使う主な変数，関数及び配列を表3に示す。ここで，配列の添字は全て1から始まり，要素の初期値は全て0とする。
このアルゴリズムの最終結果は初期設定に依存し，そこでのコア間の距離が短いと適切な分類結果を得にくい。そこで，関数 initial において一つ目のコアはランダムに選び，それ以降はコア間の距離が長くなる点が選ばれやすくなるアルゴリズムを検討した。検討したアルゴリズムでは，t番目までのコアが決まった後，t＋1番目のコアを残った点から選ぶときに，それまでに決まったコアから離れた点を，より高い確率で選ぶようにする。具体的には，それまでに決まったコア(コア1～コアt)と，残ったN－t個の点から選んだ点Psとの距離の和をTsとする。N－t個の全ての点についてTsを求め，Tsがカほど高い確率で点Psが選ばれるようにする。このとき，点Psがt＋1番目のコアとして選ばれる確率としてキを適用する。
設問1
〔分類方法と例〕について，(1)，(2)に答えよ。
- 図1中のアに入れる座標を答えよ。
- 図1中の下線①のように分類が完了したときに，P1と同じクラスタに入る点を全て答えよ。
解答入力欄
- ア：
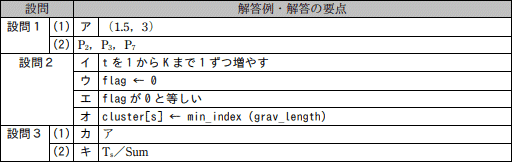
解答例・解答の要点
- ア：(1.5，3)
- P2，P3，P7
解説
- 〔アについて〕
クラスタ2の重心G2の座標が入ります。
重心の求め方は、問題文の〔分類方法と例〕(3)に「重心のX座標をクラスタに含まれる点のX座標の平均、Y座標をクラスタに含まれる点のY座標の平均と定義する。ここで求めた重心の番号はクラスタの番号と同じとする」と説明されています。
クラスタ2に含まれる点は、表1の所属クラスタ番号よりP5とP6であることがわかるので、P5とP6についてX座標とY座標の平均値を求めます。P5＝(1, 3)、P6＝(2, 3) ですから、- 重心G2のX座標 (1＋2)÷2＝1.5
- 重心G2のY座標 (3＋3)÷2＝3
∴ア＝(1.5, 3) - 重心の座標が変わらなくなるまで、(3)クラスタに含まれる点で重心を求める、(4)新たな重心を基準にクラスタを再構成する、という手順を繰り返します。
表2は手順(4)で所属クラスタの見直しが終了した時点の状態なので、手順(3)に戻りクラスタごとの重心を求めることから始めます。
クラスタ1に含まれる点は、P1、P2、P3およびP7なので、- 重心G1のX座標 (1＋2＋4＋4)÷4＝11／4＝2.75
- 重心G1のY座標 (0＋1＋1＋3)÷4＝5／4＝1.25
- 重心G2のX座標 (1.5＋1＋2)÷3＝4.5／3＝1.5
- 重心G2のY座標 (2＋3＋3)÷3＝8／3
次に重心と各点を距離を(a－c)2＋(b－d)2で計算するのですが、全部計算すると時間が掛かってしまうので、図1中のXYグラフに重心を打点して、各点との距離を見積もることになるでしょう。目分量で測った感じ、P1、P2およびP3は明らかにクラスタ1に、P4、P5およびP6は明らかにクラスタ2に所属することがわかると思います。P7については結構微妙ですが、地道に計算をするか定規等で距離を測ればクラスタ1に所属することが判断できるでしょう（定規が活躍する珍しい問です）。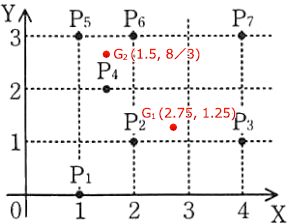
こうして分類されたクラスタは1回前（表2）のクラスタと変化ありません。所属クラスタに変化がない場合は重心の座標も変わらないため、これで分類が完了したことになります。したがって、分類が完了したときにP1と同じクラスに入る点は、「P2、P3、P7」の3つです。
∴P2，P3，P7
設問2
図2中のイ～オに入れる適切な字句を答えよ。
解答入力欄
- イ：
- ウ：
- エ：
- オ：
解答例・解答の要点
- イ：tを1からKまで1ずつ増やす
- ウ：flag←0
- エ：flagが0と等しい
- オ：cluster[s]←min_index(grav_length)
解説
〔イについて〕
ループ処理の繰返し条件が入ります。
ループ中で実行されている gravity_x と gravity_y はクラスタの重心のXY座標を求める関数、その結果を代入する coordinate_x と coordinate_y は各クラスタの重心のXY座標を格納する配列ですから、ここでは手順(3)の「K個のクラスタのそれぞれについて，クラスタに含まれる全ての点を使って重心を求める」を行っていることがわかります。
この処理はK個のクラスタのそれぞれについて行う必要があるため、クラスタ1～クラスタKまでの重心座標を配列の1～K個目に格納するように繰り返すことになります。ループ中では変数 t の値を変化させることによって各々の処理が行われるようになっています。本問のプログラムでは配列の添字は1から始まるので、繰返し条件としては「tを1からKまで1ずつ増やす」が当てはまります。
∴イ＝tを1からKまで1ずつ増やす
〔エについて〕
先にこちらから考えた方が分かりやすいので、[ウ]の前に[エ]に入る字句を考えます。
コメント部に「//終了して抜ける」とあるように、この条件式が真のときには return によりプログラムは終了することになります。プログラムを終了するのはクラスタが確定したとき、すなわち1回前と比較して重心が変わらなかったときですから、重心が変わっていないことを判断できる式が入ります。
[エ]の直前のブロックでは、重心の再設定が行われたときに flag に1をセットしています。このことから flag が1であれば1回前と比較して重心が変わっている、flag が1以外であれば変わっていないと言えます。表3を見ると flag の値は0又は1となっていますから、flagが1以外＝flagが0ということです。したがって、プログラムを終了する条件としては「flagが0と等しい」または「flagが1と等しくない」が適切となります。
∴エ＝flagが0と等しい
〔ウについて〕
前述のとおり、変数 flag は重心の再設定が行われたかどうかを表すためのフラグです。
クラスタ見直しの流れを見ると、
∴ウ＝flag←0
〔オについて〕
図2のプログラムの30～35行目の処理は、手順(4)の処理に対応します。ここでは、各点と再計算された各クラスタの重心との距離をそれぞれ計算し、各点から見て距離が最も短い重心の番号を、次の所属クラスタ番号にする処理を行います。
[オ]の直前のループ処理により、現在処理中の点Psにおける各クラスタの重心との距離は、配列 grav_length に格納されています。配列 grav_length 中で最も小さい値を持つ要素の添字が、次の所属クラスタ番号になります。配列 grav_length 中で最も小さい値を持つ要素の添字は、関数 min_index を使って、min_index(grav_length)で取得することが可能です。
その点がどのクラスタに所属するのかの情報は、配列 cluster に格納するので、min_index(grav_length) の結果を cluster[s] に代入することになります。したがって、空欄には「cluster[s]←min_index(grav_length)」が当てはまります。
∴オ＝cluster[s]←min_index(grav_length)
ループ処理の繰返し条件が入ります。
ループ中で実行されている gravity_x と gravity_y はクラスタの重心のXY座標を求める関数、その結果を代入する coordinate_x と coordinate_y は各クラスタの重心のXY座標を格納する配列ですから、ここでは手順(3)の「K個のクラスタのそれぞれについて，クラスタに含まれる全ての点を使って重心を求める」を行っていることがわかります。
この処理はK個のクラスタのそれぞれについて行う必要があるため、クラスタ1～クラスタKまでの重心座標を配列の1～K個目に格納するように繰り返すことになります。ループ中では変数 t の値を変化させることによって各々の処理が行われるようになっています。本問のプログラムでは配列の添字は1から始まるので、繰返し条件としては「tを1からKまで1ずつ増やす」が当てはまります。
∴イ＝tを1からKまで1ずつ増やす
〔エについて〕
先にこちらから考えた方が分かりやすいので、[ウ]の前に[エ]に入る字句を考えます。
コメント部に「//終了して抜ける」とあるように、この条件式が真のときには return によりプログラムは終了することになります。プログラムを終了するのはクラスタが確定したとき、すなわち1回前と比較して重心が変わらなかったときですから、重心が変わっていないことを判断できる式が入ります。
[エ]の直前のブロックでは、重心の再設定が行われたときに flag に1をセットしています。このことから flag が1であれば1回前と比較して重心が変わっている、flag が1以外であれば変わっていないと言えます。表3を見ると flag の値は0又は1となっていますから、flagが1以外＝flagが0ということです。したがって、プログラムを終了する条件としては「flagが0と等しい」または「flagが1と等しくない」が適切となります。
∴エ＝flagが0と等しい
〔ウについて〕
前述のとおり、変数 flag は重心の再設定が行われたかどうかを表すためのフラグです。
クラスタ見直しの流れを見ると、
- ウ
- 重心の再設定が行われた場合に flag を1にする
- flag が0であればプログラムを終了する
- 新しい重心でクラスタを再構成する
- 1.に戻る
∴ウ＝flag←0
〔オについて〕
図2のプログラムの30～35行目の処理は、手順(4)の処理に対応します。ここでは、各点と再計算された各クラスタの重心との距離をそれぞれ計算し、各点から見て距離が最も短い重心の番号を、次の所属クラスタ番号にする処理を行います。
[オ]の直前のループ処理により、現在処理中の点Psにおける各クラスタの重心との距離は、配列 grav_length に格納されています。配列 grav_length 中で最も小さい値を持つ要素の添字が、次の所属クラスタ番号になります。配列 grav_length 中で最も小さい値を持つ要素の添字は、関数 min_index を使って、min_index(grav_length)で取得することが可能です。
その点がどのクラスタに所属するのかの情報は、配列 cluster に格納するので、min_index(grav_length) の結果を cluster[s] に代入することになります。したがって、空欄には「cluster[s]←min_index(grav_length)」が当てはまります。
∴オ＝cluster[s]←min_index(grav_length)
設問3
〔初期設定の改良〕について，(1)，(2)に答えよ。
- 本文中のカに入れる適切な字句を解答群の中から選び，記号で答えよ。
- 本文中のキに入れる適切な式をTsとSumを使って答えよ。ここで，SumはN－t個の全てのTsの和とする。
カ に関する解答群
- 大きい
- 小さい
解答入力欄
- カ：
- キ：
解答例・解答の要点
- カ：ア
- キ：Ts／Sum
解説
- コアを選ぶ際、残った点のうち、それまでに決まったコアからの距離が長い点ほど選ばれやすくしたいのですから、距離が長い点ほど高い確率を与える必要があります。Tsはそれまでに決まった各コアと点Psとの距離の和ですから、距離が長いほどTsも大きくなります。したがって、Tsが大きいほど高い確率で選ばれるようにします。
∴カ＝大きい - TSはそれまでに決まった各コアと点Psの距離、Sumは残った点のTSの総和です。TSが大きいほど高い確率とするためには、Sum(全体)に対するTSの割合を選ばれる確率として使えばOKです。例えば、TSが10、20、30、40の4つの点（Sum＝100）があったとき、それぞれ10/100、20/100、30/100、40/100にすれば、ランダム性を保ちつつ、距離が長い点ほど選ばれやすくなるという感じです。
したがって、空欄には「Ts／Sum」が当てはまります。
∴キ＝Ts／Sum
