応用情報技術者過去問題 平成21年秋期 午後問2
⇄問題文と設問を画面2分割で開く⇱問題PDF問2 プログラミング
文字列照合処理に関する次の記述を読んで，設問1～3に答えよ。
ある文字列(テキスト)中で特定の文字列(パターン)が最初に一致する位置を求めることを文字列照合という。そのための方法として，次の二つを考える。ここで，テキストとパターンの長さは，どちらも1文字以上とする。
〔方法1 単純な照合方法〕
テキストを先頭から1文字ずつパターンと比較して，不一致の文字が現れたら，比較するテキストの位置(比較位置)を1文字分進める。この方法による処理例を図1に示す。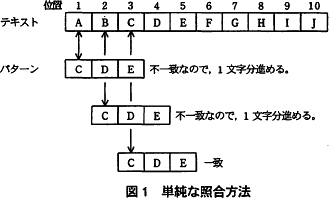
この手順を基に，テキストとパターンを与えると，最初に一致した文字位置を返すアルゴリズムを作成した。このアルゴリズムを図2に示す。
なお，テキストは配列 T，パターンは配列 P に格納されており，T[n] 及び P[n] はそれぞれのn番目の文字を，T.length 及び P.length はそれぞれの長さを示す。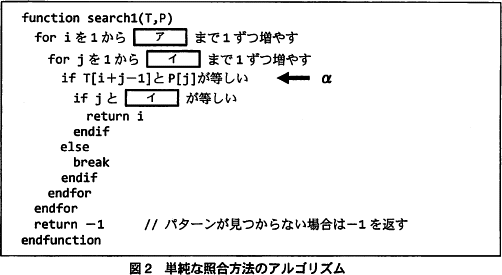
〔方法2 効率的な照合方法〕
方法1では，パターンとテキストの文字が不一致となった場合，比較位置を1文字分進めている。ここでは，比較位置をなるべく多くの文字数分進めることで，照合における比較回数を減らすことを考える。
パターンの末尾に対応する位置にあるテキストの文字(判定文字)に着目すると，次のように比較位置を進める文字数(スキップ数)が決定できる。
この方法による処理例を図3に示す。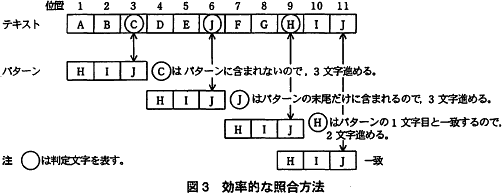
パターンが与えられると，判定文字に対応するスキップ数を一意に決定することができる。例えば，パターン HIJ に対して判定文字とスキップ数の対応表を作成すると表1のようになる。
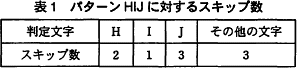この考え方を基に作成したアルゴリズムを図4に示す。
なお，テキストは配列 T，パターンは配列 P，スキップ数を決める表の判定文字は配列 C，スキップ数は配列 D に格納されており，T[n]，P[n]，C[n]，D[n] はそれぞれのn番目の文字又は数値を，T.length 及び P.length はテキストとパターンの長さを示す。
このアルゴリズムは，三つの主要部分から成っている。一つ目は，与えられたパターンについて判定文字とスキップ数の対応表を作成する処理である。ここでは，配列 C に格納される空白文字は表1の"その他の文字"及びパターンの末尾の文字"J"を表現するために使用している。テキストとパターンは空白文字を含まないものとする。二つ目は，文字を比較する処理である。ここでは，現在の比較位置に対応したテキストとパターンを方法1と同様に1文字ずつ比較して，パターンに含まれる文字と対応するテキストの文字がすべて一致するか，不一致となる文字が見つかるまで繰り返す。三つ目は，判定文字とスキップ数の対応表を引いてスキップ数を決定する処理である。
ある文字列(テキスト)中で特定の文字列(パターン)が最初に一致する位置を求めることを文字列照合という。そのための方法として，次の二つを考える。ここで，テキストとパターンの長さは，どちらも1文字以上とする。
〔方法1 単純な照合方法〕
テキストを先頭から1文字ずつパターンと比較して，不一致の文字が現れたら，比較するテキストの位置(比較位置)を1文字分進める。この方法による処理例を図1に示す。
なお，テキストは配列 T，パターンは配列 P に格納されており，T[n] 及び P[n] はそれぞれのn番目の文字を，T.length 及び P.length はそれぞれの長さを示す。
方法1では，パターンとテキストの文字が不一致となった場合，比較位置を1文字分進めている。ここでは，比較位置をなるべく多くの文字数分進めることで，照合における比較回数を減らすことを考える。
パターンの末尾に対応する位置にあるテキストの文字(判定文字)に着目すると，次のように比較位置を進める文字数(スキップ数)が決定できる。
- 判定文字がパターンに含まれていない場合は，判定文字とパターン内の文字の比較は常に不一致となるので，パターンの文字数分だけ比較位置を進める。また，判定文字がパターンの末尾だけに含まれている場合も，同様にパターンの文字数分だけ比較位置を進める。
- 判定文字がパターンの末尾以外に含まれている場合は，判定文字と一致するパターン内の文字が，テキストの判定文字に対応する位置に来るように比較位置を進める。ただし，パターン内に判定文字と一致する文字が複数ある場合は，パターンの末尾から最も近く(ただし，末尾を除く)にある判定文字と一致するパターン内の文字が，判定文字に対応する位置に来るように比較位置を進める。
この方法による処理例を図3に示す。
なお，テキストは配列 T，パターンは配列 P，スキップ数を決める表の判定文字は配列 C，スキップ数は配列 D に格納されており，T[n]，P[n]，C[n]，D[n] はそれぞれのn番目の文字又は数値を，T.length 及び P.length はテキストとパターンの長さを示す。
このアルゴリズムは，三つの主要部分から成っている。一つ目は，与えられたパターンについて判定文字とスキップ数の対応表を作成する処理である。ここでは，配列 C に格納される空白文字は表1の"その他の文字"及びパターンの末尾の文字"J"を表現するために使用している。テキストとパターンは空白文字を含まないものとする。二つ目は，文字を比較する処理である。ここでは，現在の比較位置に対応したテキストとパターンを方法1と同様に1文字ずつ比較して，パターンに含まれる文字と対応するテキストの文字がすべて一致するか，不一致となる文字が見つかるまで繰り返す。三つ目は，判定文字とスキップ数の対応表を引いてスキップ数を決定する処理である。
設問1
図2及び図4中のア～ウに入れる適切な字句を答えよ。
解答入力欄
- ア：
- イ：
- ウ：
解答例・解答の要点
- ア：T.length－P.Length＋1
- イ：P.Length
- ウ：P.Length－j
解説
〔アについて〕
解説の便宜上、図2のプログラムに行番号を振っておきます。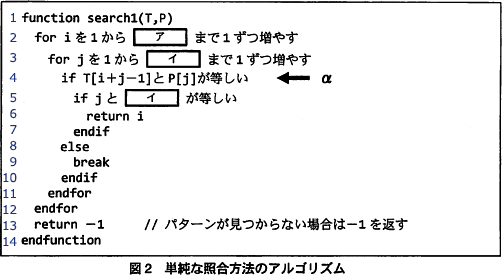
外側のforループにおける変数iの最終値です。
この関数は最初に一致した文字位置を返すこと、9行目で変数iが関数の返却値になっていることから、変数iはテキスト内の比較位置（比較を開始する位置）であることがわかります。
テキストの比較位置は1から始まり、パターンと一致しなければ1文字進めます。変数iが最大になるのがどのような場合かを考えると、下図のようにパターンの末尾位置がテキストの末尾位置と同じ場合になります。これ以上 i を進めても一致することはないため、この比較位置で一致しなければ照合処理を打ち切ることになるからです。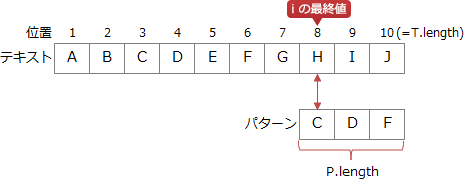
上図において、T.lengthが10、P.lengthが3のとき、iの最終値は3になりますから、これをT.length及びP.lengthを使って一般化すると「10－3＋1＝8」→「T.length－P.length＋1＝i」という関係に行き着きます。したがって、変数iの最終値を表す[ア]には「T.length－P.length＋1」が当てはまります。
∴ア＝T.length－P.Length＋1
〔イについて〕
内側のforループにおける変数jの最終値です。
図1の"CDE"を例に出すと、テキスト中の比較位置の文字と"C"(=P[1])を比較し、比較位置+1の位置の文字と"D"(=P[2])を比較し、比較位置+2の位置の文字と"E"(=P[3])を比較することになります。パターンの文字位置を1から P.length まで増やしながら処理を繰り返すので、変数jの最終値は「P.length」になります。
また、5～6行目に着目してみると、変数jが[イ]と等しいときは変数iの値を返して関数が終了していますから、[イ]にはパターンと一致したかどうかを判定するための式が入ります。
テキストとパターンが一致したことがわかるのは、パターンの末尾の文字との比較が終了した直後です。図1の"CDE"を例に出すと、"C"が一致し、"D"が一致し、"E"が一致したとき、つまり P.length 回一致したときにパターンが見つかったことになりますから、jの値が「P.length」であれば、テキスト中にパターンが見つかったと判断することができます。
∴イ＝P.length
〔ウについて〕
解説の便宜上、図4のプログラムの前半部分に行番号を振っておきます。
図4中のコメント「//(1):表の作成」で示されている部分は、「与えられたパターンについて判定文字とスキップ数の対応表を作成する処理」です。また、配列Pはパターン、配列Cはスキップ数を決める表の判定文字、配列Dはスキップ数を、それぞれ格納したものです。
10行目を見ると、スキップ数の表の判定文字 C[k] にパターンの文字 P[j] を代入していることから、11行目でスキップ数 D[k] に代入するのは、文字 P[j] に対応するスキップ数ということがわかります。
スキップ数の決定方法ですが、問題文中に「判定文字と一致するパターン内の文字が，テキストの判定文字に対応する位置に来るように比較位置を進める」とあります。ここでいう「テキストの判定文字に対応する位置」とは、図3より「パターンの末尾」を示します。したがって、スキップ数 D[k] に代入するのは、P[j] の文字をパターンの末尾の位置に進めるための移動数になります。この移動数とは、パターンの文字 P[j] とパターンの末尾との距離と考えればOKです。
表1の対応表で1番目の文字が2、2番目の文字が1となっているように、パターンの長さが P.length のとき、j番目の文字に対応するスキップ数は「P.length - j」と表すことができます。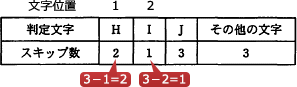
したがって[ウ]には「P.length - j」が当てはまります。
∴ウ＝P.Length－j
解説の便宜上、図2のプログラムに行番号を振っておきます。
この関数は最初に一致した文字位置を返すこと、9行目で変数iが関数の返却値になっていることから、変数iはテキスト内の比較位置（比較を開始する位置）であることがわかります。
テキストの比較位置は1から始まり、パターンと一致しなければ1文字進めます。変数iが最大になるのがどのような場合かを考えると、下図のようにパターンの末尾位置がテキストの末尾位置と同じ場合になります。これ以上 i を進めても一致することはないため、この比較位置で一致しなければ照合処理を打ち切ることになるからです。
∴ア＝T.length－P.Length＋1
〔イについて〕
内側のforループにおける変数jの最終値です。
図1の"CDE"を例に出すと、テキスト中の比較位置の文字と"C"(=P[1])を比較し、比較位置+1の位置の文字と"D"(=P[2])を比較し、比較位置+2の位置の文字と"E"(=P[3])を比較することになります。パターンの文字位置を1から P.length まで増やしながら処理を繰り返すので、変数jの最終値は「P.length」になります。
また、5～6行目に着目してみると、変数jが[イ]と等しいときは変数iの値を返して関数が終了していますから、[イ]にはパターンと一致したかどうかを判定するための式が入ります。
テキストとパターンが一致したことがわかるのは、パターンの末尾の文字との比較が終了した直後です。図1の"CDE"を例に出すと、"C"が一致し、"D"が一致し、"E"が一致したとき、つまり P.length 回一致したときにパターンが見つかったことになりますから、jの値が「P.length」であれば、テキスト中にパターンが見つかったと判断することができます。
∴イ＝P.length
〔ウについて〕
解説の便宜上、図4のプログラムの前半部分に行番号を振っておきます。
10行目を見ると、スキップ数の表の判定文字 C[k] にパターンの文字 P[j] を代入していることから、11行目でスキップ数 D[k] に代入するのは、文字 P[j] に対応するスキップ数ということがわかります。
スキップ数の決定方法ですが、問題文中に「判定文字と一致するパターン内の文字が，テキストの判定文字に対応する位置に来るように比較位置を進める」とあります。ここでいう「テキストの判定文字に対応する位置」とは、図3より「パターンの末尾」を示します。したがって、スキップ数 D[k] に代入するのは、P[j] の文字をパターンの末尾の位置に進めるための移動数になります。この移動数とは、パターンの文字 P[j] とパターンの末尾との距離と考えればOKです。
表1の対応表で1番目の文字が2、2番目の文字が1となっているように、パターンの長さが P.length のとき、j番目の文字に対応するスキップ数は「P.length - j」と表すことができます。
∴ウ＝P.Length－j
設問2
パターン HIPOPOTAMUS に対するスキップ数を表2に示す。エ，オに入れる適切な数値を答えよ。
解答入力欄
- エ：
- オ：
解答例・解答の要点
- エ：10
- オ：6
解説
次の2つの条件に注意してスキップ数を考えます。
〔エについて〕
パターン中に"H"は1つしかありません。パターン HIPOPOTAMUS は11文字(=P.length)であり、"H"は1番目の文字なので「11－1＝10」がスキップ数です。パターンの末尾から数えて10番目なので「10」と考えてもOKです。
〔オについて〕
パターン中に"P"は2つあります。末尾から近い方の"P"は5文字目の文字なので「11－5＝6」がスキップ数です。パターンの末尾から数えて6番目なので「6」と考えてもOKです。プログラム的な流れで言うと、j=3のとき D[3] が8に更新された後、j=5のとき再び D[3] は6に更新されることになります。
∴エ＝10
オ＝6
- スキップ数は末尾の文字との距離である
- パターン内に判定文字と一致する文字が複数ある場合は、パターンの末尾から最も近い文字で距離を判定する
〔エについて〕
パターン中に"H"は1つしかありません。パターン HIPOPOTAMUS は11文字(=P.length)であり、"H"は1番目の文字なので「11－1＝10」がスキップ数です。パターンの末尾から数えて10番目なので「10」と考えてもOKです。
パターン中に"P"は2つあります。末尾から近い方の"P"は5文字目の文字なので「11－5＝6」がスキップ数です。パターンの末尾から数えて6番目なので「6」と考えてもOKです。プログラム的な流れで言うと、j=3のとき D[3] が8に更新された後、j=5のとき再び D[3] は6に更新されることになります。
オ＝6
設問3
次のテキストとパターンに対して，図2でのαと図4でのβの実行回数をそれぞれ答えよ。
テキスト：PICKLED_PEPPER
パターン：PEP
テキスト：PICKLED_PEPPER
パターン：PEP
解答入力欄
- α：回
- β：回
解答例・解答の要点
- α：12
- β：8
解説
それぞれのアルゴリズムについてテキストとパターンの文字を比較する回数をカウントします。
〔αについて〕
∴α＝12回
〔βについて〕
はじめに、パターン PEP についてのスキップ数を考えておきます。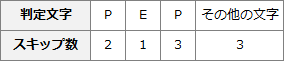
∴β＝8回
〔αについて〕
- PICとの比較で2回、1文字進める
- ICKとの比較で1回、1文字進める
- CKLとの比較で1回、1文字進める
- KLEとの比較で1回、1文字進める
- LEDとの比較で1回、1文字進める
- ED_との比較で1回、1文字進める
- D_Pとの比較で1回、1文字進める
- _PEとの比較で1回、1文字進める
- PEPとの比較で3回（終了）
∴α＝12回
〔βについて〕
はじめに、パターン PEP についてのスキップ数を考えておきます。
- PICとの比較で2回、判定文字Cはパターンに含まれないので3文字進める
- KLEとの比較で1回、判定文字Eはパターンの2文字目に含まれるので1文字進める
- LEDとの比較で1回、判定文字Dはパターンに含まれないので3文字進める
- _PEとの比較で1回、判定文字Eはパターンの2文字目に含まれるので1文字進める
- PEPとの比較で3回（終了）
∴β＝8回
