応用情報技術者過去問題 平成25年春期 午後問2
⇄問題文と設問を画面2分割で開く⇱問題PDF問2 プログラミング
一般的な表記法の数式を逆ポーランド表記法に変換するアルゴリズムに関する次の記述を読んで,設問1~3に答えよ。
逆ポーランド表記法とは,演算子を二つの演算対象の後ろに配置することによって,数式を表現する表記法である。例えば,一般的な表記法の数式 1+2×3 を,逆ポーランド表記法では 123×+ と表記する。
逆ポーランド表記法で表記した数式は,数値や演算子を左から順に処理すればよく,括弧を使う必要もないので,コンピュータが数式を取り扱うのに都合が良い。一般的な表記法の数式から逆ポーランド表記法への変換は,スタックを用いることで容易に実現できる。
〔逆ポーランド表記法への変換アルゴリズム〕
一般的な表記法の数式を逆ポーランド表記法に変換するアルゴリズムでは,まず変換前の数式を,数値,演算子及び括弧の要素(以下,演算要素という)に分解する。演算子には二項演算子+,-,×,÷を用い,括弧には"("と")"を用いる。数値は0~9の1桁の数とする。それぞれの演算要素には,優先度を定義する。
変換の処理には,変換前配列,スタック及び変換後配列を用いる。初期状態では,変換前配列には変換前の数式の演算要素が順に入っており,スタックと変換後配列は空の状態である。変換後には,変換後配列に逆ポーランド表記法に変換した結果が入る。例えば,変換前の数式が 1+2×3 の場合,初期状態は表1のようになる。 逆ポーランド表記法への変換は,次の(1)~(4)の手順で行う。
逆ポーランド表記法への変換は,次の(1)~(4)の手順で行う。
なお,図1中の丸で囲った演算要素は,(1)の手順で参照した演算要素である。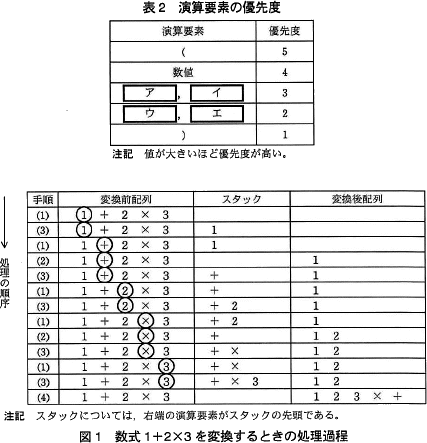 〔逆ポーランド表記法への変換プログラム〕
〔逆ポーランド表記法への変換プログラム〕
逆ポーランド表記法への変換プログラムを作成した。プログラム中で使用する主な変数,配列及び関数を表3に,作成したプログラムを図2に示す。
図2のプログラムでは,スタックの取扱いを容易にするために,ダミーの演算要素 null を定義し,プログラム開始直後にスタックにプッシュしている。
null がスタックからポップされることがないようにするために,その優先度をオと定義する。こうすることで,プログラム中,手順(2)の処理を行う部分でカの判定処理を記述する必要がなくなり,プログラムが簡潔になる。 〔エラーチェックの追加〕
〔エラーチェックの追加〕
図2のプログラムの①の箇所において,iが2以上のとき,GetElement(i-1) の優先度と,GetElement(i) の優先度を比較することによって,簡易的な入力エラーチェックを追加することができる。例えば,数値の演算要素が2個以上連続する場合や,")"の直後に"("が続く場合など,四則演算の式として不正なものがあった場合はエラーとする。
入力エラーとする条件を表4に示す。GetElement(i-1) の優先度と,GetElement(i) の優先度について,表4に従って評価をした結果,"OK"の場合は,そのまま処理を続行する。評価した結果が"Err"の場合は,入力された数式が誤っていると判断して処理を中断する。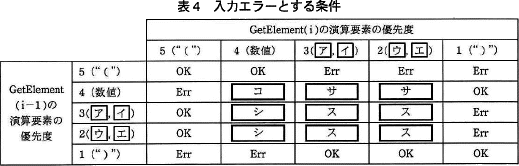
逆ポーランド表記法とは,演算子を二つの演算対象の後ろに配置することによって,数式を表現する表記法である。例えば,一般的な表記法の数式 1+2×3 を,逆ポーランド表記法では 123×+ と表記する。
逆ポーランド表記法で表記した数式は,数値や演算子を左から順に処理すればよく,括弧を使う必要もないので,コンピュータが数式を取り扱うのに都合が良い。一般的な表記法の数式から逆ポーランド表記法への変換は,スタックを用いることで容易に実現できる。
〔逆ポーランド表記法への変換アルゴリズム〕
一般的な表記法の数式を逆ポーランド表記法に変換するアルゴリズムでは,まず変換前の数式を,数値,演算子及び括弧の要素(以下,演算要素という)に分解する。演算子には二項演算子+,-,×,÷を用い,括弧には"("と")"を用いる。数値は0~9の1桁の数とする。それぞれの演算要素には,優先度を定義する。
変換の処理には,変換前配列,スタック及び変換後配列を用いる。初期状態では,変換前配列には変換前の数式の演算要素が順に入っており,スタックと変換後配列は空の状態である。変換後には,変換後配列に逆ポーランド表記法に変換した結果が入る。例えば,変換前の数式が 1+2×3 の場合,初期状態は表1のようになる。

- 変換前配列の先頭から順に,演算要素を1個参照する。
参照する演算要素がない場合は(4)に進む。 - スタック上に演算要素がある場合は,スタックの先頭にある演算要素の優先度を参照し,(1)の演算要素の優先度以上なら,スタックの先頭の演算要素をポップし,変換後配列の末尾に追加する。これを,スタックの先頭の演算要素の優先度が,(1)の演算要素の優先度未満になるまで繰り返す。ただし,スタックの先頭の演算要素が"("の場合は,そこで繰返しを終了する。
- (1)で参照した演算要素が")"なら,それを破棄し,その際スタックの先頭にあるはずの"("もポップして破棄した後(1)に戻る。(1)で参照した演算要素が")" 以外なら,その演算要素をスタックにプッシュし,(1)に戻る。
- スタック上にある全ての演算要素を順番にポップし,変換後配列の末尾に追加する。
なお,図1中の丸で囲った演算要素は,(1)の手順で参照した演算要素である。

逆ポーランド表記法への変換プログラムを作成した。プログラム中で使用する主な変数,配列及び関数を表3に,作成したプログラムを図2に示す。
図2のプログラムでは,スタックの取扱いを容易にするために,ダミーの演算要素 null を定義し,プログラム開始直後にスタックにプッシュしている。
null がスタックからポップされることがないようにするために,その優先度をオと定義する。こうすることで,プログラム中,手順(2)の処理を行う部分でカの判定処理を記述する必要がなくなり,プログラムが簡潔になる。

図2のプログラムの①の箇所において,iが2以上のとき,GetElement(i-1) の優先度と,GetElement(i) の優先度を比較することによって,簡易的な入力エラーチェックを追加することができる。例えば,数値の演算要素が2個以上連続する場合や,")"の直後に"("が続く場合など,四則演算の式として不正なものがあった場合はエラーとする。
入力エラーとする条件を表4に示す。GetElement(i-1) の優先度と,GetElement(i) の優先度について,表4に従って評価をした結果,"OK"の場合は,そのまま処理を続行する。評価した結果が"Err"の場合は,入力された数式が誤っていると判断して処理を中断する。

設問1
逆ポーランド表記法への変換について,(1),(2)に答えよ。
- 数式 (2+3)×4 を逆ポーランド表記法に変換した結果を答えよ。
- 表2及び表4中のア~エに入れる適切な二項演算子を,+,-,×,÷の中から一つずつ選んで,表を完成させよ。
解答入力欄
- ア:
- イ:
- ウ:
- エ:
解答例・解答の要点
- 23+4×
- ア:×
- イ:÷
- ウ:+
- エ:-
解説
- 問題文の冒頭部で「逆ポーランド表記法とは、演算子を二つの演算対象の後ろに配置することによって、数式を表現する表記法である」と説明されている通り、通常の数式「A+B」を逆ポーランド表記法で表現すると「AB+」になります。この変換規則に加えて、1回使った演算子は2度使わないことに注意して、普通に計算式を解くのと同じ順序で変換を行っていくことで逆ポーランド表記法の式になります。
数式 (2+3)×4 は以下のように変換されます。- 先に計算する"2+3"の部分を"変換する。
演算対象の"2"と"3"の後ろに"+"が配置されるので→23+×4 - "23+"を1つの項とみなして、演算子×、もう一つの項を4として変換する。
演算対象の"23×"と"4"の後ろに"×"が配置されるので→23+4×
∴23+4× - 先に計算する"2+3"の部分を"変換する。
- 逆ポーランドへの変換手順(2)において、スタックの先頭の演算要素の優先度が、参照中である変換前配列の要素の優先度未満になるまで、スタックからのポップ(取り出し操作)を繰り返すという操作手順に注目します。
図1の処理過程で"×"が参照されている時の操作を見ると、"2"はポップされ"+"はポップされていないことがわかります。つまり、"×"の優先度は"2"と同じかそれより低く、"+"より高いということです。演算の性質から考えて、"×"と"÷"、"+"と"-"は同じ優先度のグループとすべきなので、優先度が高い[ア][イ]には"×"と"÷"が、[ウ][エ]には"+"と"-"が当てはまります。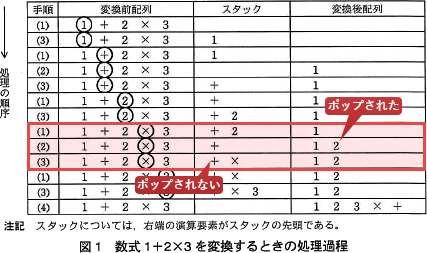
∴ア、イ=×、÷
ウ、エ=+、-
設問2
〔逆ポーランド表記法への変換プログラム〕について,(1)~(3)に答えよ。
- 本文中のオに入れる適切な数値を答えよ。
- 本文中のカに入れる適切な字句を20字以内で答えよ。
- 図2中のキ~ケに入れる適切な字句を答えよ。
解答入力欄
- オ:
- カ:
- キ:
- ク:
- ケ:
解答例・解答の要点
- オ:0
- カ:・スタック上に演算要素があるか否か (16文字)
・スタックが空であるか否か (12文字)
- キ:stack[stackCount]
- ク:GetPriority(stackTop) が elementPriority 以上
- ケ:GetElement(i) が ")" である
解説
- プログラム開始直後にスタックにプッシュするダミーの演算子 null の優先度を何にするかを考える問題です。
問題文の〔逆ポーランド表記法への変換アルゴリズム〕の(2)には、以下の記述があります。
「スタック上に演算要素がある場合は、スタックの先頭にある演算要素の優先度を参照し、(1)の演算要素の優先度以上なら、スタックの先頭の演算要素をポップし、変換後配列の末尾に追加する」
すなわち null がポップされないようにするためには、他のどの要素よりも優先度が低くなっている必要があります。表3の関数 GetPriority の説明に「演算要素の優先度を表す非負の整数を返す」とあるので、null に設定する優先度は、表2中で最も低い優先度である1よりも小さい、かつ、非負の整数でなければなりません。よって「0」しかありません。
∴オ=0 - 〔カについて〕
手順(2)は次の4つの処理に分解できます。- スタック上に演算要素があるか否かを確認する
- スタックの先頭にある演算要素の優先度を参照する
- スタックの先頭にある演算要素の優先度が、現在参照している演算要素の優先度以上ならポップする(繰り返し)
- スタックの先頭にある演算要素が")"なら繰返しを終了する
∴スタック上に演算要素があるか否か
スタックが空であるか否か - 〔キについて〕
表3中には変数 stackTop の用途について説明がありませんが、続くwhile文の継続条件式内で「stackTop が"("以外の間繰り返す」とあるので、stackTop はスタックの先頭の演算要素を格納するための変数だということがわかります。表2の注記にあるように「最後に追加された演算要素がスタックの先頭」なので、stackTop には配列 stack[] の末尾要素を格納することになります。
配列 stack[] の添字は1始まりですので、スタックの要素数を保持する変数 stackCount を使えば配列の末尾要素を参照できます。よって、[キ]には「stack[stackCount]」が当てはまります。
∴キ=stack[stackCount]
〔クについて〕
内側のwhile文内ではスタックからポップし、変換後配列 result に追加する操作が行われています。これを行うのは手順(2)の「スタックの演算要素の優先度が、現在参照している演算要素の優先度以上」の間ですので、[キ]には"スタック先頭の演算要素の優先度"と"現在参照している演算要素の優先度"を比較する式が入ります。
スタックの先頭にある演算要素の優先度は、表3中の優先度を取得する関数 GetPriority を使って「GetPriority(stackTop)」で取得できます。そして、現在参照している演算要素の優先度は変数 elementPriority に格納されています。よって[ク]に入る式は、「GetPriority(stackTop) が elementPriority 以上」が適切です。手順(2)の説明とは逆になりますが「elementPriority が GetPriority(stackTop) より小さい」でもプログラムの動作上は問題ないはずです。
∴ク=GetPriority(stackTop) が elementPriority 以上
〔ケについて〕
コメント「// 変換前配列を参照し,演算要素を処理する」直後のIF文は、以下の変換アルゴリズムの手順(3)に該当する処理です。
「(1)で参照した演算要素が")"なら,それを破棄し,その際スタックの先頭にあるはずの"("もポップして破棄した後(1)に戻る。(1)で参照した演算要素が")" 以外なら,その演算要素をスタックにプッシュし,(1)に戻る」
プログラムを見ると、[ケ]の式が真となる場合には stackCount の値をデクリメント(1減算)することでスタックの先頭(stack[] の末尾)にある要素"("を破棄し、偽である場合にはスタックに演算要素をプッシュしています。したがって[ケ]には、現在参照している演算要素が")"である旨の条件式が入ると判断できます。
変換前配列の演算要素は関数 GetElement で取得できるので、現在参照している i 番目の要素を参照するには「GetElement(i)」と記述することになります。この値が")"のとき真となれば良いので、[ケ]には「GetElement(i) が ")" である」が当てはまります。別の年度の午後問題では○と●が同一という字句表現も見られますので、「GetElement(i) と ")" が同一である」でも問題ないでしょう。
∴ケ=GetElement(i) が ")" である
設問3
表4中のコ~スに入れる適切な字句を答えよ。
解答入力欄
- コ:
- サ:
- シ:
- ス:
解答例・解答の要点
- コ:Err
- サ:OK
- シ:OK
- ス:Err
解説
〔コについて〕
数値の後に数値が現れる場合です。
〔逆ポーランド表記法への変換アルゴリズム〕で説明されているように、本アルゴリズムでは「数値は0~9の1桁の数」と限定しています。〔エラーチェックの追加〕にはエラーとする例として「数値の演算要素が2個以上連続する場合」とあるので、評価結果は「Err」です。
〔サについて〕
数値の後に演算子が現れる場合です。例えば「6÷」「1+」のようなケースがこれに該当します。これは一般的な表記法の数式として正しいため、評価結果は「OK」です。
〔シについて〕
[サ]とは逆に、演算子の後に数値が現れる場合です。例えば「÷6」「+1」のようなケースがこれに該当します。これは一般的な表記法の数式として正しいため、評価結果は「OK」です。
〔スについて〕
演算子の後に演算子が現れる場合です。例えば「÷+」「××」のようなケースがこれに該当します。これは一般的な表記法の数式として正しくないため、評価結果は「Err」です。
∴コ=Err
サ=OK
シ=OK
ス=Err
数値の後に数値が現れる場合です。
〔逆ポーランド表記法への変換アルゴリズム〕で説明されているように、本アルゴリズムでは「数値は0~9の1桁の数」と限定しています。〔エラーチェックの追加〕にはエラーとする例として「数値の演算要素が2個以上連続する場合」とあるので、評価結果は「Err」です。
〔サについて〕
数値の後に演算子が現れる場合です。例えば「6÷」「1+」のようなケースがこれに該当します。これは一般的な表記法の数式として正しいため、評価結果は「OK」です。
〔シについて〕
[サ]とは逆に、演算子の後に数値が現れる場合です。例えば「÷6」「+1」のようなケースがこれに該当します。これは一般的な表記法の数式として正しいため、評価結果は「OK」です。
〔スについて〕
演算子の後に演算子が現れる場合です。例えば「÷+」「××」のようなケースがこれに該当します。これは一般的な表記法の数式として正しくないため、評価結果は「Err」です。
∴コ=Err
サ=OK
シ=OK
ス=Err

