応用情報技術者過去問題 平成27年春期 午後問3
⇄問題文と設問を画面2分割で開く⇱問題PDF問3 プログラミング
データ圧縮の前処理として用いられるBlock-sortingに関する次の記述を読んで，設問1～4に答えよ。
Block-sortingは，文字列に対する可逆変換の一種である。変換後の文字列は，変換前の文字列と比較して同じ文字が多く続く傾向があるので，その後に行う圧縮処理において圧縮率を向上させることができる。
Block-sortingは，変換処理と復元処理の二つの処理で構成される。変換処理は，入力文字列を受け取って，変換結果の文字列と，入力文字列がソート後のブロックで何行目にあるか(以下，入力文字列の行番号という)を出力する。一方，復元処理は，変換結果の文字列と入力文字列の行番号を受け取って入力文字列を出力する。データ圧縮におけるBlock-sortingの使用方法を図1に示す。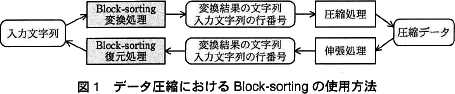
〔Block-sortingの変換処理〕
例として"papaya" を入力文字列としたときの変換処理を図2に示す。図2では，入力文字列を1文字左に巡回シフトすること(①)で文字列"apayap" となる。さらに，もう1文字左に巡回シフトすること(②)で文字列"payapa" となる。同様に1文字ずつ左に巡回シフトした(③～⑤)結果の文字列を縦に並べて正方形のブロック(巡回シフト後のブロック)を作成する。
次に，このブロックを行単位で辞書式順にソートし(⑥)，ソート後のブロックを得る。ソート後のブロックの各行の文字列から一番右の文字を行の順に取り出して並べた文字列と，ソート後のブロックにおいて入力文字列に一致する行の行番号を変換結果とする(⑦)。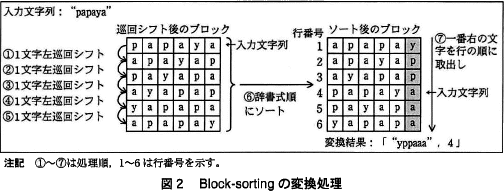
〔Block-sortingの復元処理〕
図2の変換結果「"yppaaa"，4」を復元する手順を表1に示す。
〔Block-sortingの実装〕
Block-sortingのプログラムを作成するために使用する配列，関数及び変数を，表2に示す。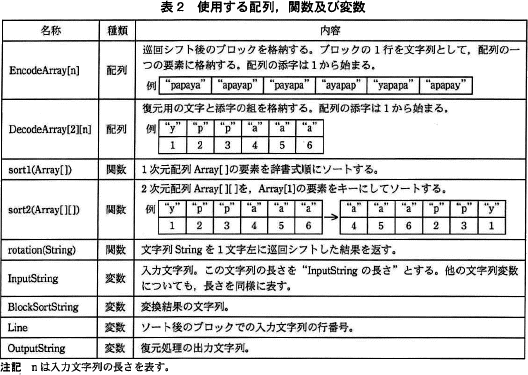
〔変換処理関数 encode〕
変換処理を実装した関数 encode のプログラムを図3に示す。
〔復元処理関数 decode〕
復元処理を実装した関数 decode のプログラムを図4に示す。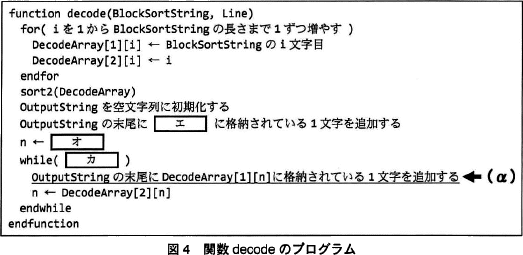
〔関数 sort2(Array[][])の実装〕
関数 decode の処理時間は，使用する関数 sort2(Array[][])の計算量に大きく依存する。処理時間を短くするためには，sort2(Array[][])の内部で計算量が少ないソートのアルゴリズムを使用して実装する必要がある。
処理時間の違いを確認するために複数のソートアルコリズムを使用して関数 sort2(Array[][])を実装したところ，Array[1]の要素をキーにしてクイックソート(不安定なソート)を使用した場合には復元処理の結果が入力文字列と一致しなかった。
この場合，sort2(Array[][])が表1の手順2を正しく実装できていないので，(β)ソートアルゴリズム，ソートキーのいずれかを見直す必要がある。
Block-sortingは，文字列に対する可逆変換の一種である。変換後の文字列は，変換前の文字列と比較して同じ文字が多く続く傾向があるので，その後に行う圧縮処理において圧縮率を向上させることができる。
Block-sortingは，変換処理と復元処理の二つの処理で構成される。変換処理は，入力文字列を受け取って，変換結果の文字列と，入力文字列がソート後のブロックで何行目にあるか(以下，入力文字列の行番号という)を出力する。一方，復元処理は，変換結果の文字列と入力文字列の行番号を受け取って入力文字列を出力する。データ圧縮におけるBlock-sortingの使用方法を図1に示す。
例として"papaya" を入力文字列としたときの変換処理を図2に示す。図2では，入力文字列を1文字左に巡回シフトすること(①)で文字列"apayap" となる。さらに，もう1文字左に巡回シフトすること(②)で文字列"payapa" となる。同様に1文字ずつ左に巡回シフトした(③～⑤)結果の文字列を縦に並べて正方形のブロック(巡回シフト後のブロック)を作成する。
次に，このブロックを行単位で辞書式順にソートし(⑥)，ソート後のブロックを得る。ソート後のブロックの各行の文字列から一番右の文字を行の順に取り出して並べた文字列と，ソート後のブロックにおいて入力文字列に一致する行の行番号を変換結果とする(⑦)。
図2の変換結果「"yppaaa"，4」を復元する手順を表1に示す。
Block-sortingのプログラムを作成するために使用する配列，関数及び変数を，表2に示す。
変換処理を実装した関数 encode のプログラムを図3に示す。
復元処理を実装した関数 decode のプログラムを図4に示す。
関数 decode の処理時間は，使用する関数 sort2(Array[][])の計算量に大きく依存する。処理時間を短くするためには，sort2(Array[][])の内部で計算量が少ないソートのアルゴリズムを使用して実装する必要がある。
処理時間の違いを確認するために複数のソートアルコリズムを使用して関数 sort2(Array[][])を実装したところ，Array[1]の要素をキーにしてクイックソート(不安定なソート)を使用した場合には復元処理の結果が入力文字列と一致しなかった。
この場合，sort2(Array[][])が表1の手順2を正しく実装できていないので，(β)ソートアルゴリズム，ソートキーのいずれかを見直す必要がある。
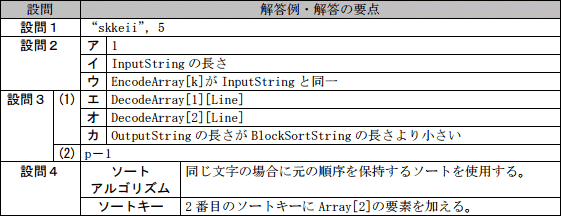
設問1
文字列"kiseki"に対してBlock-sortingを適用して変換した結果を答えよ。変換結果は図2の記法に合わせて記述すること。
解答入力欄
- o：
解答例・解答の要点
- o："skkeii"，5
解説
問題文の〔Block-sortingの変換処理〕に従い、入力文字列"kiseki"に対する変換結果を求めます。
まず、図2「Block-sortingの変換処理」にある「巡回シフト後のブロック」を求めるために、入力文字列"kiseki"を1文字左巡回シフトすることを入力文字数分だけ繰り返します。
末尾を並べた文字列は"skkeii"、入力文字列である"kiseki"は5行目に位置します。変換結果の記法は「"文字列", 行番号」なので、答えは「"skkeii", 5」となります。
∴"skkeii"，5
まず、図2「Block-sortingの変換処理」にある「巡回シフト後のブロック」を求めるために、入力文字列"kiseki"を1文字左巡回シフトすることを入力文字数分だけ繰り返します。
- 入力文字列："kiseki"
- (1回目)1文字左巡回シフト："isekik"
- (2回目)1文字左巡回シフト："sekiki"
- (3回目)1文字左巡回シフト："ekikis"
- (4回目)1文字左巡回シフト："kikise"
- (5回目)1文字左巡回シフト："ikisek"
- "ekikis"
- "ikisek"
- "isekik"
- "kikise"
- "kiseki"
- "sekiki"
末尾を並べた文字列は"skkeii"、入力文字列である"kiseki"は5行目に位置します。変換結果の記法は「"文字列", 行番号」なので、答えは「"skkeii", 5」となります。
∴"skkeii"，5
設問2
図3中のア～ウに入れる適切な字句を答えよ。
解答入力欄
- ア：
- イ：
- ウ：
解答例・解答の要点
- ア：1
- イ：InputStringの長さ
- ウ：EncodeArray[k]がInputStringと同一
解説
Block-sortingの変換処理の説明文をもとに〔変換処理関数 encode〕に当てはまる字句を考えます。
〔ア、イについて〕
図3「関数 encode のプログラム」の4行目から5行目は、for文の中で行う処理です。この反復処理では、4行目で EncodeArray[i] に rString の文字列を代入し、5行目で rString の文字列を1文字左巡回シフトした文字列を rString に代入しています。つまり、この処理は巡回シフト後のブロックを作成する処理（図2中の①～⑤）に相当します。
図2の入力文字列が"papaya"の場合を見ると、正方形のブロックのデータは EncodeArray[1] から EncodeArray[6] に格納されています。つまり、入力文字列をもとに正方形のブロックを作成するためには、EncodeArray[] への代入と1文字左巡回シフトを入力文字列の文字数と同じ回数だけ行う必要があるということです。
EncodeArray[] の添字は1から始まるので、iを1から入力文字列(InputString)の長さまで増やしながら反復することで正方形のブロックを表すデータが作成されることとなります。
∴ア＝1、イ＝InputStringの長さ
〔ウについて〕
問題文の図3「関数 encode のプログラム」の9行目から14行目の処理は、図2「Block-sortingの変換処理」の⑦に対応する処理です。
図3「関数encodeのプログラム」の12行目は、ループカウンタ変数であり行番号を示す k を変数 Line に代入しています。Line は、ソート後のブロックでの入力文字列の行番号を保持する変数です。
9行目から14行目の反復処理では、BlockSortStringの末尾にソート済みブロックの末尾を加える処理を行いながら、入力文字列と一致する行を探しています。Line に行番号を代入するのは、その行の文字列が入力文字列と同じときです。当該行の文字列は EncodeArray[k]、入力文字列は InputString で参照できるので、分岐条件式としてはEncodeArray[k]がInputStringと同一が適切となります。
∴ウ＝EncodeArray[k]がInputStringと同一
〔ア、イについて〕
図3「関数 encode のプログラム」の4行目から5行目は、for文の中で行う処理です。この反復処理では、4行目で EncodeArray[i] に rString の文字列を代入し、5行目で rString の文字列を1文字左巡回シフトした文字列を rString に代入しています。つまり、この処理は巡回シフト後のブロックを作成する処理（図2中の①～⑤）に相当します。
図2の入力文字列が"papaya"の場合を見ると、正方形のブロックのデータは EncodeArray[1] から EncodeArray[6] に格納されています。つまり、入力文字列をもとに正方形のブロックを作成するためには、EncodeArray[] への代入と1文字左巡回シフトを入力文字列の文字数と同じ回数だけ行う必要があるということです。
EncodeArray[] の添字は1から始まるので、iを1から入力文字列(InputString)の長さまで増やしながら反復することで正方形のブロックを表すデータが作成されることとなります。
∴ア＝1、イ＝InputStringの長さ
〔ウについて〕
問題文の図3「関数 encode のプログラム」の9行目から14行目の処理は、図2「Block-sortingの変換処理」の⑦に対応する処理です。
図3「関数encodeのプログラム」の12行目は、ループカウンタ変数であり行番号を示す k を変数 Line に代入しています。Line は、ソート後のブロックでの入力文字列の行番号を保持する変数です。
9行目から14行目の反復処理では、BlockSortStringの末尾にソート済みブロックの末尾を加える処理を行いながら、入力文字列と一致する行を探しています。Line に行番号を代入するのは、その行の文字列が入力文字列と同じときです。当該行の文字列は EncodeArray[k]、入力文字列は InputString で参照できるので、分岐条件式としてはEncodeArray[k]がInputStringと同一が適切となります。
∴ウ＝EncodeArray[k]がInputStringと同一
設問3
〔復元処理関数 decode〕について，(1)，(2)に答えよ。
- 図4中のエ～カに入れる適切な字句を答えよ。
- BlockSortStringの長さがpのとき，図4中の下線(α)の処理の実行回数を答えよ。
解答入力欄
- エ：
- オ：
- カ：
解答例・解答の要点
- エ：DecodeArray[1] [Line]
- オ：DecodeArray[2] [Line]
- カ：OutputStringの長さがBlockSortStringの長さより小さい
- p－1
解説
- 〔エについて〕
問題文の図4「関数decodeのプログラム」の7行目から13行目は、問題文の表1「Block-sortingの復号手順」の手順3に対応する処理です。
7行目では出力となる OutputString を空文字列で初期化していますから、8行目の処理で代入されるのは最初の1文字目ということになります。最初の文字は、ソート後の文字列から"変換結果の行番号"に位置する文字を取り出します。"変換結果の行番号"とは、関数 encode 内でLineに代入されている行番号です。
表2を見ると DecodeArray[] は多次元配列で、DecodeArray[1] は復元用の文字を、DecodeArray[2] は(元の)添字を保持しているので、OutputString の1文字目にはDecodeArray[1][Line]を代入するのが適切です。
∴エ＝DecodeArray[1][Line]
〔オについて〕
手順3を見ると、- Lineを基準に、Line番目の要素 p(2) を取り出して出力に追加
- p(2)の2を基準に、2番目の要素 a(5) を取り出して出力に追加
- a(5)の5を基準に、5番目の要素 p(3) を取り出して出力に追加
- …
∴オ＝DecodeArray[2][Line]
〔カについて〕
ループの継続条件が入ります。
手順3の最後に「以降、並べた要素の個数が変換結果の文字列の長さになるまで，要素を取り出して並べることを繰り返す」とあります。よって、ループ内の処理は、並べた要素の個数が変換結果の文字列の長さよりも小さい間反復する必要があります。並べた要素は OutputString、変換結果の文字列は引数の BlockSortString ですので、カにはOutputStringの長さがBlockSortStringの長さより小さいが入ります。
∴カ＝OutputStringの長さがBlockSortStringの長さより小さい - Block-sortingでは、InputString をもとに正方形のブロックを生成し、そこから変換後の文字列を取り出すので、InputString と BlockSortString の長さは同一になります。関数 decode は、BlockSortString を InputString に復元するのが目的ですので、関数終了時の OutputString の長さは、InputStringと同じ、すなわち BlockSortString と同じということに着目しましょう。
(α)では OutputString に所定の1文字を追加します。ループの開始前にエの行で1文字目を代入しているので、ループ処理では残りの文字数分だけ文字の追加を行わなくてはなりません。BlockSortString の長さが p であれば、(α)の処理は最初の1文字を除いたp－1回だけ実行されることとなります。
∴p－1
設問4
本文中の下線(β)について，ソートアルゴリズムを見直す場合とソートキーを見直す場合のそれぞれについて，どのように見直せばよいかを30字以内で述べよ。
解答入力欄
- ソートアルゴリズム：
- ソートキー：
解答例・解答の要点
- ソートアルゴリズム：
同じ文字の場合に元の順序を保持するソートを使用する (25文字) - ソートキー：2番目のソートキーにArray[2]の要素を加える (25文字)
解説
問題文中にクイックソート（不安定なソート）と記載されているように、クイックソートでは同じ文字があった場合に、ソート前の順序がソート後も保存されるとは限りません。Block-sortingの復元手順の手順2にあるように「文字をソートする。同じ文字の場合は添字の順に並べる」ことが条件となっているため、不安定なソートでは期待通りに動作しない（復元処理の結果が入力文字列と一致しない）ことがあります。
〔ソートアルゴリズムについて〕
不安定なソートとは逆に、ソート前の順序がソート後も保存される性質を持つソートアルゴリズムを安定なソート（stable sort）といいます。不安定なソートアルゴリズムを用いていることが原因なのですから、安定なソートアルゴリズムを使用するように変更すれば問題を解消できます。
よって、ソートアルゴリズムを見直す場合は、同じ文字の場合に元の順序を保持するソート（安定なソート）を使用するが適切です。
∴同じ文字の場合に元の順序を保持するソートを使用する
〔ソートキーについて〕
クイックソートのような不安定なソートを用いる場合でもキーの工夫によって問題を解消できます。クイックソートでは比較条件として複数のキーと指定することもできるので、1番目のソートキー（文字）が同じ場合は、2番目のソートキー（添字）の大小でソートすれば手順2の条件を満たすことができます。
よって、ソートキーを見直す場合は、2番目のソートキーにArray[2]の要素を加えるが適切です。あくまで憶測ですが、Array[1]の文字とArray[2]の添字を連結した文字列をキーに指定するとかでもいいのかもしれません。
∴2番目のソートキーにArray[2]の要素を加える
〔ソートアルゴリズムについて〕
不安定なソートとは逆に、ソート前の順序がソート後も保存される性質を持つソートアルゴリズムを安定なソート（stable sort）といいます。不安定なソートアルゴリズムを用いていることが原因なのですから、安定なソートアルゴリズムを使用するように変更すれば問題を解消できます。
よって、ソートアルゴリズムを見直す場合は、同じ文字の場合に元の順序を保持するソート（安定なソート）を使用するが適切です。
∴同じ文字の場合に元の順序を保持するソートを使用する
〔ソートキーについて〕
クイックソートのような不安定なソートを用いる場合でもキーの工夫によって問題を解消できます。クイックソートでは比較条件として複数のキーと指定することもできるので、1番目のソートキー（文字）が同じ場合は、2番目のソートキー（添字）の大小でソートすれば手順2の条件を満たすことができます。
よって、ソートキーを見直す場合は、2番目のソートキーにArray[2]の要素を加えるが適切です。あくまで憶測ですが、Array[1]の文字とArray[2]の添字を連結した文字列をキーに指定するとかでもいいのかもしれません。
∴2番目のソートキーにArray[2]の要素を加える
