応用情報技術者過去問題 平成28年秋期 午後問3
⇄問題文と設問を画面2分割で開く⇱問題PDF問3 プログラミング
魔方陣に関する次の記述を読んで，設問1～3に答えよ。
魔方陣とは，正方形のマス目(方陣)に数を配置し，縦・横・対角線のいずれにおいても，その並びの数の合計が同じになるものである。ここでは，N×Nの方陣(Nは3以上の自然数)に1からN2までの数を過不足なく配置したものとする。このとき，縦・横・対角線のN個のマスの合計値は，いずれも(ア＋N)÷2となる。
Nが3の場合の魔方陣の一つを図1に示す。
Nが奇数の場合，魔方陣の一つを次の手順で作ることができる。N＝3のときに，この手順によって1～6の数が配置される様子を図2に示す。
〔魔方陣の作り方〕
魔方陣の作り方は，次のとおりである。ここで(A)～(E)は図2中の該当箇所を示す。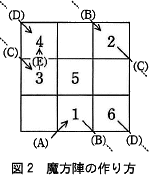
〔魔方陣のプログラム〕
魔方陣の数の配置を記憶する，整数型の2次元配列 houjin を用意する。配列の添字は1から始まる。行y列xのマスは，houjin[y][x] で表現する。例えば， 図1中の1が配置されているマスは，houjin[3][2] である。
数の配置に関する判定をするために，配列 houjin の領域を(N＋1)×(N＋1)の大きさで用意し，適切な初期値を設定する。Nが3の場合の例を図3に示す。数が既に配置されているかどうかを判定するために，図3の太枠内の各マスの初期値は0とする。また，現在位置の右下のマスが太枠の外であることを判定するために， 4行目のマスに SOTO_SHITA， 4列目のマスにSOTO_MIGI，行4列4のマスにSOTO_KADOの三つの異なる定数(0からN2までの整数以外の整数)を初期値として設定する。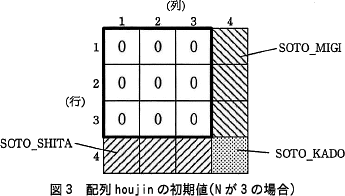
配列 houjin の初期化をする関数 shokika，及び数を配置する関数 mahoujin のプログラムを図4に示す。引数Nは，正の奇数(N≧3)である。
〔プログラムの判定部分の改変〕
図4のプログラムによるメモリ使用量の削減のために，配列 houjin の領域をN×Nに縮小し，定数SOTO_SHITA， SOTO_MIGI及びSOTO_KADOを使わないようにするプログラムの改変を考えた。図4の(F)の部分を改変したプログラムを図5に示す。
魔方陣とは，正方形のマス目(方陣)に数を配置し，縦・横・対角線のいずれにおいても，その並びの数の合計が同じになるものである。ここでは，N×Nの方陣(Nは3以上の自然数)に1からN2までの数を過不足なく配置したものとする。このとき，縦・横・対角線のN個のマスの合計値は，いずれも(ア＋N)÷2となる。
Nが3の場合の魔方陣の一つを図1に示す。
〔魔方陣の作り方〕
魔方陣の作り方は，次のとおりである。ここで(A)～(E)は図2中の該当箇所を示す。
- N×Nの全てのマスは何も入っていない空白の状態とする。
- 最下行の中央のマスを現在位置とし，現在位置に数1を配置する(A)。
- 現在位置の右下のマスが空白かどうか確認する。このとき，最下行の下は最上行(B)，最右列の右は最左列(C)とする。右下隅の右下は，左上隅(D)である。
- (3)で確認したマスが空白の場合は，そこを新しい現在位置とする。(3)で確認したマスが空白でない場合は，現在位置の上のマスを新しい現在位置とする(E)。この際，新しい現在位置が最上行よりも上になることはない。
- 数を一つ増やし，現在位置にその数を配置する。
- 全てのマスが埋まるまで， (3)～(5)を繰り返す。
魔方陣の数の配置を記憶する，整数型の2次元配列 houjin を用意する。配列の添字は1から始まる。行y列xのマスは，houjin[y][x] で表現する。例えば， 図1中の1が配置されているマスは，houjin[3][2] である。
数の配置に関する判定をするために，配列 houjin の領域を(N＋1)×(N＋1)の大きさで用意し，適切な初期値を設定する。Nが3の場合の例を図3に示す。数が既に配置されているかどうかを判定するために，図3の太枠内の各マスの初期値は0とする。また，現在位置の右下のマスが太枠の外であることを判定するために， 4行目のマスに SOTO_SHITA， 4列目のマスにSOTO_MIGI，行4列4のマスにSOTO_KADOの三つの異なる定数(0からN2までの整数以外の整数)を初期値として設定する。
図4のプログラムによるメモリ使用量の削減のために，配列 houjin の領域をN×Nに縮小し，定数SOTO_SHITA， SOTO_MIGI及びSOTO_KADOを使わないようにするプログラムの改変を考えた。図4の(F)の部分を改変したプログラムを図5に示す。
設問1
本文中のアに入れる適切な式を答えよ。
(※正誤判定の都合上、指数部を"^"で入力してください。Rの2乗→R^2)
(※正誤判定の都合上、指数部を"^"で入力してください。Rの2乗→R^2)
解答入力欄
- ア：
解答例・解答の要点
- ア：N3
解説
〔アについて〕
魔法陣に配置する数字は、1からN2までの数です。よって、配置した数の合計は、
1＋2＋…＋N2
となります。これは1からN2まで順に並んだ等差数列ですので、その総和は以下の式で求めることができます。
(1＋N2)×(N2／2)
魔法陣の横方向の行に着目した場合、すべての行の合計は等しいことになります。よって「1行の合計＝全体の合計÷行数」で求めることができます。3×3では「45÷3＝15」が1行の合計になります（45は1から9までの総和）。
すなわち、1行の合計は、
(1＋N2)×(N2／2)×1／N
＝{N2(1＋N2)}／2N
＝{N(1＋N2)}／2
＝(N＋N3)／2
となります。以上よりアにはN3が入ります。
また、図1の3×3の魔法陣の例を用いてアを求めることもできます。例えば、図1の魔法陣の1行目のマスの和は「4＋9＋2＝15」です。N＝3ですので、問題文中の式より「(ア＋3)÷2＝15」となることがわかります。よって、「ア＝15×2－3＝27」となります。
これだけでは、ア＝N3と断定できませんが、本文の手順に従って正の奇数である5×5の魔方陣を描いてみると「(ア＋5)÷2＝65」で、ア＝125 となります。N＝3のとき27、N＝5のとき125になるのでアにはN3が入ると判断できます。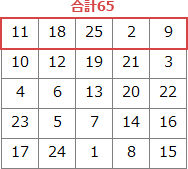
∴ア＝N3
魔法陣に配置する数字は、1からN2までの数です。よって、配置した数の合計は、
1＋2＋…＋N2
となります。これは1からN2まで順に並んだ等差数列ですので、その総和は以下の式で求めることができます。
(1＋N2)×(N2／2)
魔法陣の横方向の行に着目した場合、すべての行の合計は等しいことになります。よって「1行の合計＝全体の合計÷行数」で求めることができます。3×3では「45÷3＝15」が1行の合計になります（45は1から9までの総和）。
すなわち、1行の合計は、
(1＋N2)×(N2／2)×1／N
＝{N2(1＋N2)}／2N
＝{N(1＋N2)}／2
＝(N＋N3)／2
となります。以上よりアにはN3が入ります。
また、図1の3×3の魔法陣の例を用いてアを求めることもできます。例えば、図1の魔法陣の1行目のマスの和は「4＋9＋2＝15」です。N＝3ですので、問題文中の式より「(ア＋3)÷2＝15」となることがわかります。よって、「ア＝15×2－3＝27」となります。
これだけでは、ア＝N3と断定できませんが、本文の手順に従って正の奇数である5×5の魔方陣を描いてみると「(ア＋5)÷2＝65」で、ア＝125 となります。N＝3のとき27、N＝5のとき125になるのでアにはN3が入ると判断できます。
設問2
〔魔方陣のプログラム〕について，(1)，(2)に答えよ。
- 図4中のイ～キに入れる適切な字句を答えよ。
- 図4の関数 mahoujin を実行した場合，配列 houjin の中で一度も参照も代入もされない要素が二つ存在する。該当する配列 houjin の要素をそれぞれ答えよ。
解答入力欄
- イ：
- ウ：
- エ：
- オ：
- カ：
- キ：
- ①：
- ②：
解答例・解答の要点
- イ：houjin[y] [N＋1]
- ウ：houjin[N＋1] [x]
- エ：x←(N＋1)/2
- オ：N2未満
- カ：yb-1
- キ：xb
- ①：houjin[1] [N＋1]
- ②：houjin[N＋1] [1]
解説
- 〔イについて〕
SOTO_MIGIをどこに代入するかを問う問題です。問題文の図3より、N＝3の場合には、配列houjin[1][4]、houjin[2][4]、houjin[3][4]にSOTO_MIGIを代入することがわかります。これは、houjin[1][N+1]、houjin[2][N+1]、houjin[3][N+1]と表すことができます。
また、プログラムの2・3行目より、イの処理はN回実行され、そのときのy及びxの値は(y=1,x=N)、(y=2,x=N)、…、(y=N,x=N)であることがわかります。
よって、イにはhoujin[y][N+1]が入ります。
∴イ＝houjin[y][N+1]
〔ウについて〕
SOTO_SHITAをどこに代入するかを問う問題です。問題文の図3より、N＝3の場合には、配列houjin[4][1]、houjin[4][2]、houjin[4][3]にSOTO_SHITAを代入することがわかります。これは、houjin[N+1][1]、houjin[N+1][2]、houjin[N+1][3]と表すことができます。
また、プログラムの8行目より、xの値は1からNまで1ずつ増えることがわかります。
よって、ウにはhoujin[N+1][x]が適切です。
∴ウ＝houjin[N+1][x]
〔エについて〕
mahoujin の最初に行う処理であること、及び、1をhoujin[y][x]に代入していることから、問題文の〔魔法陣の作り方〕(2)の「最下行の中央のマスを現在位置とし、現在位置に数1を配置する(A)」に対応する処理とわかります。行を表す変数はy、列を表す変数はxです。最下行は単純に N 行目になります。中央列は N＝3のとき2、N＝5のとき3、N＝7のとき4ですので、これを返す式は (N＋1)/2 になります※。
よって、エにはx ← (N＋1)/2が入ります。
∴エ＝x ← (N+1)/2
※(N－1)/2＋1 でも大丈夫だと思います。
〔オについて〕
数を配置する処理を繰り返す条件が入ります。数の配置は魔法陣のマス(N2)だけ繰り返します。
mahoujin のループ処理の最後を見ると、suuji に1を加算した後に配列 houjin に代入しています。このことから、houjin に2からN2を設定するには、ループを1からN2-1まで繰り返す必要があります。つまり、suuji がN2になったら繰り返し処理が終わりになるような条件を指定しなければなりません。
よって、オにはN2未満が入ります。
〔カ、キについて〕
「houjin[y][x]が0と等しくない」場合に行う処理です。これは、問題文の〔魔法陣の作り方〕(4)の「…(3)で確認したマスが空白でない場合は、現在位置の上のマスを新しい現在位置とする(E)。…」に対応する処理です。すなわち、格納候補のマスに既に何らかの数字が格納されているときです。
mahoujin の6・7行目では yb,xb に現在位置の x,y を格納しています。現在位置の上のマスは、列はそのままで行が1だけ小さい位置ですので、yにはyb-1を、xにはxbを代入することになります。
∴カ＝yb-1
キ＝xb - 今回の魔法陣では、配列 houjin[1][1]～houjin[N][N] には必ず値を格納するので、これらの要素は参照・代入を行います。すなわち、参照・代入を行わない要素は、魔方陣の外側にある SOTO_xxxx が設定されているマスの中にあることがわかります。
そして〔魔法陣の作り方〕より、現在位置の右下の要素を参照・代入する候補とすることから、左上に位置する要素が houjin[1][1]～houjin[N][N] の中ではない要素が、参照・代入されない要素になります。これらの条件を満たす要素は、houjin[1][N+1] と houjin[N+1][1] です。∴①＝houjin[1][N+1]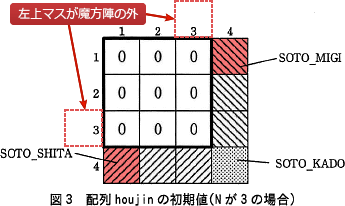
②＝houjin[N+1][1]
設問3
図5中のク，ケに入れる適切な字句を答えよ。
解答入力欄
- ク：
- ケ：
解答例・解答の要点
- ク：N
- ケ：1
解説
(F)の処理は、代入候補のマスが魔方陣の範囲外の場合に、「最下行の下は最上行、最右列の右は最左列、右下隅の右下は左上隅」の条件に従って、代入候補のマスを変更する処理です。図5の改変したプログラムは、これを同等の処理を行うものでなければなりません。
代入候補のマスが魔方陣の範囲外の場合ということは、yがNよりも大きい場合とxがNよりも大きい場合の処理であると言えます。yがNよりも大きくなった場合は、yを1に戻す必要があります。同様にxがNよりも大きくなった場合は、xを1に戻す必要があります。
よって、クにはN、ケには1が入ります。
∴ク＝N
ケ＝1
代入候補のマスが魔方陣の範囲外の場合ということは、yがNよりも大きい場合とxがNよりも大きい場合の処理であると言えます。yがNよりも大きくなった場合は、yを1に戻す必要があります。同様にxがNよりも大きくなった場合は、xを1に戻す必要があります。
よって、クにはN、ケには1が入ります。
∴ク＝N
ケ＝1
