応用情報技術者過去問題 令和2年秋期 午後問3
⇄問題文と設問を画面2分割で開く⇱問題PDF問3 プログラミング
誤差拡散法による減色処理に関する次の記述を読んで，設問1～4に答えよ。
画像の情報量を落として画像ファイルのサイズを小さくしたり，モノクロの液晶画面に画像を表示させたりする際に，減色アルゴリズムを用いた画像変換を行うことがある。誤差拡散法は減色アルゴリズムの一つである。誤差拡散法を用いて，階調ありのモノクロ画像を，黒と白だけを使ったモノクロ2値の画像に画像変換した例を図1に示す。
階調ありのモノクロ画像の場合は，各ピクセルが色の濃淡をもつことができる。濃淡は輝度で表す。輝度0のとき色は黒に，輝度が最大になると色は白になる。モノクロ2値の画像は，輝度が0か最大かの2値だけを使った画像である。
〔誤差拡散法のアルゴリズム〕
画像を構成するピクセルの輝度は，1ピクセルの輝度を8ビットで表す場合，0～255の値を取ることができる。0が黒で，255が白を表す。誤差拡散法では，次の二つの処理をピクセルごとに行うことで減色を行う。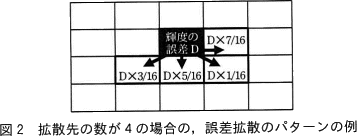
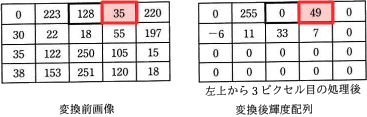
図2のパターンを使い，図3の手順に従って，1行目の左上から2ピクセル分の処理をした後，その右隣のピクセル(左上から3ピクセル目)について処理した例を図4に示す。変換前画像の輝度の値が128で，変換後輝度配列の同じ要素の値が－14なので，Fは128＋(－14)＝114となる。Fが128未満なので，輝度は0，誤差Dは114となる。誤差114に7/16を乗じて，小数点以下を切り捨てた値は49なので，変換後輝度配列の一つ右の要素に49を加算する。同様に，左下には21，下には35，右下には7を加算する。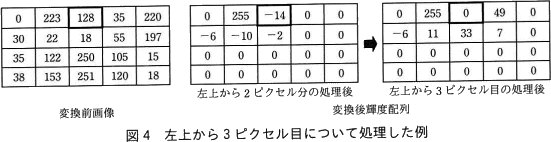
〔誤差拡散法を用いて減色するプログラム〕
誤差拡散法を用いて減色するプログラムを作成した。プログラム中で使用する主な変数，定数及び配列を表1に，作成したプログラムを図5に示す。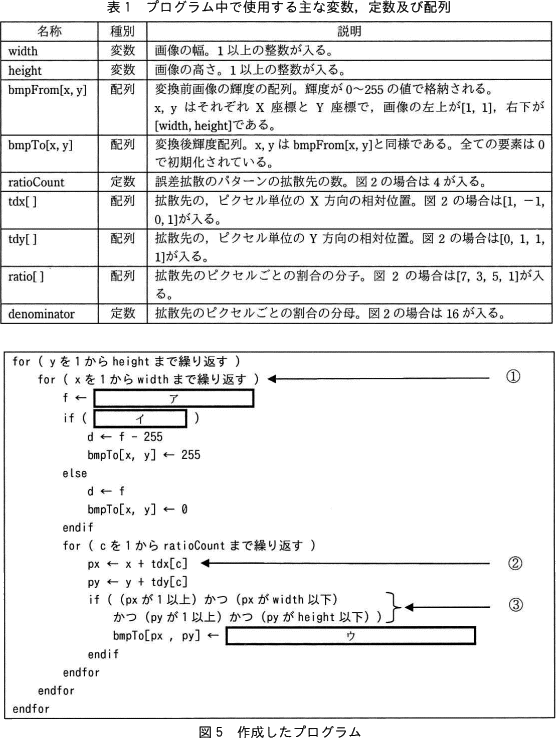
〔画質向上のための改修〕
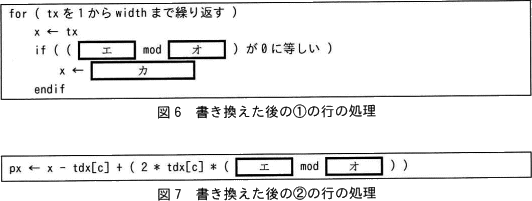
ピクセルを処理する順番を，Y座標ごとに逆向きにすることで，誤差拡散の方向の偏りを減らし，画質を改善することができる。
〔処理の高速化に関する検討〕
図5中の③の箇所では，誤差を拡散させる先のピクセルが画像の範囲の外側にならないように制御している。このような処理をクリッピングという。
③のif文は，プログラムの終了までにキ回呼び出され，その度に，条件判定における比較演算と論理演算の評価が，あわせて最大でク回行われる。ここでの計算量が少なくなるようにプログラムを改修することで，処理速度を向上させることができる可能性がある。
画像の情報量を落として画像ファイルのサイズを小さくしたり，モノクロの液晶画面に画像を表示させたりする際に，減色アルゴリズムを用いた画像変換を行うことがある。誤差拡散法は減色アルゴリズムの一つである。誤差拡散法を用いて，階調ありのモノクロ画像を，黒と白だけを使ったモノクロ2値の画像に画像変換した例を図1に示す。
階調ありのモノクロ画像の場合は，各ピクセルが色の濃淡をもつことができる。濃淡は輝度で表す。輝度0のとき色は黒に，輝度が最大になると色は白になる。モノクロ2値の画像は，輝度が0か最大かの2値だけを使った画像である。
画像を構成するピクセルの輝度は，1ピクセルの輝度を8ビットで表す場合，0～255の値を取ることができる。0が黒で，255が白を表す。誤差拡散法では，次の二つの処理をピクセルごとに行うことで減色を行う。
- 変換前のピクセルについて，白に近い場合は輝度を255，黒に近い場合は輝度を0としてモノクロ2値化し，その際の輝度の差分を評価し，輝度の誤差Dとする。
例えば，変換前のピクセルの輝度が223の場合，変換後の輝度を255とし，輝度の誤差Dは，223－255から，－32である。 - 事前に定義した誤差拡散のパターンに従って，評価した誤差Dを周囲のピクセル(以下，拡散先という)に拡散させる。
誤差拡散法を用いて減色するプログラムを作成した。プログラム中で使用する主な変数，定数及び配列を表1に，作成したプログラムを図5に示す。
ピクセルを処理する順番を，Y座標ごとに逆向きにすることで，誤差拡散の方向の偏りを減らし，画質を改善することができる。
- Y座標が奇数の場合：ピクセルを左から順に処理する。
- Y座標が偶数の場合：ピクセルを右から順に処理する。
図5中の③の箇所では，誤差を拡散させる先のピクセルが画像の範囲の外側にならないように制御している。このような処理をクリッピングという。
③のif文は，プログラムの終了までにキ回呼び出され，その度に，条件判定における比較演算と論理演算の評価が，あわせて最大でク回行われる。ここでの計算量が少なくなるようにプログラムを改修することで，処理速度を向上させることができる可能性がある。
設問1
図4の左上から3ピクセル目について処理した後の状態から処理を進め，太枠で示されたピクセルの一つ右隣のピクセルを処理した後の変換後輝度配列について，(1)，(2)に答えよ。
- 減色処理の結果のピクセル(上から1行目，左から4列目の要素)の色を，白か黒で答えよ。
- (1)のピクセルの処理後に，そのピクセルの下のピクセル(上から2行目，左から4列目の要素)に入る輝度の値を整数で答えよ。
解答入力欄
解答例・解答の要点
- 黒
- 33
解説
- 図3の減色処理の手順に従って、図4の左上から4ピクセル目に対して減色処理を行ったあとの、このピクセルが白か黒かを考えます。
- 手順2より、変換前画像から4ピクセル目の輝度を取得します。今回の場合は 35 です。
- 手順3より、Fに"変換前画像の輝度＋変換後輝度配列の同じ要素の値"を求めます。変換前画像の輝度は35、変換後輝度配列の同じ要素の値は49ですので、「F＝35＋49＝84」となります。
- 手順4より、Fの値から変換後輝度配列の輝度と、誤差の値Dを決定します。
今回は F＝84 であり、128より小さいため、変換後輝度配列の輝度を0、誤差の値 D＝F＝84 に設定します。
∴黒 - (1)のピクセルの処理後に、そのピクセルの下のピクセル(上から2行目、左から4列目の要素)に入る輝度の値を考えます。(1)の続きとして、減色処理を行っていきます。
手順5より、誤差拡散のパターンに従って、拡散先の要素に加算します。
図2より下のピクセルへの拡散は、D×5÷16 で計算できることがわかります。誤差の値Dは84なので拡散する値は「84×5÷16＝26.25」、問題文には「拡散する誤差の値は整数とし，小数点以下は切り捨てる」とあるので、小数点以下を切り捨てた「26.25→26」が実際に拡散する値となります。
この値を変換後輝度配列の同じ要素に加算するので、下のピクセル(上から2行目、左から4列目の要素)の輝度は「7＋26＝33」になります。
∴33
設問2
図5中のア～ウに入れる適切な字句を答えよ。
解答入力欄
- ア：
- イ：
- ウ：
解答例・解答の要点
- ア：bmpFrom[x,y] + bmpTo[x,y]
- イ：fが128以上
- ウ：bmpTo[px,py] + (d * ratio[c] / denominator)
解説
〔アについて〕
ピクセルごとに繰り返す処理のうち最初の処理であることと代入先の変数が f であることから、図3中の手順3の、変換前画像の輝度と、変換後輝度配列の同じ要素の値をFに求める処理に相当する部分であると判断できます。
表1の説明より、変換前画像の輝度は配列 bmpFrom[] に、変換後画像の輝度は配列 bmpTo[] に格納されていて、配列の添字は[X座標, Y座標]と指定することがわかります。ループ変数 x には現在処理中のX座標が、同じく y にはY座標が格納されているので、変換前画像の輝度は bmpFrom[x,y]、それに対応する変換後輝度配列は bmpTo[x,y] で参照できます。
したがって、[ア]には上記2つの輝度を合計を求める bmpFrom[x,y] + bmpTo[x,y] という式が当てはまります。
∴ア＝bmpFrom[x,y] + bmpTo[x,y]
〔イについて〕
if文の真偽にかかわらず、誤差を表すと思われる変数 d に値を設定していることと変換後画像の輝度を更新していることから、図3中の手順4の処理に相当する部分であると判断できます。
[イ]の式が真と評価されるときには、誤差の値dを f－255 に、変換後画像の輝度を255に設定していますが、これは手順4中の「Fの値(輝度の合計)が128以上なら変換後輝度配列の輝度を255とし、誤差の値DをF-255とする」処理に該当します。よって、[イ]には fが128以上 という条件式が当てはまります。
∴イ＝fが128以上
〔ウについて〕
プログラムの11～18行目は、手順5に該当し、誤差拡散パターンに定義された割合に従って配分して拡散先の要素に加算する処理です。[ウ]には拡散先の要素を更新する値が入ります。
誤差拡散の処理を確認すると、拡散後の変換後輝度の値は以下の要領で求めることになります。
拡散後の変換後輝度＝拡散前の変換後輝度＋拡散する誤差の値
拡散する誤差の値＝切捨て(誤差×誤差拡散パターン)
各変数は以下のように参照できます。
∴ウ＝bmpTo[px, py] + d × ratio[c] / denominator
この穴埋めについては疑問があります。
まず1点目ですが、公式解答には()が付いていますが、疑似言語においても乗除演算は加減演算に優先するのでなぜ付いているのか不明です。
2点目は、仕様上は拡散する誤差の値は整数値ということになっていますが、整数同士の"/"の結果が整数になるのはC言語やJava等の特定のプログラム言語に限られるので、整数値が格納される保証はないように思えます。疑似言語の細かな仕様について定義がない以上、切捨てを行う関数を用意するべきだったと思います。
3点目ですが、演算子として*・/を使うのか×・÷を使うのかが判断できません。乗算については図7中に記載があるため"*"とわかりますが、除算の余りは"%"でなく"mod"だし、統一感がなく受験者に不親切です。疑似言語の仕様書の公開を強く望みます。
最後となりますが、配列の添字が0始まりなのか1始まりなのかの記載がありません。他の年度のプログラミング問題では記載があるので、記載するのを忘れたのだと思われます。
※かなり辛辣に指摘しましたが私が見落としているだけかもしれません。もしそうだったらご指摘くださると助かります。
ピクセルごとに繰り返す処理のうち最初の処理であることと代入先の変数が f であることから、図3中の手順3の、変換前画像の輝度と、変換後輝度配列の同じ要素の値をFに求める処理に相当する部分であると判断できます。
表1の説明より、変換前画像の輝度は配列 bmpFrom[] に、変換後画像の輝度は配列 bmpTo[] に格納されていて、配列の添字は[X座標, Y座標]と指定することがわかります。ループ変数 x には現在処理中のX座標が、同じく y にはY座標が格納されているので、変換前画像の輝度は bmpFrom[x,y]、それに対応する変換後輝度配列は bmpTo[x,y] で参照できます。
したがって、[ア]には上記2つの輝度を合計を求める bmpFrom[x,y] + bmpTo[x,y] という式が当てはまります。
∴ア＝bmpFrom[x,y] + bmpTo[x,y]
〔イについて〕
if文の真偽にかかわらず、誤差を表すと思われる変数 d に値を設定していることと変換後画像の輝度を更新していることから、図3中の手順4の処理に相当する部分であると判断できます。
[イ]の式が真と評価されるときには、誤差の値dを f－255 に、変換後画像の輝度を255に設定していますが、これは手順4中の「Fの値(輝度の合計)が128以上なら変換後輝度配列の輝度を255とし、誤差の値DをF-255とする」処理に該当します。よって、[イ]には fが128以上 という条件式が当てはまります。
∴イ＝fが128以上
〔ウについて〕
プログラムの11～18行目は、手順5に該当し、誤差拡散パターンに定義された割合に従って配分して拡散先の要素に加算する処理です。[ウ]には拡散先の要素を更新する値が入ります。
誤差拡散の処理を確認すると、拡散後の変換後輝度の値は以下の要領で求めることになります。
拡散後の変換後輝度＝拡散前の変換後輝度＋拡散する誤差の値
拡散する誤差の値＝切捨て(誤差×誤差拡散パターン)
各変数は以下のように参照できます。
- 誤差 … d
- 誤差拡散パターンの分母 … denominator
- 誤差拡散パターンの分子 … ratio[c]
- 拡散処理中の配列要素 … bmpTo[px, py]
- 拡散する誤差の値
- d × ratio[c] / denominator
- 拡散後の変換後輝度
- bmpTo[px, py] + d × ratio[c] / denominator
∴ウ＝bmpTo[px, py] + d × ratio[c] / denominator
この穴埋めについては疑問があります。
まず1点目ですが、公式解答には()が付いていますが、疑似言語においても乗除演算は加減演算に優先するのでなぜ付いているのか不明です。
2点目は、仕様上は拡散する誤差の値は整数値ということになっていますが、整数同士の"/"の結果が整数になるのはC言語やJava等の特定のプログラム言語に限られるので、整数値が格納される保証はないように思えます。疑似言語の細かな仕様について定義がない以上、切捨てを行う関数を用意するべきだったと思います。
3点目ですが、演算子として*・/を使うのか×・÷を使うのかが判断できません。乗算については図7中に記載があるため"*"とわかりますが、除算の余りは"%"でなく"mod"だし、統一感がなく受験者に不親切です。疑似言語の仕様書の公開を強く望みます。
最後となりますが、配列の添字が0始まりなのか1始まりなのかの記載がありません。他の年度のプログラミング問題では記載があるので、記載するのを忘れたのだと思われます。
※かなり辛辣に指摘しましたが私が見落としているだけかもしれません。もしそうだったらご指摘くださると助かります。
設問3
図6，図7中のエ～カに入れる適切な字句を答えよ。
解答入力欄
- エ：
- オ：
- カ：
解答例・解答の要点
- エ：y
- オ：2
- カ：width - tx + 1
解説
〔エ、オについて〕
問題文の〔画質向上のための改修〕では、以下の記述があります。
ある値Xが奇数か偶数かは、Xを2で割った余りで判定できます。X mod 2 が0ならばXは偶数、X mod 2 が1ならばXは奇数となります。現在処理中のY座標は変数yに格納されているので、[エ]には y、[オ]には 2 が当てはまります。
∴エ＝y
オ＝2
〔カについて〕
Y座標が偶数の場合はピクセルを右から順に処理するため、tx が1のときには x は width、tx が2のときには x は width-1、…、tx が width のときには x は 1、というように右から tx 番目の位置に変換してあげる必要があります。
この関係を tx と width を使用して表すと「width - tx + 1」という式になります。したがって、[カ]には width - tx + 1 が入ります。
※ループの最初で x ← tx を行っているため、tx ではなく x でも問題ありません。また項の順序が入れ替わっていても問題ありません。
∴カ＝width - tx + 1
問題文の〔画質向上のための改修〕では、以下の記述があります。
- Y座標が奇数の場合：ピクセルを左から順に処理する。
- Y座標が偶数の場合：ピクセルを右から順に処理する。
ある値Xが奇数か偶数かは、Xを2で割った余りで判定できます。X mod 2 が0ならばXは偶数、X mod 2 が1ならばXは奇数となります。現在処理中のY座標は変数yに格納されているので、[エ]には y、[オ]には 2 が当てはまります。
∴エ＝y
オ＝2
〔カについて〕
Y座標が偶数の場合はピクセルを右から順に処理するため、tx が1のときには x は width、tx が2のときには x は width-1、…、tx が width のときには x は 1、というように右から tx 番目の位置に変換してあげる必要があります。
この関係を tx と width を使用して表すと「width - tx + 1」という式になります。したがって、[カ]には width - tx + 1 が入ります。
※ループの最初で x ← tx を行っているため、tx ではなく x でも問題ありません。また項の順序が入れ替わっていても問題ありません。
∴カ＝width - tx + 1
設問4
本文中のキ，クに入れる適切な字句を答えよ。
解答入力欄
- キ：
- ク：
解答例・解答の要点
- キ：height×width×ratioCount
- ク：7
解説
〔キについて〕
図5のプログラムは三重のforループ構造になっており、それぞれの部分は以下の回数繰り返されます。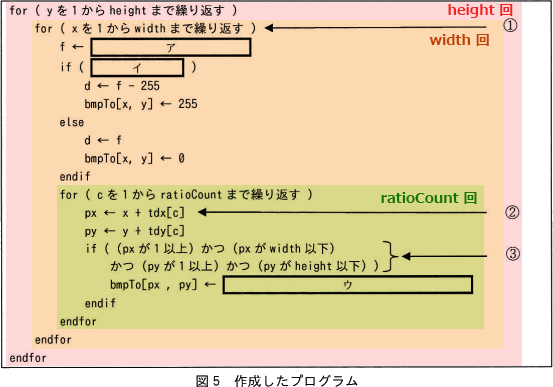
最も内部にある③の処理は合計で「height×width×ratioCount」回実行されることになります。
∴キ＝height×width×ratioCount
〔クについて〕
③の処理を比較演算と論理演算に分解し、演算の評価回数を求めます。比較演算とは項同士の値を比較している部分（ピンク）、論理演算とは真偽値(true or false)同士をAND演算やOR演算している部分（オレンジ）です。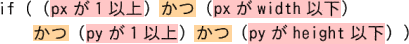
図のとおり、if文の真偽判定のために比較演算が4回、論理演算が3回行われるので評価回数の合計は7回です。
∴ク＝7
図5のプログラムは三重のforループ構造になっており、それぞれの部分は以下の回数繰り返されます。
∴キ＝height×width×ratioCount
〔クについて〕
③の処理を比較演算と論理演算に分解し、演算の評価回数を求めます。比較演算とは項同士の値を比較している部分（ピンク）、論理演算とは真偽値(true or false)同士をAND演算やOR演算している部分（オレンジ）です。
∴ク＝7
