応用情報技術者過去問題 平成22年春期 午後問2
⇄問題文と設問を画面2分割で開く⇱問題PDF問2 プログラミング
アプリケーションで使用するデータ構造とアルゴリズムに関する次の記述を読んで,設問1~4に答えよ。
PCのデスクトップ上の好きな位置に付箋(ふせん)を配置できるアプリケーションの実行イメージを図1に,付箋1枚のデータイメージを図2に示す。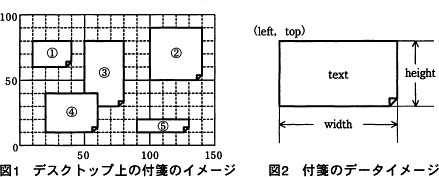 複数の付箋データを管理する方法として,配列と双方向リスト(以下,リストという)のいずれがよいかを検討することにした。そこで,図1の付箋③のようにほかの付箋の背後にある付箋を一番手前に移動するアルゴリズムを,配列とリストそれぞれで実装して比較検討する。使用する構造体,配列,定数,変数及び関数を表に示す。また,図1の付箋①~⑤を順番に,配列及びリストにそれぞれ格納した際のイメージを図3,4に示す。
複数の付箋データを管理する方法として,配列と双方向リスト(以下,リストという)のいずれがよいかを検討することにした。そこで,図1の付箋③のようにほかの付箋の背後にある付箋を一番手前に移動するアルゴリズムを,配列とリストそれぞれで実装して比較検討する。使用する構造体,配列,定数,変数及び関数を表に示す。また,図1の付箋①~⑤を順番に,配列及びリストにそれぞれ格納した際のイメージを図3,4に示す。
なお,配列及びリストの末尾に近い付箋データほど,デスクトップ上の手前に表示される。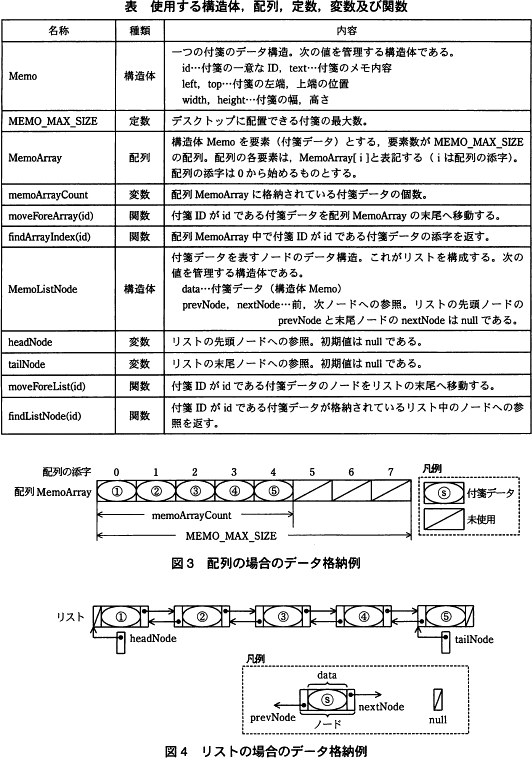 構造体の要素は"."を使った表記で表す。"."の左には,構造体を表す変数又は構造体を参照する変数を書く。"."の右には,要素の名前を書く。配列の場合,図3の付箋⑤のメモ内容は MemoArray[4].text,また,リストの場合,図4の付箋②のIDは headNode.nextNode.data.id と表記できる。
構造体の要素は"."を使った表記で表す。"."の左には,構造体を表す変数又は構造体を参照する変数を書く。"."の右には,要素の名前を書く。配列の場合,図3の付箋⑤のメモ内容は MemoArray[4].text,また,リストの場合,図4の付箋②のIDは headNode.nextNode.data.id と表記できる。
〔関数 moveForeArray〕
関数 moveForeArray の処理手順を次の(1)~(4)にそのプログラムを図5に示す。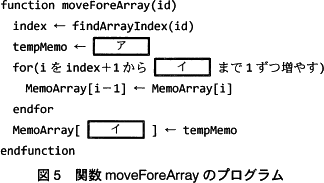 〔関数 moveForeList〕
〔関数 moveForeList〕
関数 moveForeList の処理手順を次の(1)~(4)に処理手順中の(3)(ⅱ)及び(4)の操作を図6に示す。また,関数 moveForeLis tのプログラムを図7に示す。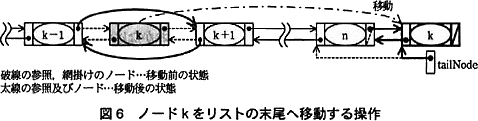
 〔二つのアルゴリズムに関する考察〕
〔二つのアルゴリズムに関する考察〕
まず,時間計算量について考える。配列の場合,末尾へ移動する要素より後のすべての要素をずらす必要が生じる。この処理の計算量はオである。リストの場合,末尾へ移動する付箋データの位置にかかわらず,少数の参照の変更だけでデータ同士の相対的な位置関係を簡単に変えられる。この処理の計算量はカである。
次に,必要な領域の大きさについて考える。付箋データ1個当たりの領域の必要量は,配列の方が小さい。リストは参照を入れる場所を余分に必要とする。しかし,全体で必要とする領域は,配列の場合,キしておかなければならない。リストの場合,配置されている付箋データの個数分だけ領域を確保すればよい。
PCのデスクトップ上の好きな位置に付箋(ふせん)を配置できるアプリケーションの実行イメージを図1に,付箋1枚のデータイメージを図2に示す。

なお,配列及びリストの末尾に近い付箋データほど,デスクトップ上の手前に表示される。

〔関数 moveForeArray〕
関数 moveForeArray の処理手順を次の(1)~(4)にそのプログラムを図5に示す。
- 配列中の付箋IDが id である付箋データの添字を取得する。
- 配列中の(1)で取得した位置の付箋データを一時変数へ退避する。
- 配列中の(1)で取得した位置の次から配列の最後の付箋データがある位置までの付箋データを一つずつ前へずらす。
- 配列中の最後の付箋データがあった位置へ(2)で退避した付箋データを代入する。

関数 moveForeList の処理手順を次の(1)~(4)に処理手順中の(3)(ⅱ)及び(4)の操作を図6に示す。また,関数 moveForeLis tのプログラムを図7に示す。
- リストから,付箋IDが id である付箋データをもつノードへの参照を取得する。
- (1)で取得したノード(ノードk)が末尾ノードの場合,処理を終了する。
- ノードkが先頭ノードの場合は(ⅰ)を,そうでない場合は(ⅱ)を実行する。ここで,ノードkの次ノードをノードk+1,前ノードをノードk-1と呼ぶ。
- リストの先頭ノードへの参照をノードk+1への参照に変更し,ノードk+1中の前ノードへの参照をnullに変更する。
- ノードk-1中の次ノードへの参照をノードk+1への参照に変更し,ノードk+1中の前ノードへの参照をノードk-1への参照に変更する。
- リストの末尾ノード(ノードn)中の次ノードへの参照をノードkへの参照に,ノードk中の前ノードへの参照をノードnへの参照に変更する。ノードk中の次ノードへの参照をnullに,リストの末尾ノードへの参照(tailNode)をノードkへの参照に変更する。


まず,時間計算量について考える。配列の場合,末尾へ移動する要素より後のすべての要素をずらす必要が生じる。この処理の計算量はオである。リストの場合,末尾へ移動する付箋データの位置にかかわらず,少数の参照の変更だけでデータ同士の相対的な位置関係を簡単に変えられる。この処理の計算量はカである。
次に,必要な領域の大きさについて考える。付箋データ1個当たりの領域の必要量は,配列の方が小さい。リストは参照を入れる場所を余分に必要とする。しかし,全体で必要とする領域は,配列の場合,キしておかなければならない。リストの場合,配置されている付箋データの個数分だけ領域を確保すればよい。
設問1
図1の付箋①~⑤を格納した図3の配列及び図4のリストについて,(1),(2)に答えよ。
- 配列に格納されている,付箋①の高さ20を求める適切な式を答えよ。
- tailNode.prevNode.data.heightの値を答えよ。
解答入力欄
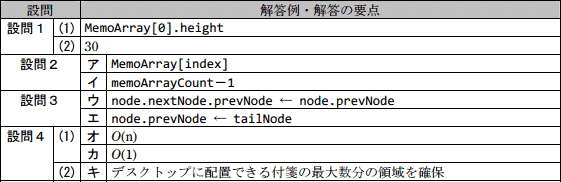
解答例・解答の要点
- MemoArray[0].height
- 30
解説
- 図3より、配列で実装する場合、付箋データは配列 MemoArray に格納されることがわかります。付箋①に対応するのは MemoArray[0] です。
ここで表の MemoArray の説明文より、配列 MemoArray の要素は構造体 Memo であることがわかります。構造体 Memo の説明文より、付箋の高さは要素 height で管理されていることがわかります。
構造体の要素は「構造体を表す変数.要素名」で参照できます。MemoArray[0] の height を参照したいので、解答は「MemoArray[0].height」になります。
∴MemoArray[0].height - tailNode.prevNode.data.height の左から順に、それぞれが何を表すのかを読み解いていきましょう。
- tailNode
- 図4より、tailNode はリストの末尾のノード、つまり付箋⑤に対応するノードであることがわかります。
- prevNode
- 図4より、prevNode はあるノードの一つ前のノードになります。今回の例では付箋⑤の一つ前、すなわち付箋④に対応するノードであることがわかります。
- data
- 表の MemoListNode の説明文より、data は構造体 Memo で作られた付箋データです。
- height
- 表の構造体Memoの説明文より、heightは付箋の高さです。
図1を確認すると、付箋④の上端の縦座標は40、下端の縦座標は10ですから、「40-10=30」より高さは30です。
∴30
設問2
図5中のア,イに入れる適切な字句を答えよ。
解答入力欄
- ア:
- イ:
解答例・解答の要点
- ア:MemoArray[index]
- イ:MemoArrayCount-1
解説
関数 moveForeArray の処理手順と図5のコードとの対応を考えます。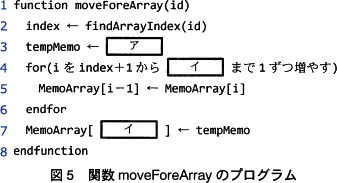 〔アについて〕
〔アについて〕
2行目は、関数 moveForeArray の処理手順(1)と対応しています。よって、[ア]が含まれる3行目は処理手順(2)の処理に対応すると推測できます。
まず、処理手順(2)の「配列中の(1)で取得した位置の付箋データ」について考えます。「処理手順(1)で取得した位置」は、2行目で変数 index に格納されていることから、その付箋データは「MemoArray[index]」です。
次に、処理手順(2)の「付箋データを一時変数へ退避する」について考えます。3行目を見ると、代入先となっている変数 tempNode が退避先の一時変数であり、代入元である[ア]は付箋データを表すことがわかります。
以上より、解答は「MemoArray[index]」となります。
∴ア=MemoArray[index]
〔イについて〕
4~6行目は処理手順の(3)と対応し、図5の7行目は処理手順(4)と対応します。
[イ]が記載されている図5の4行目・7行目を見ると、[イ]は配列 MemoArray の添字となる値であることがわかります。
処理手順(3)では、取得した位置の次の要素から最後の要素までを一つずつ前にずらし、処理手順では配列の末尾の位置に取得した要素を代入します。つまり、[イ]には「配列の末尾要素の添字」を表す式が入ることになります。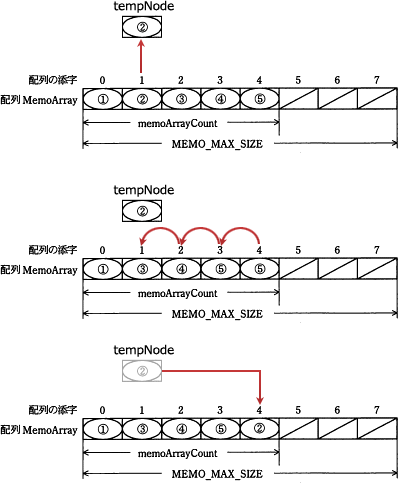 「配列の末尾要素の添字」を導出するには、配列の要素数がわかればよいです。表より、配列 MemoArray の要素数は変数 memoArrayCount で参照できることがわかります。配列 MemoArray の添字が0から始まることに注意すると、末尾要素の添字は「memoArrayCount-1」と表せます。これが解答となります。
「配列の末尾要素の添字」を導出するには、配列の要素数がわかればよいです。表より、配列 MemoArray の要素数は変数 memoArrayCount で参照できることがわかります。配列 MemoArray の添字が0から始まることに注意すると、末尾要素の添字は「memoArrayCount-1」と表せます。これが解答となります。
∴イ=MemoArrayCount-1

2行目は、関数 moveForeArray の処理手順(1)と対応しています。よって、[ア]が含まれる3行目は処理手順(2)の処理に対応すると推測できます。
まず、処理手順(2)の「配列中の(1)で取得した位置の付箋データ」について考えます。「処理手順(1)で取得した位置」は、2行目で変数 index に格納されていることから、その付箋データは「MemoArray[index]」です。
次に、処理手順(2)の「付箋データを一時変数へ退避する」について考えます。3行目を見ると、代入先となっている変数 tempNode が退避先の一時変数であり、代入元である[ア]は付箋データを表すことがわかります。
以上より、解答は「MemoArray[index]」となります。
∴ア=MemoArray[index]
〔イについて〕
4~6行目は処理手順の(3)と対応し、図5の7行目は処理手順(4)と対応します。
[イ]が記載されている図5の4行目・7行目を見ると、[イ]は配列 MemoArray の添字となる値であることがわかります。
処理手順(3)では、取得した位置の次の要素から最後の要素までを一つずつ前にずらし、処理手順では配列の末尾の位置に取得した要素を代入します。つまり、[イ]には「配列の末尾要素の添字」を表す式が入ることになります。

∴イ=MemoArrayCount-1
設問3
図7中のウ,エに入れる適切な字句を答えよ。
解答入力欄
- ウ:
- エ:
解答例・解答の要点
- ウ:node.nextNode.prevNode ← node.prevNode
- エ:node.prevNode ← tailNode
解説
関数 moveForeList の処理手順と図7のコードとの対応を考えます。 [処理手順(1)について]
[処理手順(1)について]
処理手順(1)は2行目と対応しています。
[処理手順(2)について]
処理手順(2)は「末尾ノードの場合」の処理です。
4行目のコメント「//末尾ノードの場合」より、3~6行目が対応する処理とわかります。最前面に表示したい要素は既に末尾にありますから何らすることはありません。
[処理手順(3)について]
処理手順(3)は「先頭ノードの場合」「そうでない場合」とで分岐する処理です。
8行目のコメント「// 先頭ノードの場合」および12行目のコメント「// 先頭ノード以外の場合」より、7~15行目が対応する処理とわかります。
[処理手順(4)について]
処理手順(4)は処理手順(1)~(3)に対応していない残りの部分、すなわち16行目~19行目が対応する処理とわかります。
以上を踏まえて空欄に入る字句を考えます。
〔ウについて〕
13~14行目の処理は、12行目のコメント「// 先頭ノード以外の場合」より、処理手順(3)(ⅱ)に対応する処理です。
処理手順(3)の文中に出てくる「ノードk」についてですが、処理手順(2)に「(1)で取得したノード(ノードk)」とあること、および2行目で取得したノードが変数 node に代入されていることから、「ノードk」は変数 node として表されていることがわかります。
「ノードk」が変数 node であることから、13行目の処理を文章で表すと、『ノードkの前ノード』の次ノードへの参照を、『ノードkの次ノード』にする、となります。
「ノードkの前ノード」は「ノードk-1」、「ノードkの次ノード」は「ノードk+1」と解釈できるので、13行目の処理は処理手順(3)(ⅱ)の前半の処理に対応していることになります。図6中では以下の参照付け替え処理に当たります。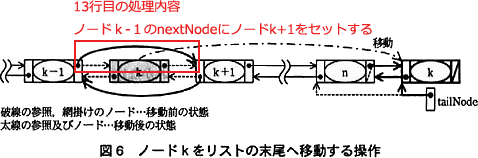 したがって、[ウ]には処理手順(3)(ⅱ)の後半、「ノードk+1中の前ノードへの参照をノードk-1への参照に変更する」処理が入ります。13行目のように、「ノードk+1」は node.nextNode、「ノードk-1」は node.prevNode で表せますから、解答は「node.nextNode.prevNode ← node.nextNode」となります。
したがって、[ウ]には処理手順(3)(ⅱ)の後半、「ノードk+1中の前ノードへの参照をノードk-1への参照に変更する」処理が入ります。13行目のように、「ノードk+1」は node.nextNode、「ノードk-1」は node.prevNode で表せますから、解答は「node.nextNode.prevNode ← node.nextNode」となります。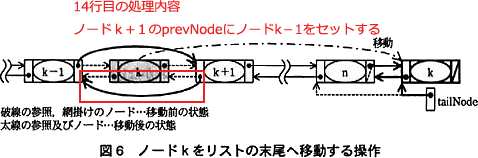 ∴ウ=node.nextNode.prevNode ← node.prevNode
∴ウ=node.nextNode.prevNode ← node.prevNode
〔エについて〕
処理手順(4)と照らし合わせて、[エ]がどの処理に該当するか考えます。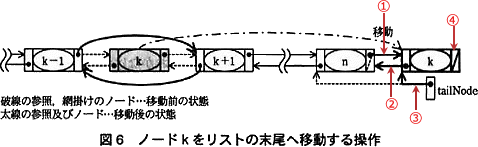 16行目は、処理手順(4)のうち「リストの末尾ノード(ノードn)中の次ノードへの参照をノードkへの参照に」する処理です(①)。
16行目は、処理手順(4)のうち「リストの末尾ノード(ノードn)中の次ノードへの参照をノードkへの参照に」する処理です(①)。
18行目は、処理手順(4)のうち「ノードk中の次ノードへの参照をnullに」する処理です(④)。
19行目は、処理手順(4)のうち「リストの末尾ノードへの参照(tailNode)をノードkへの参照に変更する」処理です(③)。
よって、[エ]は処理手順(4)のうち上記のいずれにも含まれない「ノードk中の前ノードへの参照をノードnへの参照に変更する」処理(②)になります。ここで「ノードn」は、処理手順(4)の文章から「リストの末尾ノード」であり、tailNode と表せます。また、「ノードk」は[ウ]でも解説したように変数 node で表せます。
したがって、解答は「node.prevNode ← tailNode」となります。
∴エ=node.prevNode ← tailNode

処理手順(1)は2行目と対応しています。
[処理手順(2)について]
処理手順(2)は「末尾ノードの場合」の処理です。
4行目のコメント「//末尾ノードの場合」より、3~6行目が対応する処理とわかります。最前面に表示したい要素は既に末尾にありますから何らすることはありません。
[処理手順(3)について]
処理手順(3)は「先頭ノードの場合」「そうでない場合」とで分岐する処理です。
8行目のコメント「// 先頭ノードの場合」および12行目のコメント「// 先頭ノード以外の場合」より、7~15行目が対応する処理とわかります。
[処理手順(4)について]
処理手順(4)は処理手順(1)~(3)に対応していない残りの部分、すなわち16行目~19行目が対応する処理とわかります。
以上を踏まえて空欄に入る字句を考えます。
〔ウについて〕
13~14行目の処理は、12行目のコメント「// 先頭ノード以外の場合」より、処理手順(3)(ⅱ)に対応する処理です。
処理手順(3)の文中に出てくる「ノードk」についてですが、処理手順(2)に「(1)で取得したノード(ノードk)」とあること、および2行目で取得したノードが変数 node に代入されていることから、「ノードk」は変数 node として表されていることがわかります。
「ノードk」が変数 node であることから、13行目の処理を文章で表すと、『ノードkの前ノード』の次ノードへの参照を、『ノードkの次ノード』にする、となります。
「ノードkの前ノード」は「ノードk-1」、「ノードkの次ノード」は「ノードk+1」と解釈できるので、13行目の処理は処理手順(3)(ⅱ)の前半の処理に対応していることになります。図6中では以下の参照付け替え処理に当たります。


〔エについて〕
処理手順(4)と照らし合わせて、[エ]がどの処理に該当するか考えます。

18行目は、処理手順(4)のうち「ノードk中の次ノードへの参照をnullに」する処理です(④)。
19行目は、処理手順(4)のうち「リストの末尾ノードへの参照(tailNode)をノードkへの参照に変更する」処理です(③)。
よって、[エ]は処理手順(4)のうち上記のいずれにも含まれない「ノードk中の前ノードへの参照をノードnへの参照に変更する」処理(②)になります。ここで「ノードn」は、処理手順(4)の文章から「リストの末尾ノード」であり、tailNode と表せます。また、「ノードk」は[ウ]でも解説したように変数 node で表せます。
したがって、解答は「node.prevNode ← tailNode」となります。
∴エ=node.prevNode ← tailNode
設問4
〔二つのアルゴリズムに関する考察〕について,(1),(2)に答えよ。
- 本文中のオ,カに入れる適切な字句をO記法で答えよ。
なお,配列及びリスト中の付箋データの個数をnとし,関数 findArrayIndex 及び関数 findListNode の計算量は無視する。 - リストの場合,配置されている付箋データの個数分だけ領域を確保すればよいのに対し,配列の場合はどうしなければならないのか。キに入れる適切な字句を30字以内で答えよ。
解答入力欄
- オ:
- カ:
- キ:
解答例・解答の要点
- オ:O(n)
- カ:O(1)
- キ:デスクトップに配置できる付箋の最大数分の領域を確保 (25文字)
解説
- 〔オについて〕
時間計算量について問われているので、アルゴリズムの処理中で最も時間がかかる場所について考えます。
本文には「配列の場合,末尾へ移動する要素より後のすべての要素をずらす必要が生じる」とあります。この処理は図5でも繰り返し処理で実装されており、最も時間がかかる処理になります。
ここで、ずらす必要が生じる要素の数は、最小で0個、最大で「付箋データの個数-1」個分、つまりn-1個となります(設問4(1)の問題文より付箋データの個数をnとするため)。「末尾へ移動する要素」の位置は特に条件が記載されていないので、先頭から末尾まで偏りなく平均的に指定されると考えて良いです。
したがって、ずらす必要のある付箋データの個数は、平均して(n-1)/2個、計算量はnの大きさにほぼ比例することになります。
O記法では一番影響力が強い項以外を無視し係数も書かないので、計算量は線形時間、すなわち「O(n)」となります。
∴オ=O(n)
〔カについて〕
リストの場合のアルゴリズムである図7のプログラムには、繰り返し処理がありません。また、関数 findListNode の計算量を無視すると問題文にあるため、このアルゴリズムは定数回の計算で処理を終えることができます。
したがって、計算量は定数時間、すなわち「O(1)」となります。
∴カ=O(1) - 〔キについて〕
本文より、配列の「データの領域の確保」に関してリストと異なる特性を答えることになります。
JavaScriptやRubyなどで使われる配列は、宣言後も要素数を変更できます(これを動的配列といいます)。一方で、C言語やJavaで使われる通常の配列(静的配列といいます)は、一度宣言すると後から要素数を変更できません。
表の MemoArray の説明文を見ると、配列の要素数が定数 MEMO_MAX_SIZE で固定されているので、本問では動的配列でなく、静的配列を使ってあらかじめ領域を確保していると推測できます。
したがって解答としては「あらかじめ付箋データの最大数分の領域を確保しなければならない」というような内容を記述すればよいです。
∴キ=デスクトップに配置できる付箋の最大数分の領域を確保